本文主要是介绍李宏毅深度强化学习导论——演员-评论员,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
引言
本文主要介绍演员-评论员(Actor-Critic)算法。
Critic

给定Actor θ \theta θ,Critic评估当观测到 s s s(或进一步地采取行动 a a a)的好坏。
价值函数(Value function),记为 V θ ( s ) V^\theta(s) Vθ(s),就是一种Critic。
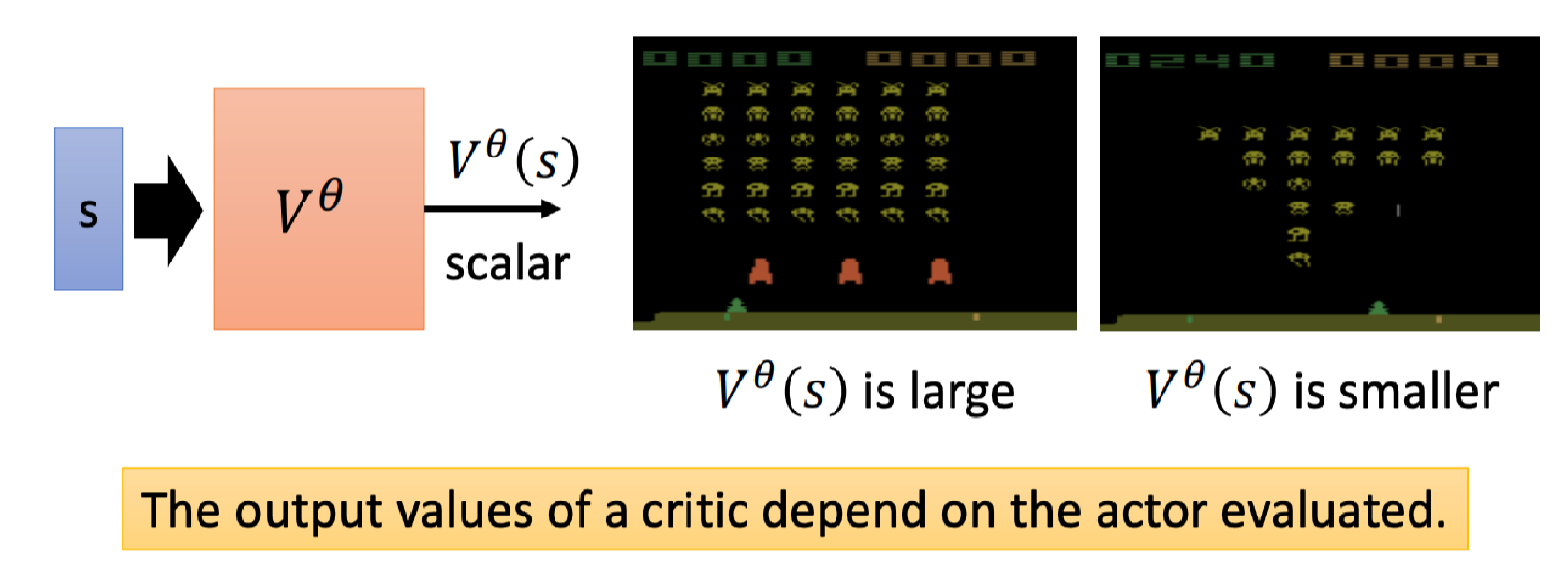
它的输入是现在的游戏画面,这里的上标 θ \theta θ表示它观察的对象是 θ \theta θ这个actor,输出是一个标量。这个标量表示当看到游戏画面 s s s,actor θ \theta θ接下来期望可以得到了折扣累积奖励: G 1 ′ = r 1 + γ r 2 + γ 2 r 3 + ⋯ G^\prime_1 = r_1 + \gamma r_2 + \gamma^2 r_3 + \cdots G1′=r1+γr2+γ2r3+⋯。
比如上图两个游戏画面中,左边有很多外星人,右边则相对少很多,因此左边估计的(价值)标量就会比右边大,当然前提是这个Actor足够厉害,不然没一会就挂了价值估计也会很低。
价值函数依赖于我们观察的Actor,同样的游戏画面不同的Actor应该要得到不同的价值。
那么如何估计价值函数?
我们可以训练一个Critic来估计价值函数,有两种常用的训练方法。
MC
第一种是基于Monte-Carlo(蒙特卡洛,MC)的方法。
它的原理是,让Actor θ \theta θ去和环境进行很多轮互动,然后就有很多的数据。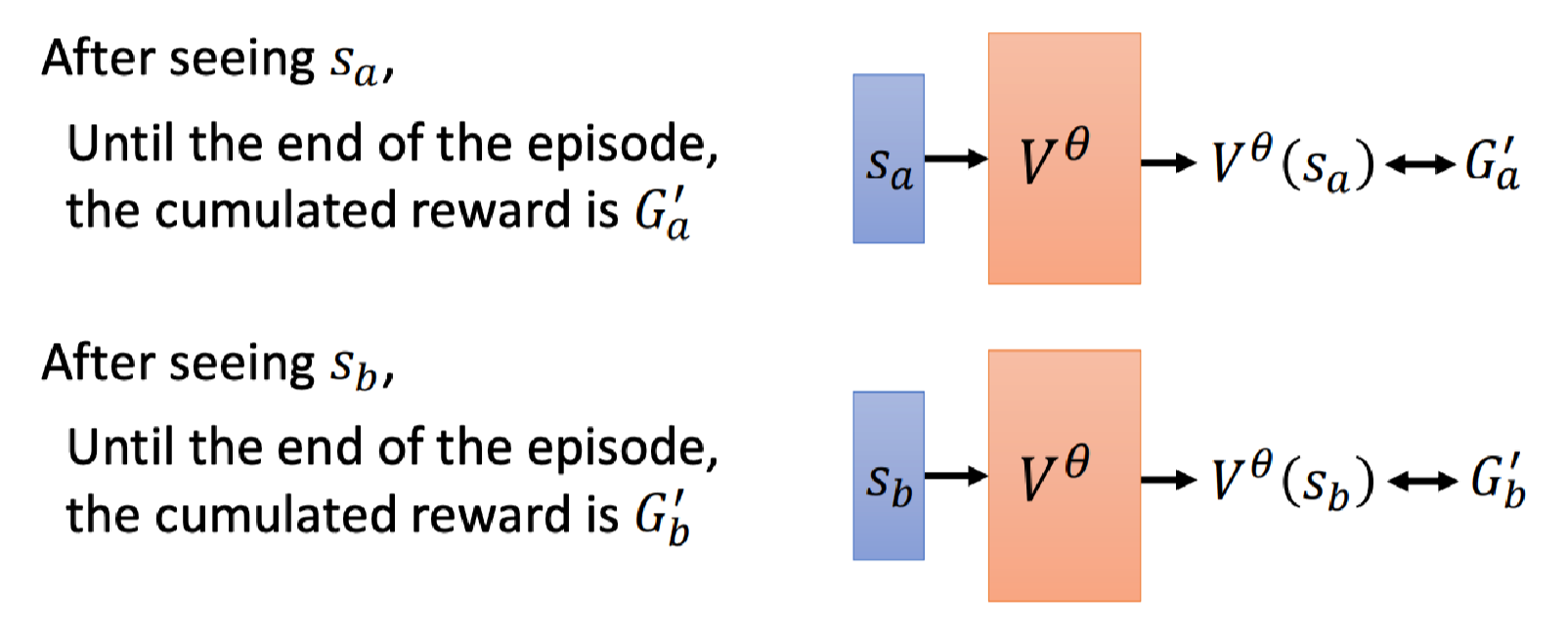
经过多轮游戏,我们知道看到状态 s a s_a sa,在这轮游戏结束折扣累积奖励会使 G a ′ G_a^\prime Ga′;看到状态 s b s_b sb,在这轮游戏结束折扣累积奖励会使 G b ′ G_b^\prime Gb′;
其实核心是计算期望,比如有很多轮游戏都看到了 s a s_a sa,然后计算它们的均值当成看到 s a s_a sa会后会得到的折扣累积奖励就好了。
那么我们让Critic看到 s a s_a sa或 s b s_b sb的输出分别与 G a ′ G_a^\prime Ga′或 G b ′ G_b^\prime Gb′越接近越好。
TD
另一种是时序差分(Temporal-difference,TD)方法。MC需要需要玩完整场游戏才能得到关于累积奖励的数据,而TD方法则不同。
只要有 s t , a t , r t , s t + 1 s_t,a_t,r_t,s_{t+1} st,at,rt,st+1的数据就好了,分别是当前状态、当前采取的行动、所获得的奖励、采取行动后跳到的下一个状态。
我们先来看 V θ ( s t ) V^\theta(s_t) Vθ(st)和 V θ ( s t + 1 ) V^\theta(s_{t+1}) Vθ(st+1)之间的关系:
V θ ( s t ) = r t + γ r t + 1 + γ 2 r t + 2 ⋯ V θ ( s t ) = r t + 1 + γ r t + 2 + γ 2 r t + 3 ⋯ (1) \begin{aligned} V^\theta(s_t) &= r_t + \gamma r_{t+1} + \gamma^2 r_{t+2} \cdots \\ V^\theta(s_t) &= r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} \cdots \\ \end{aligned} \tag 1 Vθ(st)Vθ(st)=rt+γrt+1+γ2rt+2⋯=rt+1+γrt+2+γ2rt+3⋯(1)
联立两个等式我们可以看出:
V θ ( s t ) = r t + γ V θ ( s t + 1 ) (2) V^\theta(s_t) = r_t + \gamma V^\theta(s_{t+1}) \tag 2 Vθ(st)=rt+γVθ(st+1)(2)
假设我们现在有这样的数据: s t , a t , r t , s t + 1 s_t,a_t,r_t,s_{t+1} st,at,rt,st+1。
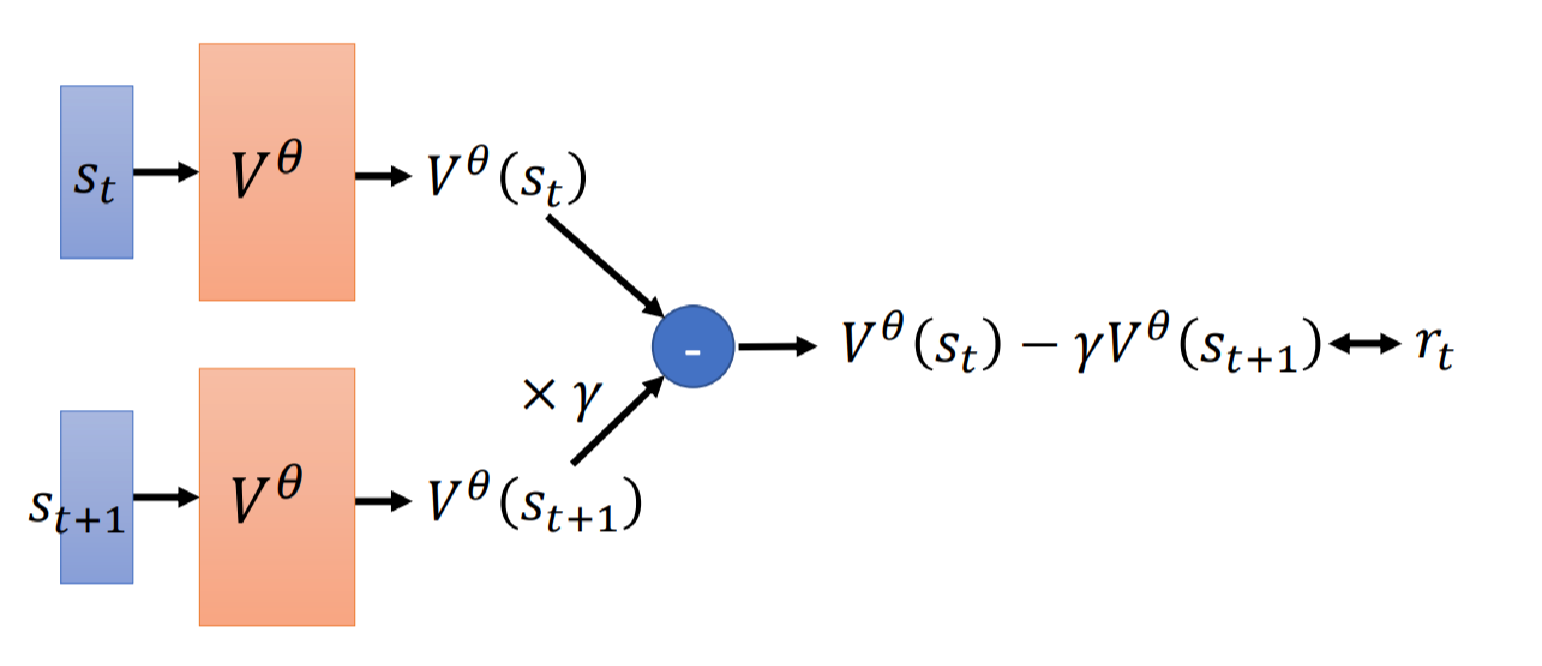
那么分别把 s t , s t + 1 s_t,s_{t+1} st,st+1代入价值函数中,分别得到 V θ ( s t ) V^\theta(s_t) Vθ(st)和 V θ ( s t + 1 ) V^\theta(s_{t+1}) Vθ(st+1),根据等式(2)前者减去 γ \gamma γ乘后者的值应该和 r t r_t rt尽量接近。
MC v.s. TD
假设Critic观察到下面8个episode的数据:

用MC和TD来观察,算出来的价值函数有可能不一样。
那么 V θ ( s b ) V^\theta(s_b) Vθ(sb)表示看到 s b s_b sb后actor θ \theta θ期望获得的折扣累积回报: 6 8 = 3 4 \frac{6}{8}=\frac{3}{4} 86=43,因为8次游戏里面有6次得到1分。
那 V θ ( s a ) V^\theta(s_a) Vθ(sa)怎么计算,根据MC方法有: 0 1 = 0 \frac{0}{1}=0 10=0;
根据TD方法(等式(2))有: V θ ( s a ) = r + V θ ( s b ) ⇒ 3 4 = 0 + V θ ( s b ) V^\theta(s_a) =r + V^\theta(s_b) \Rightarrow \frac{3}{4} = 0 + V^\theta(s_b) Vθ(sa)=r+Vθ(sb)⇒43=0+Vθ(sb), 所以 V θ ( s b ) = 3 4 V^\theta(s_b)=\frac{3}{4} Vθ(sb)=43。
可以看到这两种方法算出来的结果不一样,但从它们的角度来说,都是对的。
下面我们看Critic如何被用在训练Actor上。我们上篇文章说可以通过下图的方式来训练Actor:
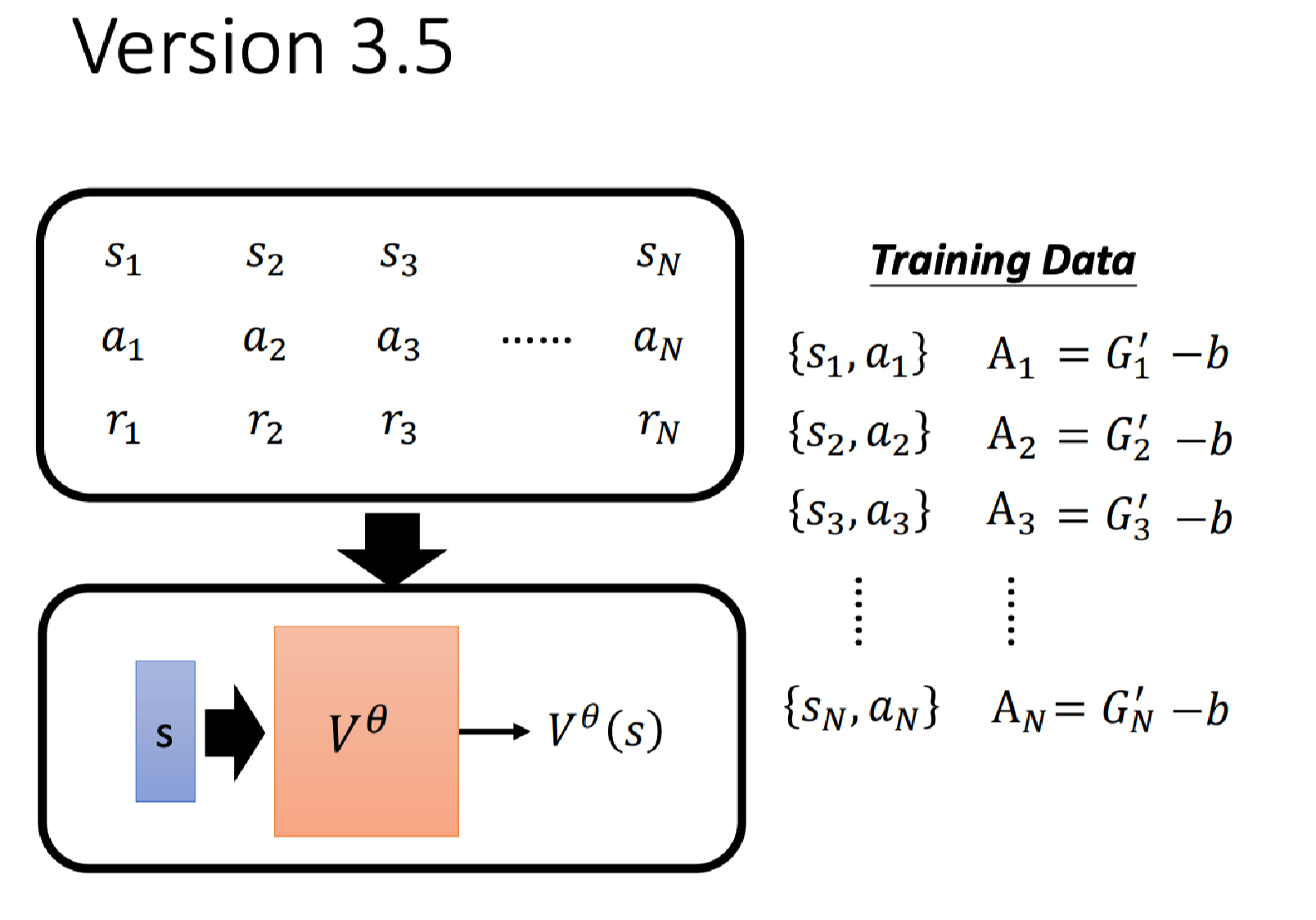
但我们留下来一个问题,即这个偏置 b b b的取值是多少?
这里有一个合理的取值,就是 V θ ( s ) V^\theta(s) Vθ(s)。
即我们根据同样的训练数据可以训练一个Critic,它可以衡量一个状态的期望累积奖励。所以:
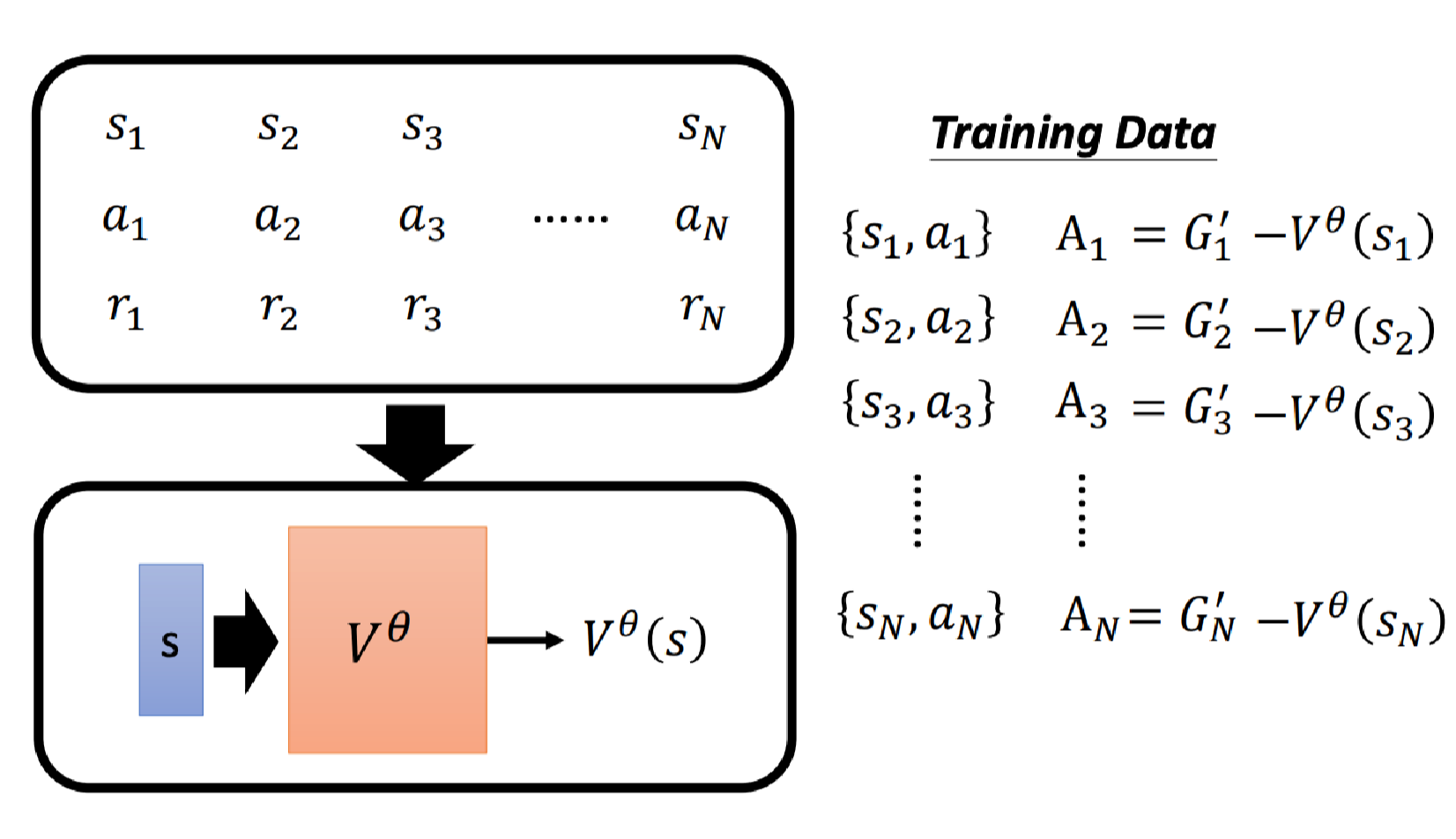
我们来理解下 V θ ( s t ) V^\theta(s_t) Vθ(st)代表什么意思。现在有 A t = G t ′ − V θ ( s t ) A_t = G_t^\prime - V^\theta(s_t) At=Gt′−Vθ(st)。

我们知道,根据概念是看到 s t s_t st后会得到的累积奖励期望值。但是要注意的是,看到 s t s_t st后,你的Actor不一定会执行 a t a_t at,因为在训练时Actor也要有随机性。
这样我们可以得到不同的累积奖励 G G G,平均起来就得到了 V θ ( s t ) V^\theta(s_t) Vθ(st)。
那么这里定义 G t ′ G_t^\prime Gt′为在 s t s_t st下执行 a t a_t at最后得到的累积奖励。
如果 A t > 0 A_t > 0 At>0代表 G t ′ > V θ ( s t ) G_t^\prime > V^\theta(s_t) Gt′>Vθ(st),表明动作 a t a_t at比(随机执行动作的)平均要好;否则如果 A t < 0 A_t < 0 At<0代表比平均要差。
但是仔细思考可能会发现哪里有点不对,这里 G t ′ G_t^\prime Gt′是一个样本的结果,而 V θ ( s t ) V^\theta(s_t) Vθ(st)是一个均值。
如果是拿均值减均值就得到了我们要了解的最后一个版本:
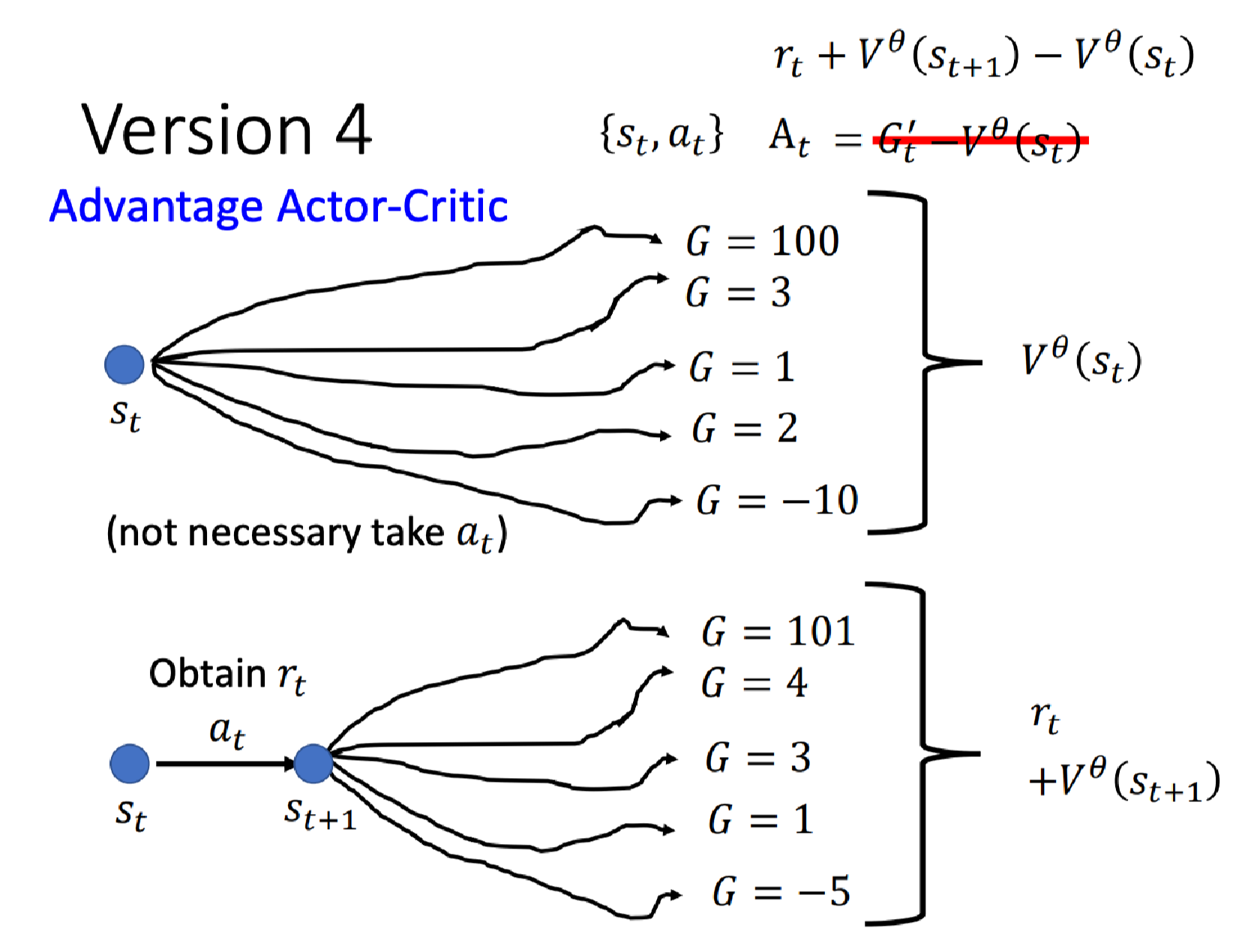
上一个版本我们是用 G t ′ − V θ ( s t ) G_t^\prime - V^\theta(s_t) Gt′−Vθ(st)来估计 A t A_t At。
现在变成了用均值,具体地,在 s t s_t st后执行动作 a t a_t at得到奖励 r t r_t rt,跳到状态 s t + 1 s_{t+1} st+1,然后在 s t + 1 s_{t+1} st+1处拿多个episode的均值计算出 V θ ( s t + 1 ) V^\theta(s_{t+1}) Vθ(st+1),或者说我们可以直接将 s t + 1 s_{t+1} st+1输入给我们的Critic就可以得到这个 V θ ( s t + 1 ) V^\theta(s_{t+1}) Vθ(st+1)。最后再加上 r t r_t rt就可以得到在 s t s_t st采取 a t a_t at后跳到 s t + 1 s_{t+1} st+1后会得到的期望累积奖励。
然后我们把 G t ′ G_t^\prime Gt′换成 r t + V θ ( s t + 1 ) r_t + V^\theta(s_{t+1}) rt+Vθ(st+1)得到
A t = r t + V θ ( s t + 1 ) − V θ ( s t ) A_t = r_t + V^\theta(s_{t+1}) - V^\theta(s_{t}) At=rt+Vθ(st+1)−Vθ(st)
这就是Advantage Actor-Critic(A2C)方法。
从算法描述我们可以看出Actor和Critic可以通过两个神经网络来模拟。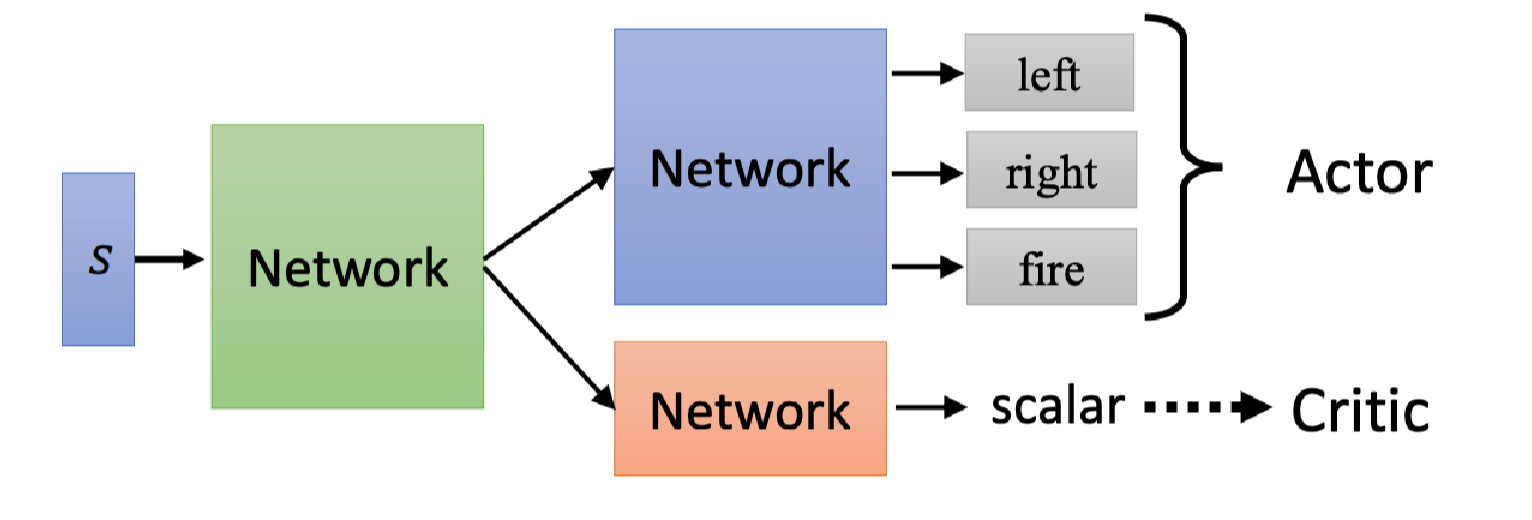
Actor看到游戏画面,输出要采取的动作分布;Critic看到游戏画面,输出这个Actor会得到的折扣累积奖励期望,是一个标量。
它们的输入是一样的,所以前几层的参数是可以共享的,比如输入是游戏画面时,那么前几层就是CNN网络。所以实际操作时我们可以设计成上图这样。绿色的网络代表CNN,用于游戏画面特征提取。
这篇关于李宏毅深度强化学习导论——演员-评论员的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



