统计学/机器学习入门（三）: 朴素贝叶斯Naïve Bayes及其决策边界，交叉验证

一）理论基础

不做过多介绍，NB（Naïve Bayes) 可用来分类，直接上公式：

P(H|E) = P(E|H) * P(H) / P(E)

二）举例说明

a)文本数据:

直接来个例子比较直观, 现在有这样一堆数据:

我们将通过过去的天气数据来判断 今天是否适合出去玩耍,然后今天的天气是这样:

这就是个很简单的0 1问题，play到底可不可以呢，于是我们就需要计算P(yes|E)和P(no|E)的概率，进行比较即可完成分类：

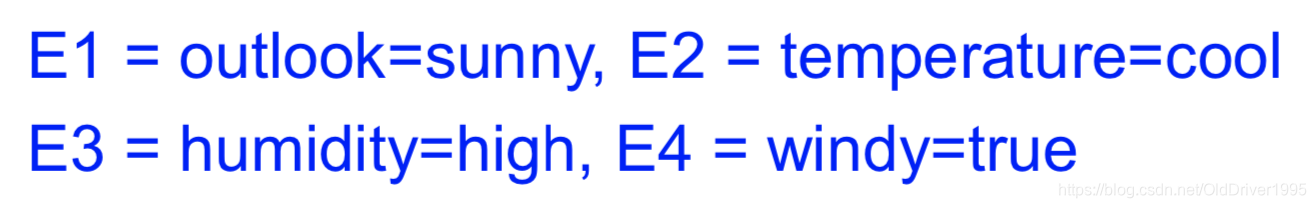
由于分母都是P(E) ，所以只需要比较分子的大小即可, 由于机器学习是基于过去数据对未来的预测，所以以上所有的概率都是从过去这几天的观测数据中获得，可以得知：

P(E1|yes) = (yes中outlook=sunny的次数) / 所有yes = 2/9

同理：

P(E2|yes) = 3/9 = 1/3

P(E3|yes) = 3/9 = 1/3

P(E4|yes) = 3/9 = 1/3

P(yes) = 9/14

P(E1|no) = 3/5

P(E2|no) = 1/5

P(E3|no) = 4/5

P(E4|no) = 3/5

P(no) = 5/14

经过计算可得P（yes|E）的分子部分为1/189=0.0053， 而P（no|E）的分子部分为18/875=0.0206, 很明显后者概率更大，应该归位no。如果遇到某一项的概率为0，则会导致分子永远为0，为了避免这种情况，使用smoothing平滑处理或者叫Laplace correction拉普拉斯平滑处理, 这里不细究.

b)数字数据:

以上是对文本型(catagorical)的数据进行贝叶斯归类，但如果是数字型(numerical)的数据，则需要用到其他辅助手段，比如默认数据的分布是按照高斯（正态）分布的，则有了我们的GaussianNB（高斯贝叶斯）。当然数据并不一定是按照正态分布的，应对这种情况则需要选择使用其他的概率密度函数比如Poisson柏松，Gamma，binomial二项式。

如果是正态分布，则通过观测数据计算出均值mean和方差standard deviation然后代入正态分布的概率密度函数即可获得该特征的概率值，然后代入贝叶斯公式计算.

三）基于sklearn的代码实现：

由于所有的概率计算是基于过去的数据，所以对过去的数据（train set）的划分则会对未来的预判（predict）产生影响, 数据划分的好坏将会影响机器学习模型的各项性能指标。

以下是代码：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import os
from scipy import signal
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
#for accuracy_score, classification_report and confusion_matrix
from sklearn import metrics
from sklearn.metrics import accuracy_score
# to make this notebook's output stable across runs
np.random.seed(42)# load the iris dataset
from sklearn.datasets import load_iris
iris = load_iris()

导入了必要的包并且获得所有数据后，将会划分数据：

X_train, X_test, y_train, y_test = train_test_split(
iris.data, iris.target, stratify=iris.target, random_state=42)

这个stratify的作用是按照该标签中的各类所占比例来划分，比如y中的三种结果，0 1 2分别表示iris这些数据集中一共有三种花，加了这个之后train_test_split函数就会根据这个比例来划分，使得train set和test set中尽量都是这个比例。

这个random_state也是让每次划分固定的，甚至换了其他电脑也会参照同样的方式划分，使得结果一致。而如果不加这个，划分将每次都不同。如果是其他值，则也是按另一种比例固定划分.

接下来就是引入GaussianNB模型并用train set数据让它学习：

from sklearn.naive_bayes import GaussianNB
clf=GaussianNB() 
clf.fit(X_train, y_train)

学习好之后利用测试集test set的数据来进行预测, 并且打印预测数据和真实的测试集数据进行对比:

y_predict = clf.predict(X_test)
print("predicted data:\n", y_predict)
print("actual data\n", y_test) #actual

可得结果如下，并且每次运行都是一样的结果，因为我们设置了random_state=42, 如果设置成其他值则会发生变化，这里不做过多测试:

可以发现大部分都预测的非常准确(准确率达92%），可以通过计算得知：

accuracy = ((y_predict-y_test)==0).sum()/len(y_test)

四） 性能分析perfomance evaluation：

当然，准确率并不是唯一评价ML模型好坏的标准，还有准确率precision，召回率recall，f1等指标。接下来将手动计算这几个值。在计算之前先要知道混淆矩阵confusion matrix：

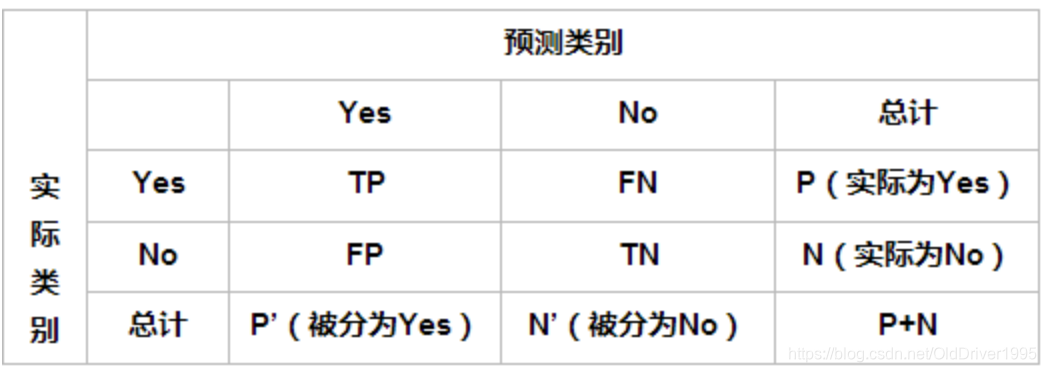
其中实际类别就是y_test, 而预测类别就是y_predict.

accuracy = (TP+TN)/all，即所有预测正确的/所有。

precision = TP/(TP+FP)

recall = TP/(TP+FN)

F1=2P*R /（P+R）

对于0这一类而言，TP = 12 , TN =26， FP = 0， FN = 0, 他们分别的意思是TP(y_test是0，y_predict也是0），TN（y_test不是0，y_predict也不是0，例如，1被预测成2，2被预测成1，1被预测成1，2被预测成2都属于这一类，只要不和0沾边的），FP(本来不是0，被预测成0,这里一个都没有）,FN（本来是0，被预测成不是0，这里一个没有）.

所以关于0的precision，recall，f1都为0

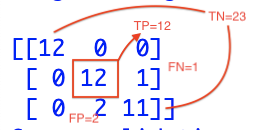
同理，对于1而言，TP=12, TN=23, FP=2, FN=1 (在上方测试结果中可以看到本来actual不是1，被预测成1的有2个，本应该actual是1的被预测成其他的，有1个）

所以accuracy=25/28=0.92, precision = 12/14=0.86, recall=12/13=0.92, f1=2* 0.86 *0.92/(0.86+0.92) = 0.889

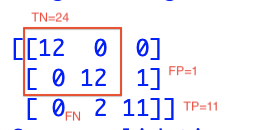
对于2，TP=11, TN=24, FP=1, FN=2

accuracy=35/38=0.92, precision = 11/12=0.92, recall = 11/13=0.85, f1=0.883

接下来调用函数进行验证：

print(metrics.classification_report(y_test, y_predict))
print(metrics.confusion_matrix(y_test, y_predict))

得到结果如下:

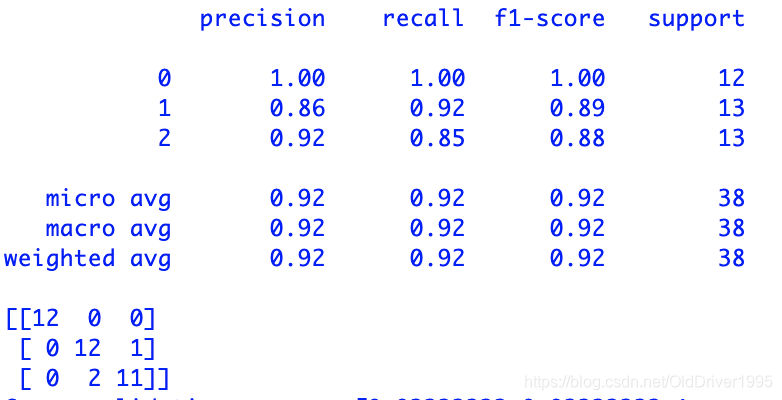
最后这个三维的混淆矩阵，左边栏是指实际值（test set），上方是指预测值（predict），由图可知，0全部划分正确，本身为1类，却被划分到2类的有1个（下图蓝框），本身为2类，却被划分到1类的有2个（下图红框）。

并且它虽然是三维的，但仍然能用来判断TP，TN，FP，FN

先看最简单的0:

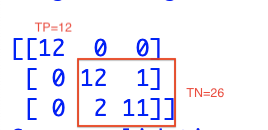
再是相对简单的2:

最后一丢丢复杂的1:

五）绘制决策边界Decision Boundary

代码如下：

from matplotlib.colors import ListedColormap
def plot_decision_boundary(clf ,axes):xp=np.linspace(axes[0], axes[1], 200)yp=np.linspace(axes[2], axes[3], 200)x1, y1=np.meshgrid(xp, yp)xy=np.c_[x1.ravel(), y1.ravel()]y_pred = clf.predict(xy).reshape(x1.shape)custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])plt.contourf(x1, y1, y_pred, alpha=0.3, cmap=custom_cmap)plot_decision_boundary(clf , axes=[4, 8, 1.5, 5])
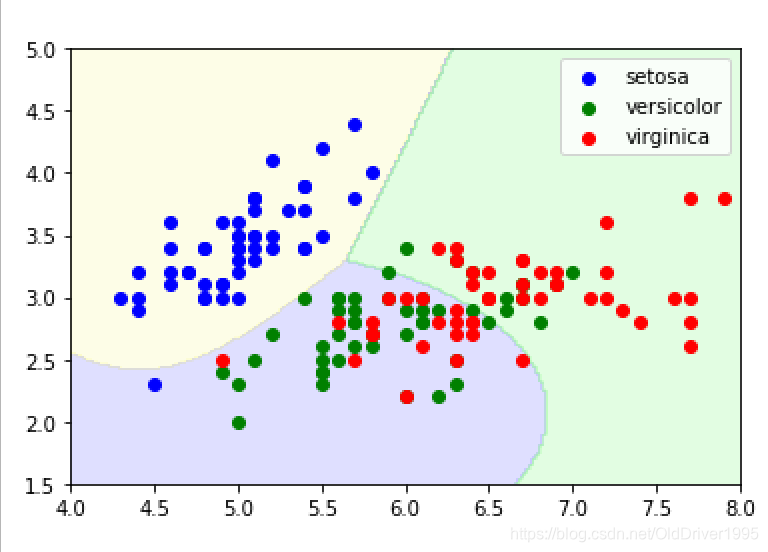
p1 = plt.scatter(X[y==0,0], X[y==0, 1], color='blue')
p2 = plt.scatter(X[y==1,0], X[y==1, 1], color='green')
p3 = plt.scatter(X[y==2,0], X[y==2, 1], color='red')
#设置注释
plt.legend([p1, p2, p3], iris['target_names'], loc='upper right')
plt.show()

绘制结果如图：

六）交叉验证cross validation

a)k-fold cv k折交叉验证

10折的交叉验证10-fold cross-validation, cv这个参数默认为3，这里改成10层:

from sklearn.model_selection import cross_val_score
scores = cross_val_score(clf, iris.data, iris.target, cv=10)

查看结果：

print("Cross-validation scores: {}".format(scores)) 
#accuracy for each fold
print("Average cross-validation score: {:.2f}".format(scores.mean()))
#average accuracy over all folds

b）leave-one-out cross validation(LOOCV) 留一验证

LOOCV的好处是他不受数据集划分的影响，缺点是计算量太大，因为他会把每一个数据都用来当一次预测集，所有n-1个数据都用来做训练集, 代码如下：

from sklearn.model_selection import LeaveOneOut
one_out = LeaveOneOut()
scores = cross_val_score(clf, iris.data, iris.target, cv=one_out)
print("Number of evaluations: ", len(scores))
print("Mean accuracy: {:.2f}".format(scores.mean()))

可得结果分别是len = 150和accuracy = 0.95