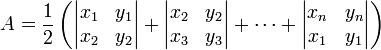林浩然积分大法征服曲边形面积

林浩然积分大法征服曲边形面积

Lin Haoran Masters Integral Arts to Conquer Curvilinear Area

在数学江湖中，林浩然这位智者不只精通“微分剑法”，还修炼了另一门绝技——“积分盾牌”。这一次，他用这门源于积分学的强大武学，幽默诙谐地破解了困扰众人已久的曲边形面积计算难题。

In the realm of mathematical adventures, Lin Haoran, the sage, not only excelled in the “Differential Sword Technique” but also cultivated another formidable skill—the “Integral Shield.” This time, he humorously unraveled the long-standing challenge of calculating the area of a curvilinear shape using this powerful martial art derived from integral calculus.

话说某日，国王面对一块形状奇特、边界曲折多变的土地犯了难：“如此复杂的曲边土地，究竟如何计算其精确的面积？”群臣束手无策之际，林浩然却轻松一笑，亮出了他的“积分盾牌”。

One day, faced with a piece of land with a peculiar shape and intricate boundaries, the king found himself in a quandary: “How can we precisely calculate the area of this complex curvilinear land?” With the courtiers at a loss, Lin Haoran smiled effortlessly, revealing his “Integral Shield.”

他生动比喻道：“你们看，这块曲边土地就像是一块由无数细小矩形拼接起来的大毯子。如果每一块小矩形都足够薄，那么它们叠加起来就能无限接近这片曲边土地的真实形状。而每个小矩形的面积我们都能够准确计算，通过累加所有这些小矩形的面积，我们便能以积分的形式求得这片复杂曲边土地的整体面积。”

He vividly explained, “Look, this curvilinear land is like a large quilt pieced together by countless tiny rectangles. If each small rectangle is thin enough, their superimposition can approximate the true shape of this curvilinear land. By accurately calculating the area of each small rectangle and summing up all these areas, we can obtain the overall area of this complex curvilinear land through the form of integration.”

接着，林浩然施展积分大法，将看似不可捉摸的曲边图形分割成无数个微小的矩形或梯形，通过分别计算每个小区域的面积，并累积相加，最终得到了那片神秘土地的精准面积。他的解题过程犹如一位巧匠细心编织，一片片碎片汇聚成一幅完整的画面，令人叹为观止。

Then, Lin Haoran wielded the power of integral arts, subdividing the seemingly elusive curvilinear shape into numerous tiny rectangles or trapezoids. By calculating the area of each small region separately and accumulating the results, he ultimately derived the precise area of that mysterious land. His problem-solving process resembled a meticulous craftsman weaving together fragments into a complete picture, leaving the audience in awe.

在笑声和掌声中，林浩然再次证明了积分思想的力量与魅力，他用风趣的语言和巧妙的比方，让枯燥的数学知识变得生动有趣，也使得原本棘手的问题迎刃而解。从此，林浩然的“积分盾牌”成为了人们解决复杂几何问题的一把金钥匙，传为佳话。

Amidst laughter and applause, Lin Haoran once again demonstrated the power and charm of integral thinking. With his witty language and clever analogies, he transformed the seemingly dull mathematical knowledge into a lively and engaging experience, effortlessly resolving the intricate problem. Henceforth, Lin Haoran’s “Integral Shield” became a celebrated tale, a golden key for people to solve complex geometric problems.

微积分的四大“乐高积木”

你知道吗？微积分就像一套数学界的乐高积木，只不过这些积木不是用来搭建城堡或飞船，而是用来构建我们对自然界复杂变化规律的理解。今天，我们要用轻松幽默的方式揭开这套神秘积木包——微积分四大核心理念的面纱。

第一块积木：极限（The Limit Brick）

想象一下你是个宇宙快递员，要把包裹送到无限小的一毫米处，每次尝试都更接近目标但永不真正到达。这就是极限的概念，它像是你在追求“哈利·波特”的隐形斗篷那样，虽然看不见摸不着，但你知道它就在那里，不断逼近。在数学的世界里，我们研究函数在某一点的行为，即使那个点像霍格沃茨一样隐藏在微观世界中。

第二块积木：导数（The Derivative Speedometer）

假设你在驾驶一辆名为“函数曲线号”的赛车，在赛道上疾驰。每当你瞬间换挡加速时，导数就是你的速度表，它告诉你那一刻赛车加速度的变化情况。换句话说，导数是函数在某一刻的瞬时变化率，就好比是你在决定超车前想知道的那一刹那间车子有多快，以便安全并优雅地完成超车动作。

第三块积木：积分（The Integral Area Counter）

如果你要装修一个奇形怪状的房间，而老板让你算出地毯需要多大面积，这时你就需要用到积分这个神奇的面积计算器了。积分就像是拥有魔法口袋的叮当猫，能将一条曲线上下任意切割成无数个小矩形（或者更好玩的是，可以是各种形状），然后把它们一一叠加起来，最终得到整个曲线下方的总面积。即使是月球表面那样的凹凸不平也能轻松应对，只要你有耐心和足够的积分技巧。

第四块积木：级数（The Series Juggler）

级数就像是数学马戏团中的杂技演员，他们不断地抛接一连串数字气球，每个气球代表一项，而当这些气球组合在一起且条件合适时，它们会聚合成一个有限的大数字或是无尽的循环表演。级数就是这样一种工具，通过求和无穷多个项来近似表示某个函数或者数值。就像观众眼花缭乱地看着杂技演员手中不停变换的气球序列，数学家们则是在计算和分析那些无穷级数以揭示其背后的秘密。

总结起来，微积分这四大核心理念就像一套趣味横生的数学积木，它们各自独立又紧密相连，共同搭建起我们理解世界的数学框架。只要我们掌握了这些积木的玩法，就能在解决实际问题时游刃有余，甚至还能玩转那些看似复杂的自然法则，是不是很酷呢？现在，让我们一起动手，开启这场从极限到级数的奇妙旅程吧！