本文主要是介绍Matlab|基于分布式ADMM算法的考虑碳排放交易的电力系统优化调度研究,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
1 主要内容
目标函数
计算步骤
节点系统
2 部分代码
3 程序结果
4 下载链接
1 主要内容
程序完全复现文献《A Distributed Dual Consensus ADMM Based on Partition for DC-DOPF with Carbon Emission Trading》,建立了一个考虑碳排放交易的最优模型,首先,对测试系统(6节点或者30节点或者118节点系统)进行了分区,以便后续ADMM算法的应用,其次,构建了DC-DOPF的最优潮流模型作为主要应用场景,以发电+买卖排放配额费用之和为目标函数,考虑碳排放约束、潮流约束以及耦合约束等约束条件,程序考虑了负荷需求响应和碳排放交易,从而符合目前低碳调度的研究热点,算法方面采用ADMM算法,也就是交替方向乘子法,更加创新,而且求解的效果更好,代码质量非常高,保姆级的注释以及人性化的模块子程序,所有数据均明确可靠来源,非常方便学习!

-
目标函数

-
计算步骤

-
节点系统
程序默认节点系统为118节点系统,代码如下:
FileName = 'SCUC_dat/DDOPF118.txt'; %Corresponding to the 118-bus system in literature [7];对应文献[7]中的118-bus system
可以通过修改节点系统名称来验证其他节点(6节点或者30节点)系统模型,程序已经内置了这部分代码,可以通过取消注释即可实现。
% FileName = 'SCUC_dat/SCUC6.txt'; %Corresponding to the 6-bus System;对应文中6bus例子 % FileName = 'SCUC_dat/SCUC30.txt'; %Corresponding to the 30-bus System;对应文中30bus例子 % FileName = 'SCUC_dat/SCUC6-2.txt'; %Corresponding to the 6-bus System in literature [7];对应文献[7]中的6-bus system % FileName = 'SCUC_dat/SCUC1062-2.txt'; %Corresponding to the 1062-bus System;对应文中1062-bus例子 % FileName = 'SCUC_dat/RTS48.txt'; %Corresponding to the RTS-48 bus system.The test system can obtain from [44];对应文中RTS0-48 bus例子
2 部分代码
if isequal(k,1) %第一次形成p_t并记下对应的区间即可p_t_index = []; %存储p_t中每行在XJ中的索引,第一列为初始索引,第二列为结束索引,第三列为行索引seta_t_index = []; %存储seta_t中每行在XJ中的索引,第一列为初始索引,第二列为结束索引,第三列为行索引for i = 1:size(allNodes,1)bus_sequence_index = find(ismember(SCUC_data.busUnits.bus_sequence,allNodes(i,1))==1); %allNodes(i,1)在SCUC_data.busUnits.bus_sequence上的索引P_start_index = (PbusUnitsNumber(i,1) - PbusUnitsNumber(1,1) + i - 1); %allNodes(i,1)对应变量P前面的所有变量P和θ的总数量Seta_start_index = (PbusUnitsNumber(i+1,1) - PbusUnitsNumber(1,1) + i - 1); %allNodes(i,1)对应变量θ前面的所有变量P和θ的总数量if ~isempty(bus_sequence_index) %The bus with unit. 节点上有发电机for j = 1:size(SCUC_data.busUnits.unitIndex{bus_sequence_index,1},1)p_t(units_number,:) = XJ(P_start_index*T + (j-1)*T + 1:P_start_index*T + (j-1)*T + T);%Pp_t_index(units_index,1) = P_start_index*T + (j-1)*T + 1;p_t_index(units_index,2) = P_start_index*T + (j-1)*T + T;p_t_index(units_index,3) = units_number;units_number = units_number + 1;units_index = units_index + 1;endelse %The bus without unit.节点上没有发电机p_t(units_number,:) = XJ(P_start_index*T + 1:P_start_index*T + T);%Punits_number = units_number + 1;endseta_t(i,:) = XJ(Seta_start_index*T + 1:Seta_start_index*T + T);%θseta_t_index(i,1) = Seta_start_index*T + 1;seta_t_index(i,2) = Seta_start_index*T + T;seta_t_index(i,3) = i;endelse %按照第一次记下的变量顺序即可p_t = zeros(partitionData.PIUnitsNumber{end}-partitionData.PIUnitsNumber{1},T);seta_t = zeros(size(seta_t_index,1),T);for i = 1:size(p_t_index,1)p_t(p_t_index(i,3),:) = XJ(p_t_index(i,1):p_t_index(i,2));endfor i = 1:size(seta_t_index,1)seta_t(seta_t_index(i,3),:) = XJ(seta_t_index(i,1):seta_t_index(i,2));endendelseif isequal(includeDR,'yes')PINumber = partitionData.PINumber;EINumber = partitionData.EINumber;piecewiseNumber = SCUC_data.elasticBus.piecewiseNumber; %分段函数分的段数K = SCUC_data.elasticBus.N;%弹性节点数量dr_t = zeros(K,T); %弹性负荷变量drhr_t = zeros(piecewiseNumber,T,K); %辅助变量Hr,第一个参数对应分段数,第二个参数对应时段,第三个参数对应节点编号%按照片区顺序for i = 1:nDindex = 2*(PINumber{i+1}-1)*T + (EINumber{i}-1)*(piecewiseNumber+1)*T; %+2为考虑碳排放的两个变量Hindex = Dindex + T; %取dr和hrfor j = 1:EINumber{i+1}-EINumber{i}%dr的行按照partitionData.allElasticityNodes中节点编号的顺序dr_t(EINumber{i}-1+j,:) = XJ((j-1)*(piecewiseNumber+1)*T+1+Dindex:(j-1)*(piecewiseNumber+1)*T+T+Dindex); %drfor r = 1:piecewiseNumberhr_t(r,:,EINumber{i}-1+j) = XJ((j-1)*(piecewiseNumber+1)*T+(r-1)*T+1+Hindex:(j-1)*(piecewiseNumber+1)*T+(r-1)*T+T+Hindex); %hrendendendif isequal(k,1) p_t_index = []; %存储p_t中每行在XJ中的索引,第一列为初始索引,第二列为结束索引,第三列为行索引seta_t_index = []; %存储seta_t中每行在XJ中的索引,第一列为初始索引,第二列为结束索引,第三列为行索引%按照片区顺序for i = 1:nPindex = 2*(PINumber{i}-1)*T + (EINumber{i}-1)*(piecewiseNumber+1)*T; %+2为考虑碳排放的两个变量Dindex = 2*(PINumber{i+1}-1)*T + (EINumber{i}-1)*(piecewiseNumber+1)*T; %+2为考虑碳排放的两个变量Hindex = Dindex + T; %取P和θfor j = 1:PINumber{i+1}-PINumber{i}%xx的行按照partitionData.allNodes(即allNodes)中节点编号的顺序p_t(PINumber{i}-1+j,:) = XJ(2*(j-1)*T+1+Pindex:2*(j-1)*T+T+Pindex);%Pseta_t(PINumber{i}-1+j,:) = XJ(2*(j-1)*T+T+1+Pindex:2*(j-1)*T+2*T+Pindex);%θp_t_index(PINumber{i}-1+j,1) = 2*(j-1)*T+1+Pindex;p_t_index(PINumber{i}-1+j,2) = 2*(j-1)*T+T+Pindex;p_t_index(PINumber{i}-1+j,3) = PINumber{i}-1+j;seta_t_index(PINumber{i}-1+j,1) = 2*(j-1)*T+T+1+Pindex;seta_t_index(PINumber{i}-1+j,2) = 2*(j-1)*T+2*T+Pindex;seta_t_index(PINumber{i}-1+j,3) = PINumber{i}-1+j;endendelse %按照第一次记下的变量顺序即可p_t = zeros(size(p_t_index,1),T);seta_t = zeros(size(seta_t_index,1),T);for i = 1:size(p_t_index,1)p_t(p_t_index(i,3),:) = XJ(p_t_index(i,1):p_t_index(i,2));endfor i = 1:size(seta_t_index,1)seta_t(seta_t_index(i,3),:) = XJ(seta_t_index(i,1):seta_t_index(i,2));endendelsedr_t = []; %弹性负荷变量drhr_t = []; %辅助变量Hrfor i = 1:Np_t(i,:) = XJ((i-1)*2*T+1:(i-1)*2*T+T);%Pseta_t(i,:) = XJ((i-1)*2*T+T+1:(i-1)*2*T+2*T);%θendend
3 程序结果

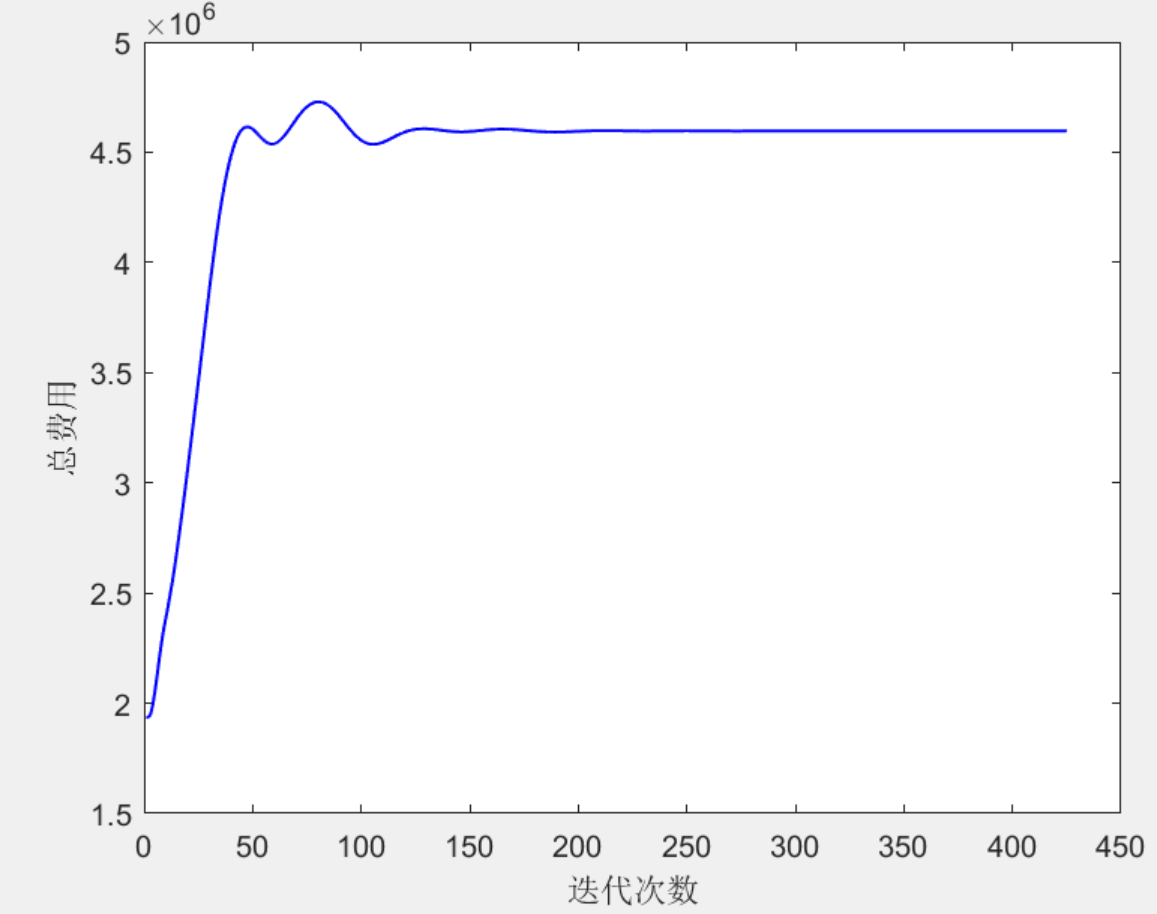
原文结果图:
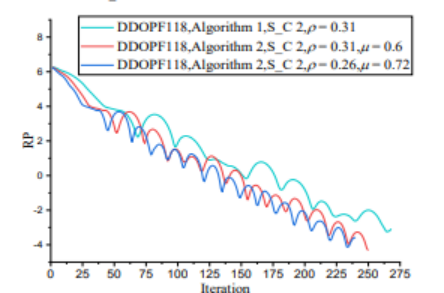
该图和上述结果图1趋势完全一致,验证代码的可行性。
4 下载链接
这篇关于Matlab|基于分布式ADMM算法的考虑碳排放交易的电力系统优化调度研究的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







