admm专题
理解ADMM, ALF和Split Bregman
理解ADMM, ALM和Split Bergman 引言Alternating Direction Method of MultipliersAugmented Lagrangian Multipliers小结Splitt Bregman 引言 在图像去模糊,低光照图像增强和去噪等任务时,我们都会引入各种先验或约束项来缓解这些t逆问题(inverse problems)的病态性
Matlab|基于分布式ADMM算法的考虑碳排放交易的电力系统优化调度研究
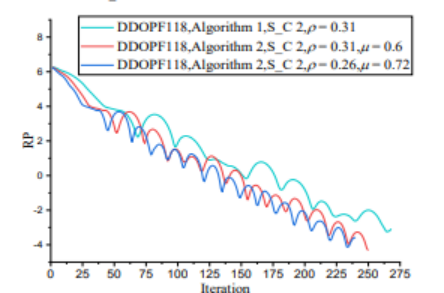
目录 1 主要内容 目标函数 计算步骤 节点系统 2 部分代码 3 程序结果 4 下载链接 1 主要内容 程序完全复现文献《A Distributed Dual Consensus ADMM Based on Partition for DC-DOPF with Carbon Emission Trading》,建立了一个考虑碳排放交易的最优模型,首先,对测试系统(6
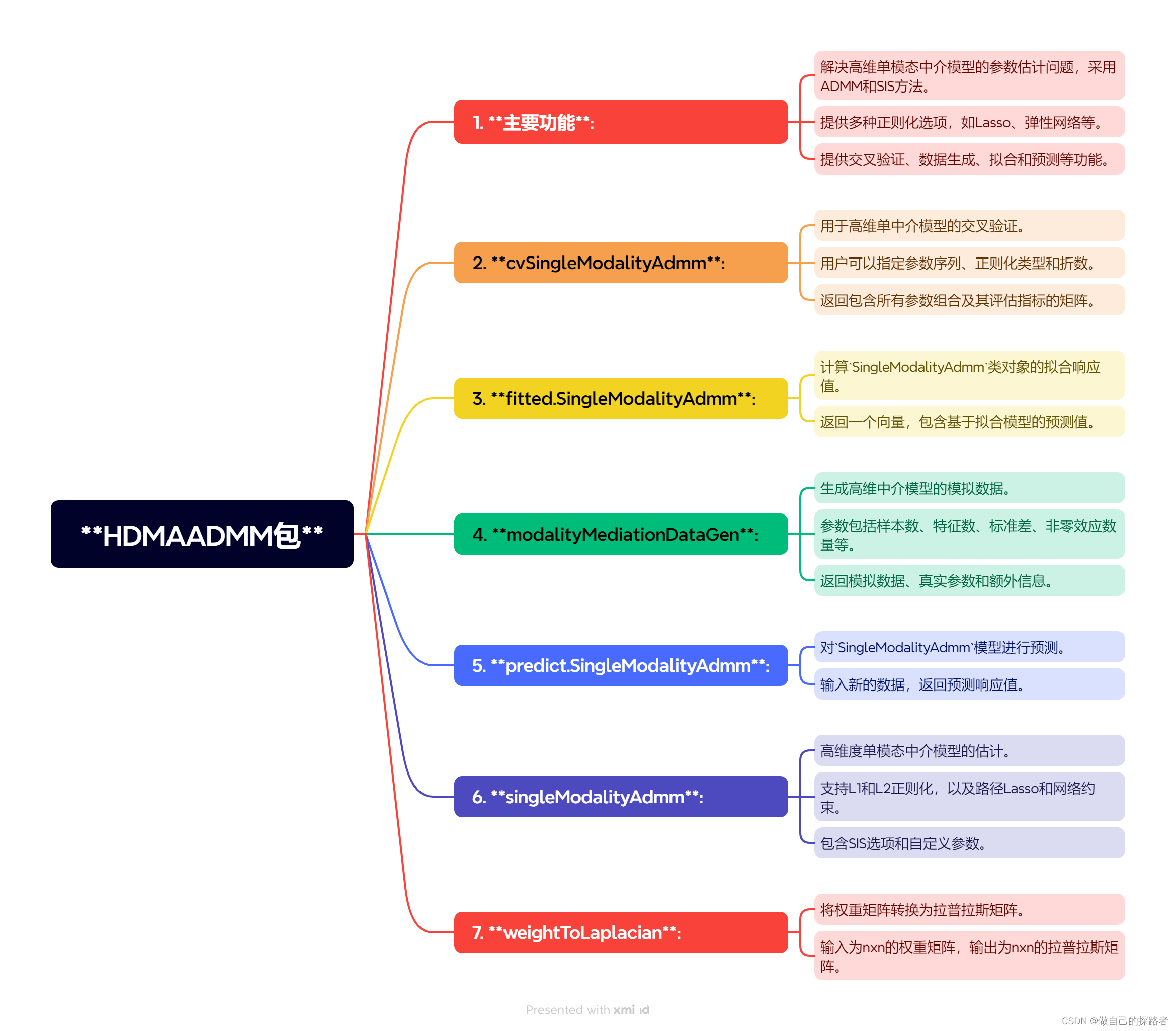
高维中介数据:基于交替方向乘子法(ADMM)的高维度单模态中介模型的参数估计(入门+实操)
全文摘要 用于高维度单模态中介模型的参数估计,采用交替方向乘子法(ADMM)进行计算。该包提供了确切独立筛选(SIS)功能来提高中介效应的敏感性和特异性,并支持Lasso、弹性网络、路径Lasso和网络约束惩罚等不同正则化方法。 Pathway Lasso 背景 传统的结构方程建模(SEM)在处理大量中介变量时变得不稳定且计算复杂。Pathway Lasso引入了一个新的惩罚函数,它是一
即插即用型ADMM应用于图像超分
Plug-and-Play优化公式 x ^ = arg min x f ( x ) + λ g ( x ) \hat{x}=\argmin_{x} f(x)+\lambda g(x) x^=xargminf(x)+λg(x) (1) 首先这是一个最大后验的问题,我们可以用ADMM方法转化为下面的算式: { x ( k + 1 ) = arg min x f ( x ) + ρ
从增广拉格朗日法到ADMM
从增广拉格朗日法到ADMM 增广拉格朗日法ADMM 增广拉格朗日法 考虑如下一个凸优化问题: 它的增广拉格朗日函数如下所示: 其中, λ λ λ是拉格朗日乘子,附加的二次项是线性约束 A x = b Ax = b Ax=b的惩罚项(penalty),增广拉格朗日法的第 k k k次迭代始于一个给定的 λ λ λk, 并通过如下式子得到 w w wk+1 =( x x xk+1
用于图像恢复的即插即用 ADMM:定点收敛和应用(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭:行百里者,半于九十。 📋📋📋本文目录如下:🎁🎁🎁 目录 💥1 概述 📚2 运行结果 2.1 算例1 2.2 算例2 🎉3 参考文献 🌈4 Matlab代码、数据、文献 💥1 概述 乘法交替方向法(ADMM)是