本文主要是介绍R语言逻辑回归与lasso模型,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、数据描述
数据集heart_learning.csv与heart_test.csv是关于心脏病的数据集,heart_learning.csv是训练数据集,heart_test.csv是测试数据集。
| 变量名称 | 变量说明 |
| age | 年龄 |
| sex | 性别,取值1代表男性,0代表女性 |
| pain | 胸痛的类型,取值1,2,3,4,代表4种类型 |
| bpress | 入院时的静息血压(单位:毫米汞柱 |
| chol | 血清胆固醇(单位:毫克/分升 |
| bsugar | 空腹血糖是否大于120毫克/公升,1代表是,0代表否 |
| ekg | 静息心电图结果,取值0,1,2代表3中不同的结果 |
| thalach | 达到的最大心率 |
| exang | 是否有运动性心绞痛,1代表是0代表否 |
| oldpeak | 运动引起的ST段压低 |
| slope | 锻炼高峰期ST段的斜率,取值1代表上斜,2代表平坦,3代表下斜 |
| ca | 荧光染色的大血管数目,取值为0,1,2,3 |
| thal | 取值3代表正常,取值6代表固定缺陷,取值7代表可逆缺陷 |
| target | 因变量,直径减少50%以上的大血管数目,取值0,1,2,3,4 |
| target2 | 因变量,取值1表示target大于0,取值0表示target等于0 |
二、读取数据集
heart_learning<-read.csv('f:/桌面/heart_learning.csv',colClasses = rep('numeric',15))
head(heart_learning)
heart_test<-read.csv('f:/桌面/heart_test.csv',colClasses = rep('numeric',15))
head(heart_test)
三、数据整理
将不是哑变量形式的定类自变量转换为因子变量,在本例中主要转换的变量为pain,ekg,slope,ca,thal,使用管道函数%>%和mutate()将两个数据集的变量进行类型转换。
heart_learning<-heart_learning %>% mutate(pain=as.factor(pain)) %>% mutate(ekg=as.factor(ekg)) %>%mutate(slope=as.factor(slope)) %>% mutate(thal=as.factor(thal))
heart_test<-heart_test %>% mutate(pain=as.factor(pain)) %>% mutate(ekg=as.factor(ekg)) %>% mutate(slope=as.factor(slope)) %>% mutate(thal=as.factor(thal))
转换后:
str(heart_learning) str(heart_test)
str(heart_learning) 'data.frame': 206 obs. of 15 variables:$ age : num 63 37 41 56 57 57 56 52 57 54 ...$ sex : num 1 1 0 1 0 1 0 1 1 1 ...$ pain : Factor w/ 4 levels "1","2","3","4": 1 3 2 2 4 4 2 3 3 4 ...$ bpress : num 145 130 130 120 120 140 140 172 150 140 ...$ chol : num 233 250 204 236 354 192 294 199 168 239 ...$ bsugar : num 1 0 0 0 0 0 0 1 0 0 ...$ ekg : Factor w/ 3 levels "0","1","2": 3 1 3 1 1 1 3 1 1 1 ...$ thalach: num 150 187 172 178 163 148 153 162 174 160 ...$ exang : num 0 0 0 0 1 0 0 0 0 0 ...$ oldpeak: num 2.3 3.5 1.4 0.8 0.6 0.4 1.3 0.5 1.6 1.2 ...$ slope : Factor w/ 3 levels "1","2","3": 3 3 1 1 1 2 2 1 1 1 ...$ ca : num 0 0 0 0 0 0 0 0 0 0 ...$ thal : Factor w/ 3 levels "3","6","7": 2 1 1 1 1 2 1 3 1 1 ...$ target : num 0 0 0 0 0 0 0 0 0 0 ...$ target2: num 0 0 0 0 0 0 0 0 0 0 ...
str(heart_test) 'data.frame': 91 obs. of 15 variables:$ age : num 44 43 59 44 61 59 44 65 51 45 ...$ sex : num 1 1 1 1 1 1 1 0 0 1 ...$ pain : num 2 4 4 3 3 3 2 3 3 4 ...$ bpress : num 120 150 135 130 150 150 130 155 140 104 ...$ chol : num 263 247 234 233 243 212 219 269 308 208 ...$ bsugar : num 0 0 0 0 1 1 0 0 0 0 ...$ ekg : num 0 0 0 0 0 0 2 0 2 2 ...$ thalach: num 173 171 161 179 137 157 188 148 142 148 ...$ exang : num 0 0 0 1 1 0 0 0 0 1 ...$ oldpeak: num 0 1.5 0.5 0.4 1 1.6 0 0.8 1.5 3 ...$ slope : num 1 1 2 1 2 1 1 1 1 2 ...$ ca : num 0 0 0 0 0 0 0 0 1 0 ...$ thal : num 7 3 7 3 3 3 3 3 3 3 ...$ target : num 0 0 0 0 0 0 0 0 0 0 ...$ target2: num 0 0 0 0 0 0 0 0 0 0 ...
四、二元逻辑回归
1、建立二元变量target2对自变量age,sex,pain,bpress,chol,bsugar,ekg,thalach,exang,等自变量的回归模型,因为因变量target2仅取0和1两值,因此该模型为普通的logistic逻辑模型。
fit_lm<-glm(target2~.,data=heart_learning[,-14],family = 'binomial')
summary(fit_lm)
summary(fit_lm)Call: glm(formula = target2 ~ ., family = "binomial", data = heart_learning[, -14])Coefficients:Estimate Std. Error z value Pr(>|z|) (Intercept) -6.079e+00 3.764e+00 -1.615 0.10634 age -2.382e-02 3.151e-02 -0.756 0.44975 sex 1.771e+00 6.958e-01 2.545 0.01091 * pain2 1.144e+00 9.911e-01 1.154 0.24837 pain3 5.378e-01 8.215e-01 0.655 0.51267 pain4 2.277e+00 8.550e-01 2.663 0.00774 ** bpress 4.034e-02 1.517e-02 2.658 0.00786 ** chol 8.330e-03 5.616e-03 1.483 0.13804 bsugar -6.162e-01 8.091e-01 -0.762 0.44631 ekg1 1.376e+01 1.587e+03 0.009 0.99309 ekg2 8.554e-01 5.142e-01 1.664 0.09619 . thalach -3.648e-02 1.502e-02 -2.428 0.01516 * exang 7.524e-01 5.533e-01 1.360 0.17385 oldpeak 6.505e-01 3.237e-01 2.010 0.04446 * slope2 4.972e-01 6.077e-01 0.818 0.41329 slope3 -4.059e-01 1.358e+00 -0.299 0.76504 ca 9.082e-01 3.277e-01 2.772 0.00558 ** thal6 9.011e-02 1.181e+00 0.076 0.93920 thal7 1.639e+00 5.651e-01 2.901 0.00372 ** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1(Dispersion parameter for binomial family taken to be 1)Null deviance: 284.00 on 205 degrees of freedom Residual deviance: 121.07 on 187 degrees of freedom AIC: 159.07Number of Fisher Scoring iterations: 15
运行得到了回归模型的系数。
2、将在训练数据集中得到的逻辑回归模型运用到测试数据,用以检验模型的拟合情况。
test.pred<-predict(fit_lm,heart_test,type = 'response')
head(test.pred)
type = 'response'表明拟合的类型为因变量target2取值为1的概率。
head(test.pred)1 2 3 4 5 6 0.13562868 0.44796749 0.63351630 0.04108158 0.29696382 0.06530277
test.pred.class<-1*(test.pred>0.5)
test.pred.class
表明当因变量target2预测的概率取值大于0.5是,该target2就取值为1,反之小于0.5时则取值为0.
运行得到预测的分类取值,
test.pred.class1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 0 0 1 1 0 1 0 0 0 0 0 1 1 0 1 1 0 1 1 1 0 0 0 1 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 79 80 81 82 83 84 85 86 87 88 89 90 91 1 1 1 1 1 1 1 1 1 1 1 1 1
table(heart_test$target2,test.pred.class)
则得到了真实的分类取值和预测值的列联表
table(heart_test$target2,test.pred.class)test.pred.class0 10 41 71 10 33
五、多值逻辑变量回归
1、即要求因变量taregt对自变量age,sex,pain,bpress等自变量进行回归分析,因变量target取值为0,1,2,3,4这5个取值。
library(MASS)
fit.ologit <- polr(as.factor(target) ~ ., data=heart_learning[,-15])
summary(fit.ologit)模型的系数
summary(fit.ologit)Re-fitting to get HessianCall: polr(formula = as.factor(target) ~ ., data = heart_learning[, -15])Coefficients:Value Std. Error t value age -0.014686 0.021748 -0.67527 sex 0.909686 0.432821 2.10176 pain2 0.618309 0.839876 0.73619 pain3 0.406543 0.729413 0.55736 pain4 1.668044 0.722760 2.30788 bpress 0.026835 0.010207 2.62913 chol 0.002481 0.003297 0.75255 bsugar -0.190277 0.495656 -0.38389 ekg1 1.303400 1.270044 1.02626 ekg2 0.658572 0.338254 1.94697 thalach -0.026755 0.009609 -2.78448 exang 0.312088 0.380035 0.82121 oldpeak 0.262455 0.176701 1.48530 slope2 0.596782 0.427343 1.39650 slope3 0.078796 0.860779 0.09154 ca 0.666761 0.201982 3.30109 thal6 1.030344 0.785958 1.31094 thal7 1.496852 0.404164 3.70357Intercepts:Value Std. Error t value 0|1 3.2295 2.4368 1.3253 1|2 5.0011 2.4493 2.0418 2|3 6.2313 2.4554 2.5378 3|4 8.1594 2.4755 3.2960Residual Deviance: 355.4983 AIC: 399.4983
2、将使用训练数据集中得到的模型运用到测试数据集,以验证模型的拟合预测情况
prob.ologit <- predict(fit.ologit, heart_test, type="probs")
head(prob.ologit)
head(prob.ologit)0 1 2 3 4 1 0.8329684 0.13405365 0.023110414 0.008420372 0.0014471768 2 0.6956545 0.23509494 0.047970289 0.018128313 0.0031519743 3 0.3538205 0.40919462 0.153773047 0.070184478 0.0130273377 4 0.9460872 0.04431458 0.006774099 0.002412405 0.0004116821 5 0.7037903 0.22941377 0.046307360 0.017455939 0.0030326152 6 0.9002005 0.08129427 0.013025629 0.004678986 0.0008006112
运行得到了因变量在每个样本观测中的取各种值的概率。
class.ologit <- predict(fit.ologit, heart_test, type="class")
class.ologit
运行得到了模型的预测分类取值情况。
class.ologit <- predict(fit.ologit, heart_test, type="class") > class.ologit[1] 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 0 0 1 0 0 0 0 0 3 1 0 1 1 0 [57] 1 3 3 0 0 0 1 0 0 1 3 3 3 3 1 3 0 0 3 1 1 3 1 3 1 4 1 3 3 1 4 3 1 1 3 Levels: 0 1 2 3 4
table(heart_test$target, class.ologit)
运行得到了测试数据的实际取值情况和模型预测的取值的列联表。
class.ologit0 1 2 3 40 44 3 0 1 01 9 5 0 3 02 2 3 0 6 03 0 5 0 4 24 0 2 0 2 0
六、将Lasso模型运用到二元逻辑模型。
此时模型的因变为target2,取1和0二值。
library(glmnet)
library(caret)
1、将分类变量转换为哑变量
dmy <- dummyVars(~pain+ekg+slope+thal,
heart_learning,
fullRank = TRUE)
2、将哑变量加进原始数据集中,并去除多余变量
heart_learning2 <- cbind(heart_learning,predict(dmy,heart_learning)) %>% dplyr::select(-c(pain,ekg,slope,thal)) %>% dplyr:: select(-c(target,target2),everything())
str(heart_learning2)
str(heart_learning2) 'data.frame': 206 obs. of 20 variables:$ age : num 63 37 41 56 57 57 56 52 57 54 ...$ sex : num 1 1 0 1 0 1 0 1 1 1 ...$ bpress : num 145 130 130 120 120 140 140 172 150 140 ...$ chol : num 233 250 204 236 354 192 294 199 168 239 ...$ bsugar : num 1 0 0 0 0 0 0 1 0 0 ...$ thalach: num 150 187 172 178 163 148 153 162 174 160 ...$ exang : num 0 0 0 0 1 0 0 0 0 0 ...$ oldpeak: num 2.3 3.5 1.4 0.8 0.6 0.4 1.3 0.5 1.6 1.2 ...$ ca : num 0 0 0 0 0 0 0 0 0 0 ...$ pain2 : num 0 0 1 1 0 0 1 0 0 0 ...$ pain3 : num 0 1 0 0 0 0 0 1 1 0 ...$ pain4 : num 0 0 0 0 1 1 0 0 0 1 ...$ ekg1 : num 0 0 0 0 0 0 0 0 0 0 ...$ ekg2 : num 1 0 1 0 0 0 1 0 0 0 ...$ slope2 : num 0 0 0 0 0 1 1 0 0 0 ...$ slope3 : num 1 1 0 0 0 0 0 0 0 0 ...$ thal6 : num 1 0 0 0 0 1 0 0 0 0 ...$ thal7 : num 0 0 0 0 0 0 0 1 0 0 ...$ target : num 0 0 0 0 0 0 0 0 0 0 ...$ target2: num 0 0 0 0 0 0 0 0 0 0 ...
3、建立lasso模型
fit.lasso <- glmnet(as.matrix(heart_learning2[,1:18]),
heart_learning2$target2,
family="binomial")
fit.lasso
Df %Dev Lambda 1 0 0.00 0.268700 2 2 3.89 0.244800 3 2 8.32 0.223100 4 3 12.46 0.203300 5 4 16.55 0.185200 6 4 20.23 0.168800 7 4 23.40 0.153800 8 6 26.51 0.140100 9 6 29.30 0.127700 10 6 31.75 0.116300 11 6 33.90 0.106000 12 6 35.79 0.096570 13 7 37.48 0.087990 14 7 39.01 0.080170 15 7 40.37 0.073050 16 8 41.58 0.066560 17 9 42.87 0.060650 18 9 44.22 0.055260 19 10 45.44 0.050350 20 10 46.60 0.045880 21 10 47.64 0.041800 22 10 48.56 0.038090 23 10 49.38 0.034710 24 11 50.15 0.031620 25 11 50.88 0.028810 26 11 51.53 0.026250 27 11 52.11 0.023920 28 11 52.62 0.021800 29 11 53.08 0.019860 30 12 53.50 0.018100 31 12 53.90 0.016490 32 12 54.26 0.015020 33 12 54.57 0.013690 34 12 54.84 0.012470 35 12 55.08 0.011360 36 12 55.29 0.010350 37 13 55.47 0.009435 38 15 55.67 0.008597 39 16 55.86 0.007833 40 16 56.05 0.007137 41 16 56.22 0.006503 42 16 56.36 0.005925 43 16 56.48 0.005399 44 16 56.58 0.004919 45 16 56.67 0.004482 46 16 56.75 0.004084 47 17 56.82 0.003721 48 17 56.90 0.003391 49 17 56.97 0.003090 50 17 57.03 0.002815 51 17 57.08 0.002565 52 17 57.13 0.002337 53 17 57.16 0.002130 54 18 57.19 0.001940 55 18 57.22 0.001768 56 18 57.24 0.001611 57 18 57.26 0.001468 58 18 57.28 0.001337 59 18 57.29 0.001219 60 18 57.30 0.001110 61 18 57.31 0.001012 62 18 57.32 0.000922 63 18 57.33 0.000840 64 18 57.33 0.000765 65 18 57.34 0.000697 66 18 57.34 0.000635 67 18 57.35 0.000579 68 18 57.35 0.000527 69 18 57.35 0.000481 70 18 57.36 0.000438 71 18 57.36 0.000399 72 18 57.36 0.000364 73 18 57.36 0.000331 74 18 57.36 0.000302 75 18 57.36 0.000275 76 18 57.36 0.000251
运行得到每次运行处理结果情况。

根据该模型,参数λ为调节参数,当λ逐渐增大是,所有模型系数都将趋于0,所有参数λ常用于变量选择。从图形中可以看到随着对数的λ值逐渐增大,每个变量代表的系数也逐渐趋于0.
3、使用交叉验证选取调节参数λ的值得到模型的回归系数
cvfit.lasso <- cv.glmnet(as.matrix(heart_learning2[,1:18]),
heart_learning2$target2,
family="binomial",
type.measure="class")
在这里使用了 cv.glmnet()函数,使用交叉验证选取调节参数的最佳值,因变量为二项分布,交叉验证的准则为错误分类率。
cvfit.lasso$lambda.min
运行得到了交叉验证的λ值为lmbda.min
cvfit.lasso$lambda.min [1] 0.02881333
coef(cvfit.lasso,s='lambda.min')
运行得到了模型的系数:
coef(cvfit.lasso,s='lambda.min') 19 x 1 sparse Matrix of class "dgCMatrix"s1 (Intercept) -1.6734148389 age . sex 0.5478601756 bpress 0.0123146239 chol 0.0005767132 bsugar . thalach -0.0184055035 exang 0.5116235150 oldpeak 0.3216762530 ca 0.4622937819 pain2 . pain3 . pain4 1.0975807443 ekg1 . ekg2 0.2317211271 slope2 0.2993419586 slope3 . thal6 . thal7 1.2936765301
上述系数中,没有显示系数值的变量将被剔除。
plot(cvfit.lasso)
运行得到: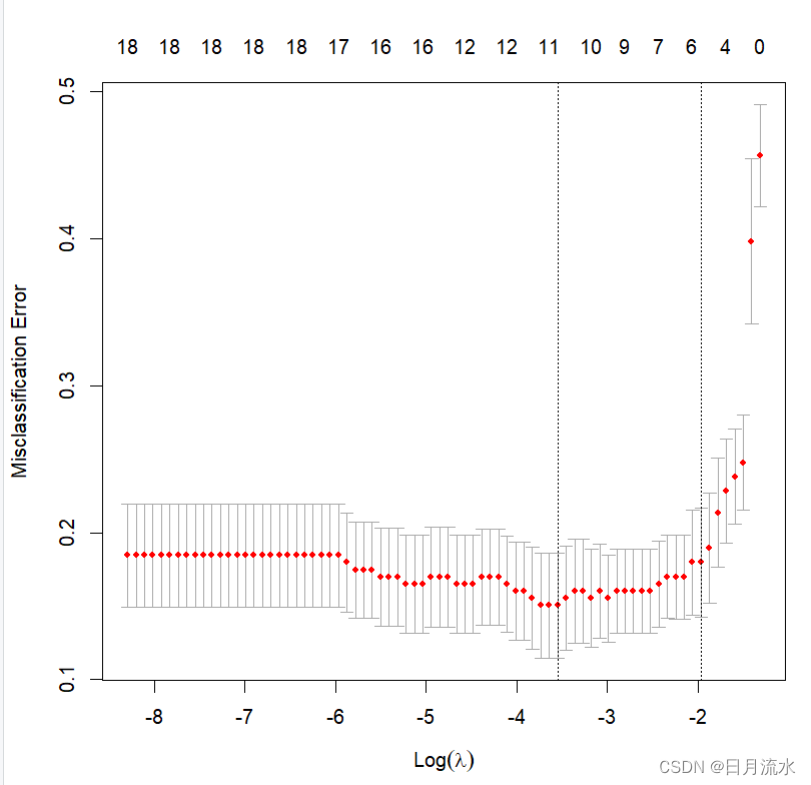
交叉验证的平均误差随着调节参数lambd对数值的变化而变化的图形,从图形中交叉验证的平均误差最小值对于的lambda,对数为-3.546917,相应的lambda的值为 0.02881333。从图形中最上面的对应数值看到,相应的选择进入模型变量为11个。
4、测试数据的拟合验证
heart_test2 <-
cbind(heart_test,predict(dmy,heart_test)) %>% dplyr::select(-c(pain,ekg,slope,thal)) %>%
dplyr::select(-c(target,target2),everything())
prob.lasso <-
predict(cvfit.lasso, as.matrix(heart_test2[,1:18]),
s="lambda.min", type="response")
对测试数据集进行整理,在整理后数据集进行进行lasso模型的拟合,得到因变量的概率取值的预测。
head(prob.lasso)lambda.min 1 0.1999511 2 0.3311122 3 0.6364576 4 0.1146022 5 0.3711861 6 0.1778357
class.lasso <-
predict(cvfit.lasso, as.matrix(heart_test2[,1:18]),
s="lambda.min", type="class")
head(class.lasso)
运行得到了因变量的取值情况
head(class.lasso)lambda.min 1 "0" 2 "0" 3 "1" 4 "0" 5 "0" 6 "0
table(heart_test$target2, class.lasso)
运行得到了因变量真实值和预测值的列联表。
table(heart_test$target2, class.lasso)class.lasso0 10 43 51 10 33
七、将Lasso模型运用到多值逻辑模型
相应的程序为:
cvfit2.lasso <- cv.glmnet(as.matrix(heart_learning2[,1:18]),
heart_learning2$target,
family="multinomial",
type.measure="class")
prob2.lasso <- predict(cvfit2.lasso, as.matrix(heart_test2[,1:18]),
s="lambda.min", type="response")
head(prob2.lasso)
得到:
head(prob2.lasso) , , 10 1 2 3 4 1 0.7819545 0.12867778 0.03665610 0.03401131 0.01870034 2 0.6889450 0.14948312 0.08312511 0.05084087 0.02760589 3 0.3670365 0.32374751 0.15268963 0.10556503 0.05096128 4 0.8866576 0.06487749 0.01947599 0.01893834 0.01005056 5 0.6836868 0.13274797 0.06431920 0.08618101 0.03306503 6 0.8531171 0.06231089 0.03283587 0.03465448 0.01708167得到因变量取值的概率
class2.lasso <- predict(cvfit2.lasso, as.matrix(heart_test2[,1:18]),
s="lambda.min", type="class")
得到了因变的预测值
head(class2.lasso)1 [1,] "0" [2,] "0" [3,] "0" [4,] "0" [5,] "0" [6,] "0"
table(heart_test2$target, class2.lasso)
因变量真实值和预测值列联表:
table(heart_test2$target, class2.lasso)class2.lasso0 1 2 30 45 2 1 01 12 3 2 02 2 5 2 23 2 6 1 24 1 1 1 1
本文结束。
这篇关于R语言逻辑回归与lasso模型的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




