本文主要是介绍清华大学《信号与系统》电力系统同步相量计算【FFT/谐波/小波变换】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
主要内容
该程序为清华大学《信号与系统》课程大作业的内容,内容研究深度和编程实现效果均较好,有详细的报告,是很好的参考资料,建议采用matlab高版本运行!
1.内容要求


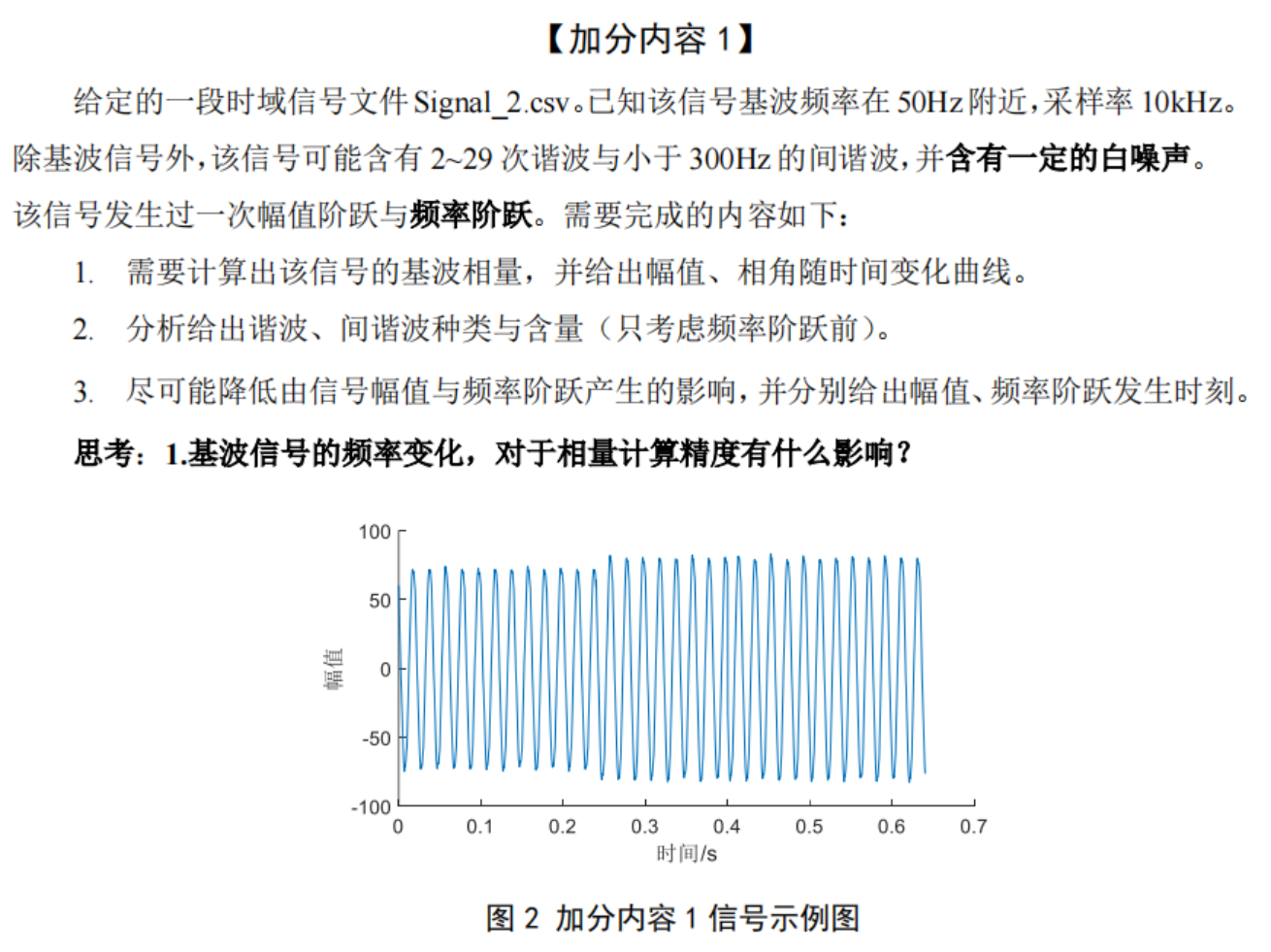
(还有加分内容2和3,篇幅原因不再展示)
2.研究方法
同步相量是以标准时间信号作为采样过程的基准,通过对采样数据计算而得到的相量,同步相量测量信息包含每个测量量值的幅值和相角以及相应的时间标签。数据采集与监视控制系统(Supervisory Control And Data Acquisition,SCADA)是以计算机为基础的电力自动化监控系统,其运用领域涵盖了电力、冶金、石油、化工等,SCADA在过去的电力系统监视中应用最为广泛,技术发展最为成熟。
新一代电网通过以同步相量测量技术为基础的广域测量系统来检测和控制系统的状态。同步相量测量技术的核心是相量估计算法的设计,即算法的估计精度将直接影响到的应用效果。本次大作业旨在运用信号与系统课程所学知识,对所给电压信号进行频谱分析,并设计算法计算信号的同步向量,主要包含两个部分:幅值计算、相位计算。
需要指出的是,同步向量的幅值为有效值,相位为余弦函数表示下的相位。
2.1 快速傅里叶变换FFT


2.2 窗函数法
在分析信号基波及各次谐波时,由于采样不满足完整周期,会造成泄露误差。处理泄露误差的一种有效方法是为信号加窗。FFT本质上是DFS,对于采样得到的一段有限长离散信号,使用FFT计算得到的结果实际上是将这一段离散信号周期延拓后的周期离散信号的DFS的结果(实际上是主值区间)。当采样不满足完整周期时,将信号周期延拓时显然可能会在拼接处出现间断点,这些间断点将会在频谱中产生本不存在的频率分量,造成泄露误差。
加窗分析的思路是非常直观的,原本一段有限长的离散信号相当于一个矩形窗作用在原始信号上,在信号边缘处没有衰减,如果现在使用一个边缘衰减的窗口,则在这段信号的两端的采样点的幅值都将趋于0,此时再进行拼接,原本的间断点就会被大大削弱,它们在频谱中产生的额外频率分量就会变得很小,所以泄露误差会得到限制。
2.3 希尔伯特-黄变换
希尔伯特-黄变换用于对一个信号进行平稳化处理,分析信号的幅值、频率阶跃。它包括经验模态分解( Empirical Mode Decomposition,EMD)和Hilbert 谱分析( Hilbert Spectrum Analysis,HSA)两部分。首先将时间信号通过经验模态分解 (EMD),产生一系列具有不同特征尺度的数据序列,每个序列称为一个固有模态函数(IMF),再分别针对每个固有模态函数进行HHT变换,得到各自频率和幅值的瞬时值。由此构建信号的时间-频率-能量三位分布图,即Hilbert谱,无论在时间域还是频率域都具有良好的分辨率,并且能更好地反映出信号的本质特征。其变换框图如图所示。

2.4 小波变换
小波变换能够对信号进行多分频率的频域分析。本次作业中主要利用小波变换去除信号中的白噪声。小波变换去噪方式有多种,本文选取的是非线性小波变换阈值法去噪。
部分代码
%双谱线插值初始版,用于求必做基波及谐波的平均频率、幅值、相位
clc;clear;close all;
wave = csvread('1_1.csv'); %load 数据
s=wave(1:3500,2);%由于在4800点前后会有幅值、频率阶跃,故不能直接对全部信号进行FFT,先截取前4500个点分析
fs=10000; %采样率
N=length(s);%采样点数
n=0:N-1;
M = 23;
w=0.5-0.5*cos(2*pi*(n)/N);%汉宁窗
r=s.*w';%对原信号加窗,信号乘以窗函数
v=fft(r,N);%进行FFT,返回N点的DFT
fuzhi=abs(v)/N*2*2;%求幅值并修正,修正系数为2
u=abs(v);
stem(fuzhi);%绘制出FFT后离散信号的茎状图,用于判断k0、k1、k2
A=zeros(1,30);%存储幅值
F=zeros(1,30);%存储频率
P=zeros(1,30);%存储相位
cishu=zeros(1,30);%存储次数
%以下为双峰谱线插值修正算法
for ii=0:29 %I+1对应谐波系数,题目说明只含有小于30次的谐波,故在29截止即可if(u(M - 1 + (M-1)*(ii)) > u(M + 1 + (M-1)*(ii)))k1 = M - 1 + (M-1)*(ii);k2 = M + (M-1)*(ii);else k1 = M + (M-1)*(ii);k2 = M + 1 + (M-1)*(ii);endy1 = u(k1);y2 = u(k2);b=(y2-y1)/(y2+y1);%相当于参考文献中的参数βa=1.5*b;%相当于参考文献中的参数αk0=k1+a+0.5-1;%峰值频率A(ii+1)=(y1+y2)*(2.35619403+1.15543628*a^2+0.32607873*a^4+0.07891461*a^6)/N;%修正后的幅值F(ii+1)=k0*fs/N; %频率不需要修正,P(ii+1)=(angle(v(M+1+6*ii))+pi/2-pi*(a-(-1)*0.5))/pi*180;
end
部分结果一览
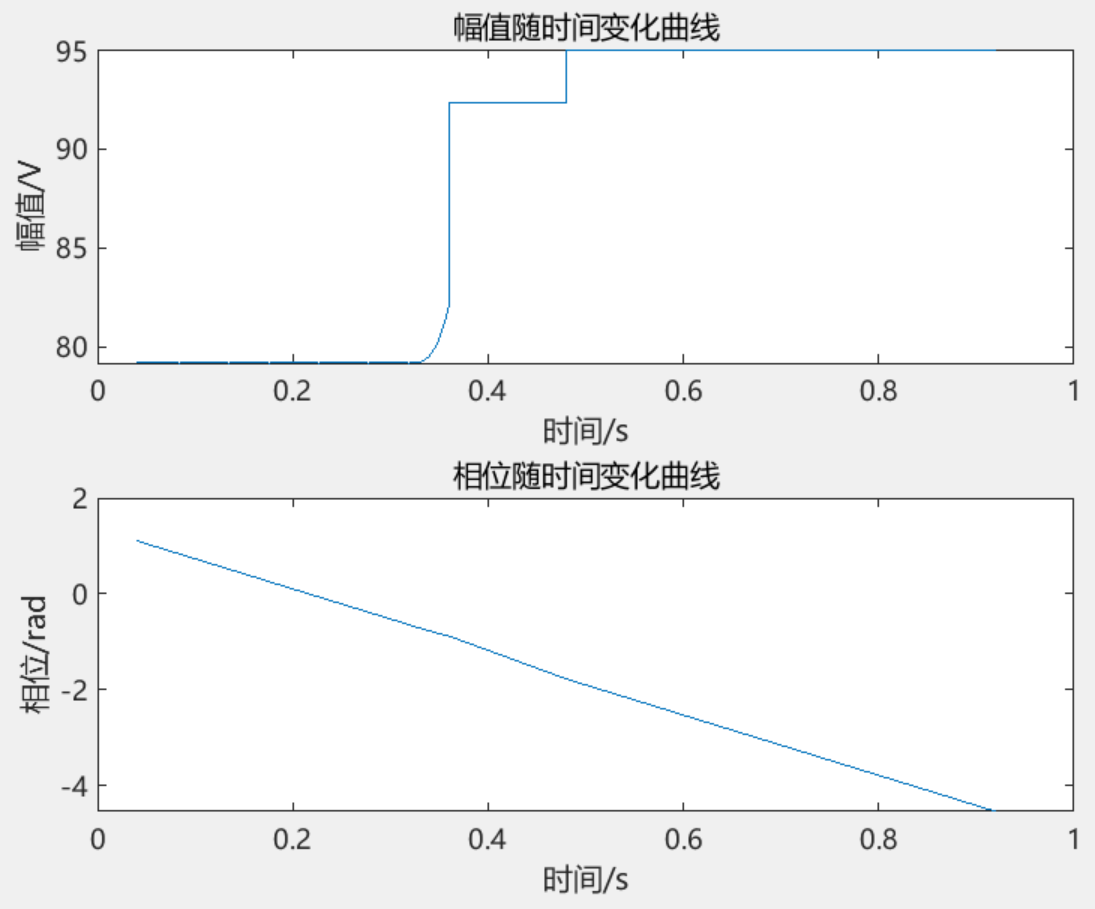
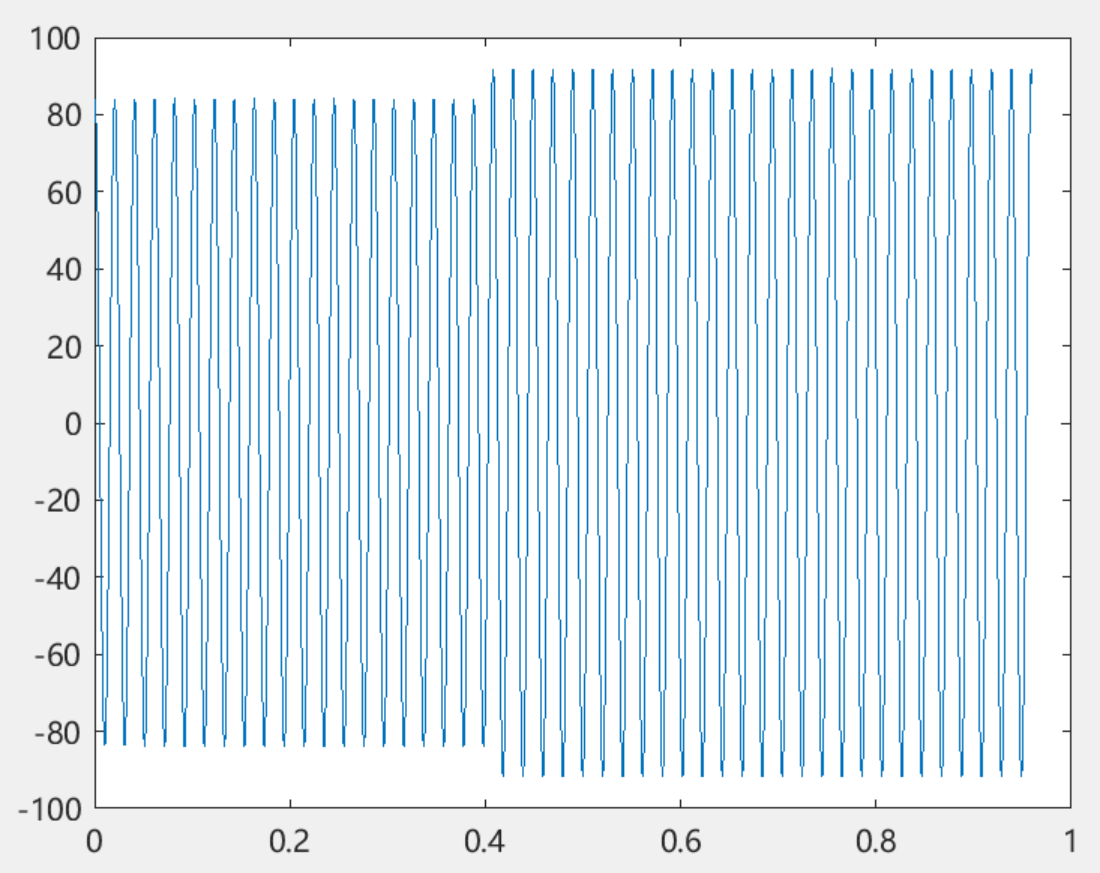
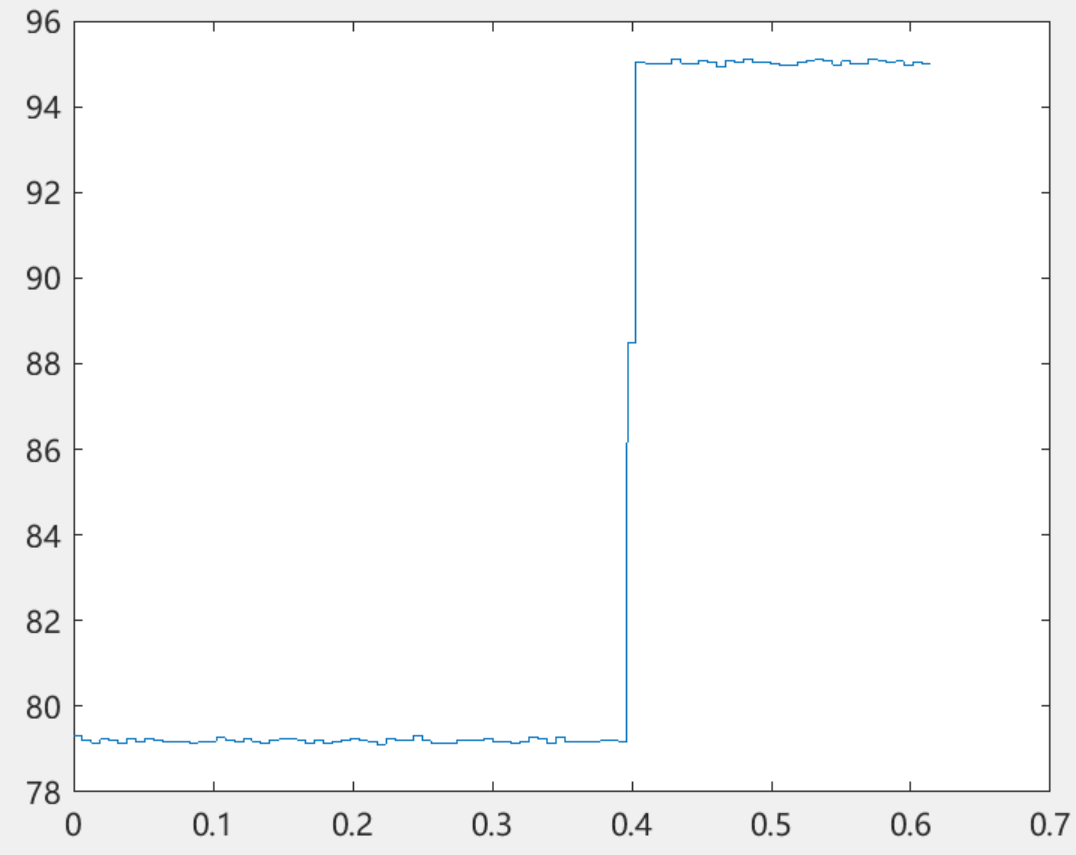
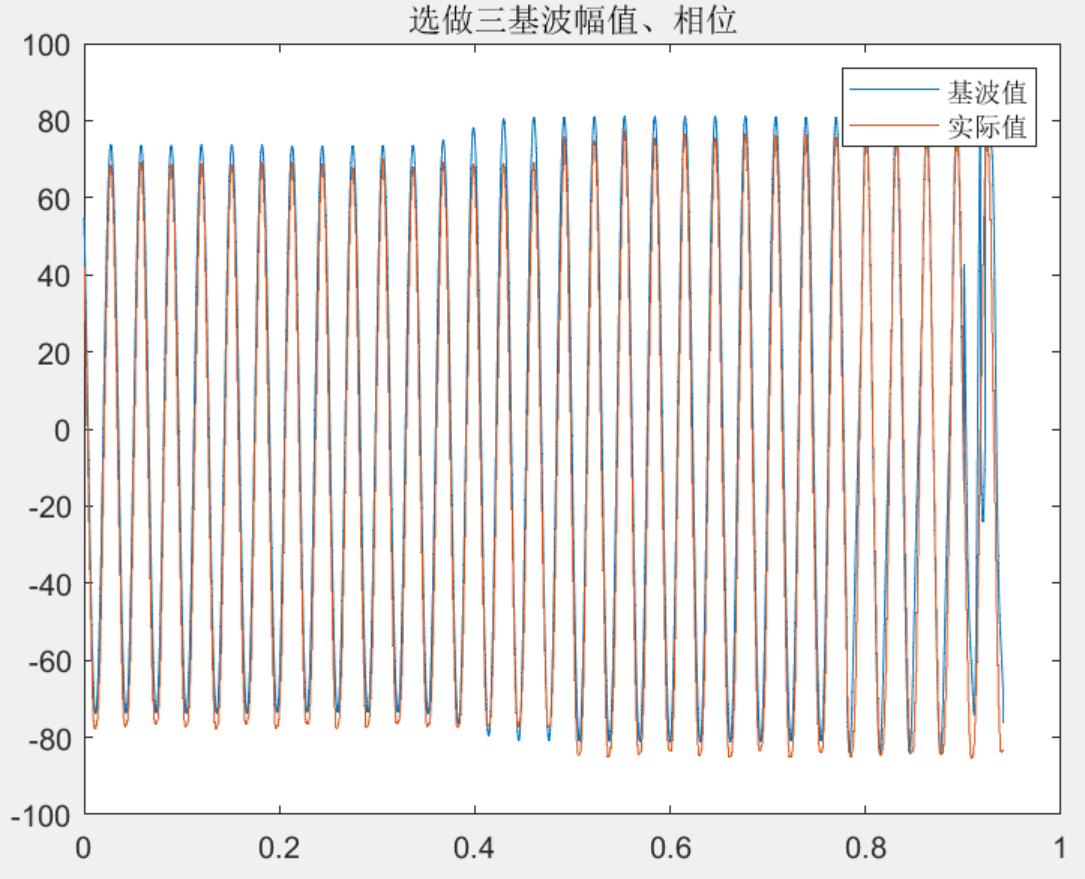

下载链接
这篇关于清华大学《信号与系统》电力系统同步相量计算【FFT/谐波/小波变换】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






