本文主要是介绍2023-03-26:给定一个二维数组matrix, 每个格子都是正数,每个格子都和上、下、左、右相邻。 你可以从任何一个格子出发,走向相邻的格子, 把沿途的数字乘起来,希望得到的最终数字中,结尾的0,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
2023-03-26:给定一个二维数组matrix,
每个格子都是正数,每个格子都和上、下、左、右相邻。
你可以从任何一个格子出发,走向相邻的格子,
把沿途的数字乘起来,希望得到的最终数字中,结尾的0最多,
走的过程中,向左走或者向右走的拐点,最多只能有一次。
返回结尾最多的0,能是多少。
1 <= 行、列 <= 400。
答案2023-03-26:
解题思路
本题需要求出从任意位置出发,最多能有多少个结尾0。为了方便计算,可以先将矩阵中每个数分解成2和5的因子,然后通过前缀和预处理出每个位置上、左方向的2和5的因子数量之和,以便快速计算6个方向上的因子数量之和。接着遍历每个位置,分别计算6个方向上的因子数量之和,并取其中的最小值,最后返回所有最小值中的最大值即可。
具体来说,对于一个位置(i,j),可以计算它的左、右、上、下4个方向的2和5的因子数量之和,以及两个斜方向的2和5的因子数量之和共6个值。然后取这6个值中的最小值,就是从该位置出发,在该方向上能够得到的最多结尾0的数量。遍历所有位置,取最大值即可。
需要注意的是,由于只能有一次向左或向右的拐点,因此在计算左和右方向上的因子数量之和时,需要分别计算到该行左边界和右边界的因子数量之和,然后再通过减法计算出中间部分的因子数量之和。
时间复杂度
本算法需要对矩阵中每个数进行分解质因数,时间复杂度为O(n ^ 2log(max(matrix)));两层循环分别对n和m进行遍历,时间复杂度为O(nm);因此总时间复杂度为O(n^2log(max(matrix))+nm)。
空间复杂度
本算法需要维护4个二维数组,每个数组的大小均为n×m,因此空间复杂度为O(nm)。
rust代码
fn most_trailing_zeros(matrix: &Vec<Vec<i32>>) -> i32 {let n = matrix.len(); // 矩阵行数let m = matrix[0].len(); // 矩阵列数// f2[i][j] : matrix[i][j]自己有几个2的因子let mut f2 = vec![vec![0; m]; n];// f5[i][j] : matrix[i][j]自己有几个5的因子let mut f5 = vec![vec![0; m]; n];// 预处理每个位置的2和5的因子数量for i in 0..n {for j in 0..m {f2[i][j] = factors(matrix[i][j], 2);f5[i][j] = factors(matrix[i][j], 5);}}// 计算每个位置上、左方向的2和5的因子数量之和let mut left_f2 = vec![vec![0; m]; n];let mut left_f5 = vec![vec![0; m]; n];let mut up_f2 = vec![vec![0; m]; n];let mut up_f5 = vec![vec![0; m]; n];for i in 0..n {for j in 0..m {left_f2[i][j] = f2[i][j] + if j > 0 { left_f2[i][j - 1] } else { 0 };left_f5[i][j] = f5[i][j] + if j > 0 { left_f5[i][j - 1] } else { 0 };up_f2[i][j] = f2[i][j] + if i > 0 { up_f2[i - 1][j] } else { 0 };up_f5[i][j] = f5[i][j] + if i > 0 { up_f5[i - 1][j] } else { 0 };}}let mut ans = 0;for i in 0..n {for j in 0..m {// 来到(i,j),计算6个方向上的因子数量之和let l2 = if j == 0 { 0 } else { left_f2[i][j - 1] }; // 左边的2因子数量之和 let l5 = if j == 0 { 0 } else { left_f5[i][j - 1] }; // 左边的5因子数量之和let r2 = left_f2[i][m - 1] - left_f2[i][j]; // 右边的2因子数量之和let r5 = left_f5[i][m - 1] - left_f5[i][j]; // 右边的5因子数量之和let u2 = if i == 0 { 0 } else { up_f2[i - 1][j] }; // 上面的2因子数量之和let u5 = if i == 0 { 0 } else { up_f5[i - 1][j] }; // 上面的5因子数量之和let d2 = up_f2[n - 1][j] - up_f2[i][j]; // 下面的2因子数量之和let d5 = up_f5[n - 1][j] - up_f5[i][j]; // 下面的5因子数量之和// 计算6个方向上因子数量之和最小的值let p1 = std::cmp::min(l2 + u2 + f2[i][j], l5 + u5 + f5[i][j]);let p2 = std::cmp::min(l2 + r2 + f2[i][j], l5 + r5 + f5[i][j]);let p3 = std::cmp::min(l2 + d2 + f2[i][j], l5 + d5 + f5[i][j]);let p4 = std::cmp::min(u2 + r2 + f2[i][j], u5 + r5 + f5[i][j]);let p5 = std::cmp::min(u2 + d2 + f2[i][j], u5 + d5 + f5[i][j]);let p6 = std::cmp::min(r2 + d2 + f2[i][j], r5 + d5 + f5[i][j]);// 取6个方向上的最小值中的最大值作为答案ans = std::cmp::max(ans,std::cmp::max(std::cmp::max(p1, p2),std::cmp::max(std::cmp::max(p3, p4), std::cmp::max(p5, p6)),),);}}ans
}// 计算num有几个f的因子
fn factors(num: i32, f: i32) -> i32 {let mut ans = 0;let mut num = num;while num % f == 0 {ans += 1;num /= f;}ans
}fn main() {let matrix1 = vec![vec![5, 8, 3, 1],vec![4, 15, 12, 1],vec![6, 7, 10, 1],vec![9, 1, 2, 1],];println!("{}", most_trailing_zeros(&matrix1)); // 输出:2let matrix2 = vec![vec![7500, 10, 11, 12],vec![6250, 13, 14, 15],vec![134, 17, 16, 1],vec![5500, 2093, 5120, 238],];println!("{}", most_trailing_zeros(&matrix2)); // 输出:13
}
运行结果
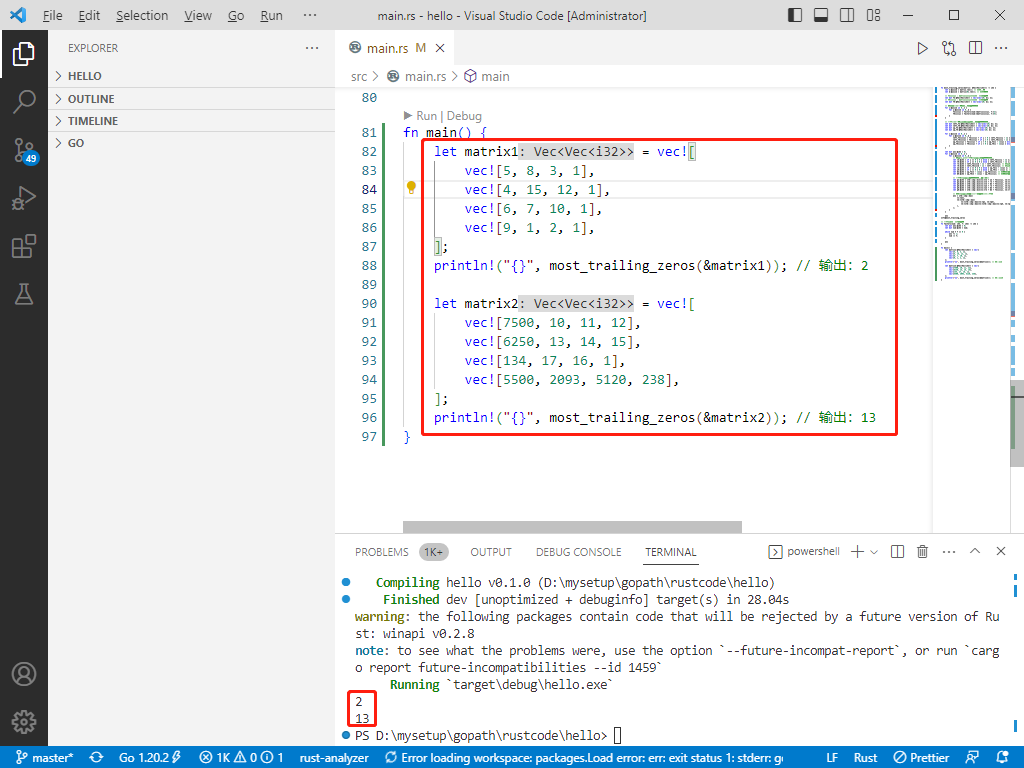
这篇关于2023-03-26:给定一个二维数组matrix, 每个格子都是正数,每个格子都和上、下、左、右相邻。 你可以从任何一个格子出发,走向相邻的格子, 把沿途的数字乘起来,希望得到的最终数字中,结尾的0的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






