本文主要是介绍tinyrenderer-Bresenham绘制直线算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
如何画线段
第一种尝试
求x,y起始点的差值,按平均间隔插入固定点数
起始点平均插入100个点:
void line(int x0, int y0, int x1, int y1, TGAImage& image, TGAColor color) {for (float t = 0.; t < 1.; t += .01) {int x = x0 + (x1 - x0) * t;int y = y0 + (y1 - y0) * t;image.set(x, y, color);}
}
//...
line(2, 52, 90, 80, image, white);
//...

问题:
线段距离过长,插入固定点数过少时,线段无法连续
插入10个点:
for (float t = 0.; t < 1.; t += .1) {

第二种尝试
根据 x轴的移动像素比例,给y轴线性插值
注意x轴的移动比例要转成float
void line(int x0, int y0, int x1, int y1, TGAImage &image, TGAColor color) { for (int x=x0; x<=x1; x++) { float t = (x-x0)/(float)(x1-x0); int y = y0*(1.-t) + y1*t; image.set(x, y, color); }
}
//...
line(13, 20, 80, 40, image, white);
line(20, 13, 40, 80, image, red);
line(80, 40, 13, 20, image, red);
//...

问题 :
- 当y轴移动距离大于x轴移动距离时,y轴的插入值会非常离散,因为y轴的插入频率小于x轴
- 起点x必须小于终点x
第三种尝试
判断线段的宽高比(斜率),以长的方向递增做为插值频率
并且对比起点,终点在递增方向轴的大小,以小的点做为递增起始点
void line(int x0, int y0, int x1, int y1, TGAImage &image, TGAColor color) { bool steep = false; if (std::abs(x0-x1)<std::abs(y0-y1)) { // if the line is steep, we transpose the image std::swap(x0, y0); std::swap(x1, y1); steep = true; } if (x0>x1) { // make it left−to−right std::swap(x0, x1); std::swap(y0, y1); } for (int x=x0; x<=x1; x++) { float t = (x-x0)/(float)(x1-x0); int y = y0*(1.-t) + y1*t; if (steep) { image.set(y, x, color); // if transposed, de−transpose } else { image.set(x, y, color); } }
}
//...
line(13, 20, 80, 40, image, white);
line(20, 13, 40, 80, image, red);
line(80, 40, 13, 20, image, red);
//...

问题:
效率低,做了多次除法和浮点数运算。10%的时间花在复制颜色上。但是70%的时间都花在了调用line()上
没有断言,没有越界检查等(这些文章里为了可读性,所以不处理)
第四种尝试
每个除法都有相同的除数,可以提到循环外
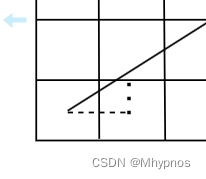
我们是以长轴每次递增1做为循环,因此另一个轴每次递增的插值是在[0,1]之间。根据斜率决定。
这里我们假设长轴是x,如上图,每次x递增1时,y轴根据斜率判断增加的值,如果大于0.5时,则代表了线段的y值是在右上的格子(y+1),小于0.5表示线段的y值是在右边的格子(y不变)
由此可以根据斜率判断每次x递增时,y轴的值是否需要+1
循环内省去了除法计算,减少了浮点数计算
float t = (x - x0) / (float)(x1 - x0);
int y = y0 * (1. - t) + y1 * t;
void line(int x0, int y0, int x1, int y1, TGAImage &image, TGAColor color) { bool steep = false; if (std::abs(x0-x1)<std::abs(y0-y1)) { std::swap(x0, y0); std::swap(x1, y1); steep = true; } if (x0>x1) { std::swap(x0, x1); std::swap(y0, y1); } int dx = x1-x0; int dy = y1-y0; float derror = std::abs(dy/float(dx)); float error = 0; int y = y0; for (int x=x0; x<=x1; x++) { if (steep) { image.set(y, x, color); } else { image.set(x, y, color); } error += derror; if (error>.5) { y += (y1>y0?1:-1); error -= 1.; } }
}
问题:
仍然还有一个浮点数计算及比较
error += derror;
第五次尝试
error浮点数在循环体中的作用就是来用与0.5做大小比较
error += derror;
if (error > .5)
error -= 1.;
==>> error每次变化量都乘2
error += derror * 2;
if (error > 1)
error -= 2;
==>> error每次变化量都乘dx
error += derror * 2 * dx;
if (error > dx)
error -= 2 * dx;
==>> derror * 2 * dx 是int型 std::abs(dy)*2;
==>>error也不需要再是float
void line(int x0, int y0, int x1, int y1, TGAImage &image, TGAColor color) { bool steep = false; if (std::abs(x0-x1)<std::abs(y0-y1)) { std::swap(x0, y0); std::swap(x1, y1); steep = true; } if (x0>x1) { std::swap(x0, x1); std::swap(y0, y1); } int dx = x1-x0; int dy = y1-y0; int derror2 = std::abs(dy)*2; int error2 = 0; int y = y0; for (int x=x0; x<=x1; x++) { if (steep) { image.set(y, x, color); } else { image.set(x, y, color); } error2 += derror2; if (error2 > dx) { y += (y1>y0?1:-1); error2 -= dx*2; } }
}
消除循环中的分支
将steep判断移到for循环外,可以通过牺牲一些代码膨胀,把速度提高到2倍
(现代一些编译器会自动移出到for循环外)
if(steep) {for(int x = x0; x<=x1; ++x) {img.set_pixel_color(y, x, color);error2 += derror2;if(error2 > dx) {y += (y1>y0? 1 : -1);error2 -= dx*2;}}} else {for(int x = x0; x<=x1; ++x) {img.set_pixel_color(x, y, color);error2 += derror2;if(error2 > dx) {y += (y1>y0? 1 : -1);error2 -= dx*2;}}}
线框显示
导入了一个模型数据读取的类model.h,model.cpp和向量几何运算的类geometry.h
obj文件的数据:
v 0.608654 -0.568839 -0.416318
其中“v "开头的数据代表了模型顶点的位置,归一化之后的。通常取值在-1,1,实际要根据自身屏幕的宽高进行转化
f 1193/1240/1193 1180/1227/1180 1179/1226/1179
"f "储存了每个面(至少是个三角形)的信息,每组数字的第一个代表了前面对”v “开头的顶点数据的索引。obj文件的索引是从1开始,因此从c++的数组读取时,索引要-1读取
for (int i=0; i<model->nfaces(); i++) { std::vector<int> face = model->face(i); for (int j=0; j<3; j++) { Vec3f v0 = model->vert(face[j]); Vec3f v1 = model->vert(face[(j+1)%3]); int x0 = (v0.x+1.)*width/2.; int y0 = (v0.y+1.)*height/2.; int x1 = (v1.x+1.)*width/2.; int y1 = (v1.y+1.)*height/2.; line(x0, y0, x1, y1, image, white); }
}
我这里给model加了个maxNum,用来适配obj顶点数据是非标准化设备坐标



项目跟随练习代码地址
这篇关于tinyrenderer-Bresenham绘制直线算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







