数的大家庭——虚数和复数的由来

本文主要是介绍数的大家庭——虚数和复数的由来，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

数的发展

引入虚数

数的发展

数的发展也是源自于生活（何为源自生活？比如：数羊，一只羊是“羊”、二只羊是“羊羊”、三只羊是“羊羊羊”等等àà用石头代替羊的方法，一只羊是“一个石头”、二只羊是“二个石头”、三只羊是“三个石头”等等àà用刻痕的方法），所以，最早时期，数与生活是离不开的，数就是用来表示自然中的事物的个数的（所以，最早的数就叫自然数？）。每个地方数的写法不一样，有罗马数、有阿拉伯数。那么“0”算不算自然数？长期有争论，现在的教材中规定：“0”是自然数（代表没有也是自然的一种状态？）。在2000年前，教材中的“0”还不算自然数；在数论中，0也不算自然数。

数的发明，极大的方便的生活（如果没有数，表示100只羊，得用“羊羊羊……”），理论上，就算是有了数字，如果要表示100也得用100个不一样的数，但是，人类发明了“进制”。有了自然数，很快有了四则运算“加减乘除”，1+2=3，那么1-2=？，后来，发明负数。1*2=3，那么1/2=？，后来，发明分数。（此时，数的概念与日常生活逐渐剥离了，单纯为了研究而研究，比如：“5”不一定是得代表5只羊，也就是数学已经变成了一种工具【既然是工具，就可以在逻辑的基础上去扩充它，完善它】）

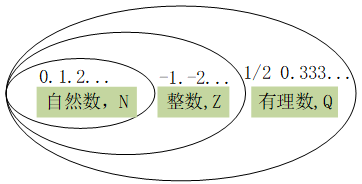
至此，早期人们认为，此时，数已经比较完整了，古希腊时期的毕达哥拉斯学派他们就信奉“数即万物”（即，宇宙中的所有事物都可以用整数或者整数之比来表示），直到有一天，毕达哥拉斯学派有一个人叫希帕索斯，发现，边长为1的正方形无法用两个整数表示，希帕索斯被同伴扔进海里（第一次数学危机）；后来，人们才发现，在一个数轴上还有很多不能用整数表示的数，比如，e，π，2等等，后来称之为无理数，所以，数集又被扩充了，有理数+无理数=实数。

实数R，是连续的，否则微积分就没法用了，同时，数据体系也会受到威胁；

引入虚数

虚数到底有什么意义呢？数，没必要非得有意义！！！（如：π，e）,虚数也是一样的，人们创造虚数就是为了让数学的逻辑更加完善。何为逻辑更加完善？如：一无二次方程ax2+bx+c=0，a≠0的解的一般表达式为。

一开始，Δ＜0时，人们认为这是无法开根号的（就像一开始人们无法接受1减2一样，负数，其实到17世纪才开始被人们接受），既然数学是一种工作，那么，就得努力去想办法表达，而不是只告诉你此路不通，所以，当Δ＜0时，人们就引入了一个虚数单位i（就是人为规定，物理学中经常用j表示，与电流i区分，并且定义 “I2=-1”，）方程组也人两个组，即逻辑更加完善。