虚数专题
数学中的虚数单位 i 和电学中的虚数单位 j
什么是虚数? 虚数是扩展实数概念的一类数,能够解决某些在实数范围内无法解决的问题。虚数的基本单位是 (i),定义为: i = − 1 i = \sqrt{-1} i=−1 这意味着 (i) 的平方是 -1: i 2 = − 1 i^2 = -1 i2=−1 为什么需要虚数? 在数学中,有些方程在实数范围内没有解。例如,方程 (x^2 + 1 = 0) 在实数范围内没有解,因
信号傅里叶变换后的实数和虚数部分理解
傅里叶(FFT、DFT、傅立叶、Fourier)傅里叶变换的结果为什么含有复数? 为什么傅里叶变换的结果含有复数成份? 看了很多关于FFT的资料,现在看到一个资料说FFT转换的结果是实部+虚部,所以不理解为什么从时域转到频域就会变成复数。 第一,从定义式上看,积分号里含有复数,积分结果是复数; 第二,从傅立叶变换的物理意义上看:FT变换是将一个信号分解为多个信号之和的形式,并且是正弦或余弦信号
虚数到底有什么意义?从 i 说起
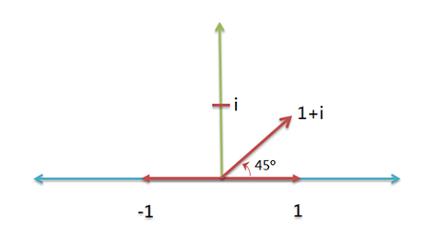
有人在Stack Exchange问了一个问题: "我一直觉得虚数(imaginary number)很难懂。中学老师说,虚数就是-1的平方根。 可是,什么数的平方等于-1呢?计算器直接显示出错! 直到今天,我也没有搞懂。谁能解释,虚数到底是什么?它有什么用?" 帖子的下面,很多人给出了自己的解释,还推荐了一篇非常棒的文章《虚数的图解》。我读后恍然大悟,醍醐灌顶,原来虚数这么简单,一点
数学中的各种符号虚数概念
max i∈SA i ≥ ∑ i∈SB i. 这个不等式表达的意思是对于集合 S 中的任意非空子集,子集中的最大的 A_i(A 的元素)的值都大于等于子集中所有 B_i(B 的元素)的值的总和。换句话说,集合 S 中的最大的 A 值至少要大于等于集合 S 中所有 B 值的总和。 此外,数学中还有许多符号(我原来也不知道): 数学中有许多符号,这些符号在数学表达中起着重要的作用。以
数的大家庭——虚数和复数的由来
目录 数的发展 引入虚数 数的发展 数的发展也是源自于生活(何为源自生活?比如:数羊,一只羊是“羊”、二只羊是“羊羊”、三只羊是“羊羊羊”等等àà用石头代替羊的方法,一只羊是“一个石头”、二只羊是“二个石头”、三只羊是“三个石头”等等àà用刻痕的方法),所以,最早时期,数与生活是离不开的,数就是用来表示自然中的事物的个数的(所以,最早的数就叫自然数?)。每个地方数的写法不一样,
闲话复数(1) | 不现实的虚数 i 为什么虚?它长成什么样?
原文 | https://mp.weixin.qq.com/s/y-Nb3S508UZuf_0GtRuNaQ 复数的英文是complex number,直译是复杂的数。最早接触复数大概是在高中时期,只知道复数由实部和虚部组成,虚部用i表示,i2=-1。天啊,无限不循环的无理数勉强可以接受,这个i到底是个什么东西?相比实数而言,这个不现实的虚数为什么虚?它长成什么样? 虚数的诞生
matlab对负数开立方根得到虚数的解决方案
问题描述:在matlab中,对负数开立方根,不出意外你将得到虚数。 例如 − 27 3 \sqrt[3]{-27} 3−27 ,我们知道其实数解是-3,但在matlab中的计算结果如下: 问题原因:matlab中的立方根运算是在复数域进行的,有3个,而matlab取的是辐角最小的那个。 解决方案:最小辐角是 π 3 \frac{\pi}{3} 3π,相邻两立方根辐角之差为 2 π
为什么虚数不能比较大小呢?
解释一:(比较形象) 虚数是利用虚轴和实轴来表示的, 类似在平面坐标系内的点,只有位置,没有大小。 就象坐在电影院里的两个人,不存在座位上的大小关系。 解释二:(比较民主) 数学上面的大小,其实是人为规定的一个定义,比如我们规定:在数轴上,右边的比左边的大。这样1就比-1大。反过来定义,在数学上也没什么问题,不过和实际生活中的使用,就乱掉了。所以一维情况,刚好是数学上
浅谈虚数i在电路分析中的作用
虚数在我们的电子电路中应用非常广泛,从电路分析的向量法,数字信号处理的FFT运算,还有多阶微分 方程的求解等等,然而,虚数的出现,正式我开始迷惑的时候,以前,我们只知道虚数 i的平方=-1,然而后来 从容抗1/jWC,感抗jWL,到后来的各种复杂公式,都带上了虚数,这让我迷惑,而我的大学老师并没有解释这 些出来的原由,我相信很多的朋友跟我也有类似的经历,也许现在的老师授课更偏重于应用而非原理