浅谈虚数i在电路分析中的作用

虚数在我们的电子电路中应用非常广泛，从电路分析的向量法，数字信号处理的FFT运算，还有多阶微分

方程的求解等等，然而，虚数的出现，正式我开始迷惑的时候，以前，我们只知道虚数 i的平方=-1，然而后来

从容抗1/jWC，感抗jWL，到后来的各种复杂公式，都带上了虚数，这让我迷惑，而我的大学老师并没有解释这

些出来的原由，我相信很多的朋友跟我也有类似的经历，也许现在的老师授课更偏重于应用而非原理，但是在

从事专业行业的朋友都知道，正式理论的不足，才造成了我们技能的瓶颈。所以，我觉得还是有必要讨论一下：

虚数之所以简称 i ，是因为他的英文 image （想象），从字面上就可以看出来，这个数字的开始，是数学家

假象出来的，他在出生最初的一些年里面，并没什么发展，知道后来，然们才开始发现他的魅力。

我们知道，在电路和电磁波理论里面 ，函数的模型都是正弦和余弦函数，因为他们的积分和微分都还是正弦

和余弦函数，被称作最简单的函数模型，傅里叶级数提出，任何信号（当然要符合一些收敛条件）都能分解成无

限频率的正弦函数的叠加，因此，我们在电路中的计算，就相当于是正弦和余弦函数的计算，一个正弦或余弦函数，

包括 幅度 ，频率 ，和相位这三个信息 ，在大量的计算中是稍显困难的，通常，我们在进行一个运算时，会进行一

些变换，比如等号两端先同时微分，计算后再积分，或者用几何法来代替代数法等等。同理，科学家们也找到了一个

适合正弦函数的计算方式。在这方面，虚数就表现的更好。

这里我们要用到一个伟大的公式：欧拉公式    e^ix=cosx+isinx 

欧拉公式和他的变换式将正弦和余弦函数转化为指数函数，指数函数在乘法和除法的运算中非常简便，虽然

在现实中并不存在i ，但是我们通过这种数学的变换能更快速的解答问题，这就是我们用i的目的。

下面我们看一下i的魅力（斜体字为转载）： 

首先，假设有一根数轴，上面有两个反向的点：+1和-1。

这根数轴的正向部分，可以绕原点旋转。显然，逆时针旋转180度，+1就会变成-1。

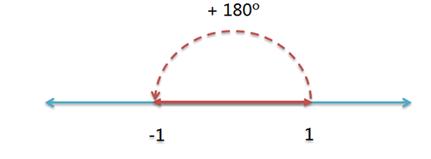
这相当于两次逆时针旋转90度。

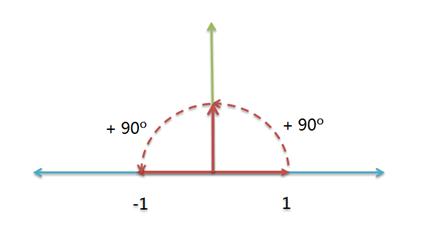
因此，我们可以得到下面的关系式：

　(+1) * (逆时针旋转90度) * (逆时针旋转90度) = (-1)

如果把+1消去，这个式子就变为：

(逆时针旋转90度)^2 = (-1)

将"逆时针旋转90度"记为 i ：
i^2 = (-1)

这个式子很眼熟，它就是虚数的定义公式。
所以，我们可以知道，虚数 i 就是逆时针旋转90度，i 不是一个数，而是一个旋转量。

既然 i 表示旋转量，我们就可以用 i ，表示任何实数的旋转状态。

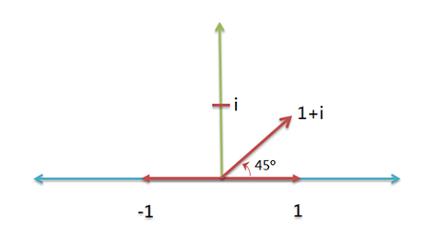
将实数轴看作横轴，虚数轴看作纵轴，就构成了一个二维平面。旋转到某一个角度的任何正实数，必然唯一对应这个平面中的某个点。

只要确定横坐标和纵坐标，比如( 1 , i )，就可以确定某个实数的旋转量（45度）。

数学家用一种特殊的表示方法，表示这个二维坐标：用 + 号把横坐标和纵坐标连接起来。比如，把 ( 1 , i ) 表示成 1 + i 。这种表示方法就叫做复数（complex number），其中 1 称为实数部，i 称为虚数部。

这样，对于一个复数，我们可以用旋转量表示余弦函数的相位，用模表示余弦函数的幅值。

这里要提到（在复数域的变换中，变换后的函数并不等于原函数，因为复数只是人们想象的数，

但是在经过一些运算后，复数的一些值，和原函数计算后的值是存在确定关系的，我们经过反

变换就可得到想要的值，这就是我们使用复数的意义）