【运筹优化】子集和问题（Subset Sum Problems , SSP）介绍 + 动态规划求解 + Java代码实现

本文主要是介绍【运筹优化】子集和问题（Subset Sum Problems , SSP）介绍 + 动态规划求解 + Java代码实现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

一、问题介绍
二、动态规划求解思路
三、Java代码实现

一、问题介绍

子集和问题（Subset Sum Problems , SSP），它是复杂性理论中最重要的问题之一。

SSP会给定一组整数 $a_1,a_2,....,a_n$ ，最多 $n$ 个整数，我们需要判断是否存在一个非空子集，使得子集的总和为 $M$ 整数？如果存在则需要输出该子集。

例如，集合给定为 $[5, 2, 1, 3, 9]$ ，子集之和为 $9$ ；答案是肯定的，因为子集 $[5, 3, 1]$ 的总和等于 $9$ 。

这是一个 $NP$ 完全问题。是背包的特殊情况。

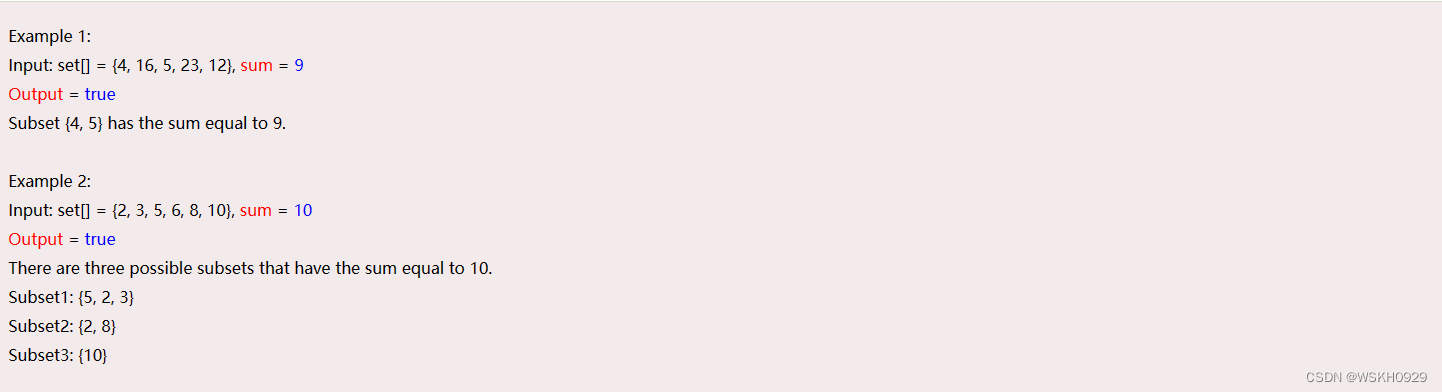
在这里插入图片描述

目的：给定一组正整数和一个值 S 总和，找出数组中是否存在一个子集，其总和等于给定的总和 S。

二、动态规划求解思路

设 A 是包含“n”个非负整数的数组或集合。找到集合“A”的子集“x”，使得 x 的所有元素的总和等于 w，其中 x 是另一个输入（总和）。

例如：

A = [2， 3， 5， 7， 10]

总和（w） = 14

首先，我们创建一个表。该列包含从 0 到 14 的值，而行包含给定集合的元素，如下所示：

在下表中：

i ：它表示行。行表示元素。

j ：它表示列。列表示总和。

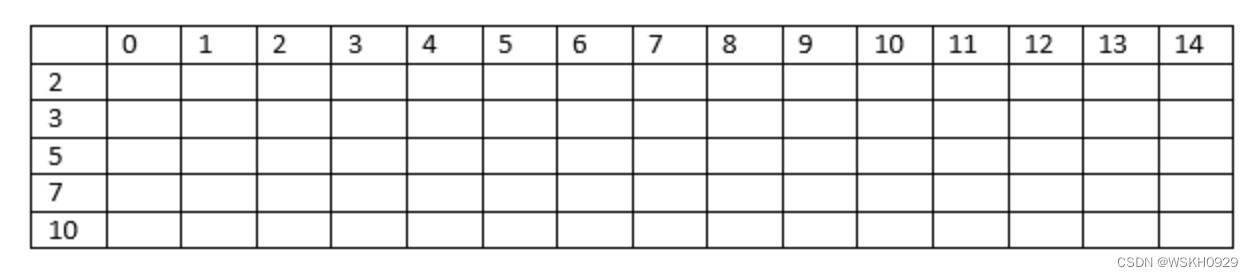
在这里插入图片描述
我们将使用 1 作为真值，使用 0 作为假值。值 1 位于 0 和 2 列下，如下所示：

这里 i=1， a[i] =2

注：每列的填充规则如下：
所需总和 = j - 元素
A[i][j] = A[i-1][所需总和]

当 j = 1

所需总和 = 1 - 2 = -1;由于总和为负，因此如上表所示，在第 1 列下输入 0。

当 j = 2

所需总和 = 2 - 2 = 0;由于 sum 的值为零，因此我们将 1 放在第 2 列下，如上表所示。

我们将 0 放在总和大于 2 的列下，因为我们不能从元素 2 中得出总和超过 2。

考虑要素 3。

这里 i = 2， a[i] = 3

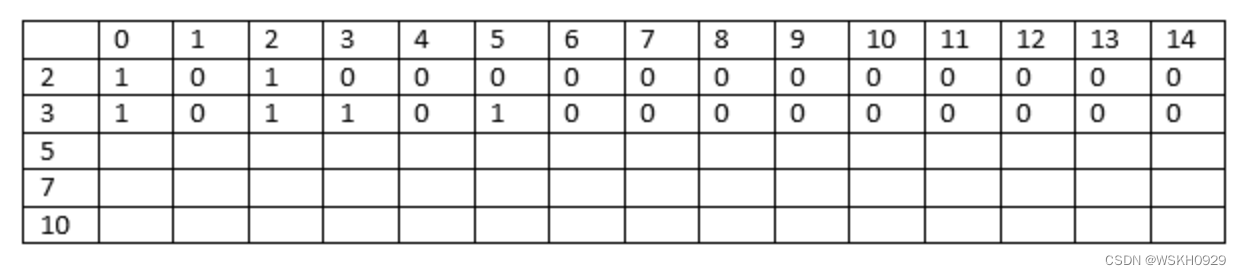
在这里插入图片描述
总和小于 3 的列将具有与前几列相同的值。

当 j = 3 时，总和 [j] = 3

所需总和 = 3 -3 = 0;由于总和为零，因此我们将 1 放在第 3 列下，如上表所示。

当 j = 4;总和[j] = 4

所需总和 = 4 - 3 = 1;由于总和为 1，因此我们移至前一行，即 i=1 和 j=1。a[1][1] 处的值为 0，因此我们将 0 放在 a[2][4] 处。

当 j = 5 时，总和 [j] = 5

所需总和 = 5 -3 = 2;sum 的值为 2，因此 a[1][2] 处的值等于 1。因此，a[2][5] 处的值将为 1。

当 j = 6 时，总和 [j] = 6

所需总和 = 6 -3 = 3;sum 的值为 3，因此 a[1][3] 处的值等于 0。因此，a[2][6] 处的值将为 0。

当 j = 7 时，总和 [7] = 7

所需总和 = 7 - 3 = 4;sum 的值为 4，因此 a[1][4] 处的值等于 0。因此，a[2][7] 处的值将为 0。

这样，我们从第 8 列到 14 列中获取值 0。

考虑要素 5。

这里 i=3， a[i] = 5

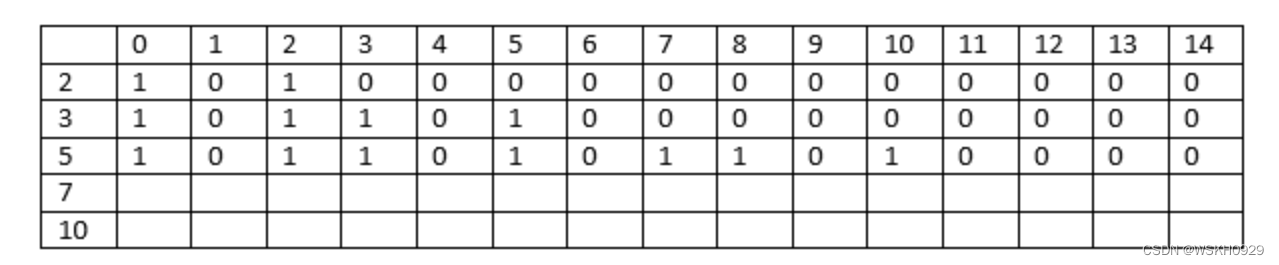
在这里插入图片描述
总和小于 5 的列将具有与前几列相同的值。

当 j = 5 时，总和 [j] = 5

所需总和 = 5-5 = 0;由于总和的值为 0;因此，A[2][5] 处的值等于 1。

当 j = 6 时，总和 [j] = 6

所需总和 = 6-5 = 1;sum 的值为 1，因此 a[2][1] 处的值等于 0;因此，a[3][6] 处的值等于 0。

当 j=7 时，总和 [j] = 7

所需总和 = 7-5 = 2;sum 的值为 2，因此 a[2][2] 处的值等于 1;因此，a[3][7] 处的值等于 1。

当 j=8 时，总和 [j] = 8

所需总和 = 8-5 = 3;sum 的值为 3，因此 a[2][3] 处的值等于 1;因此，a[3][8] 处的值等于 1。

当 j=9 时，总和 [j] =9

所需总和 = 9-5 = 4;sum 的值为 4，因此 a[2][4] 处的值等于 0;因此，a[3][9] 处的值等于 0。

这样，我们从第 10 列到 14 列中获取值。

考虑要素 7。

这里 i=4， a[i] =7

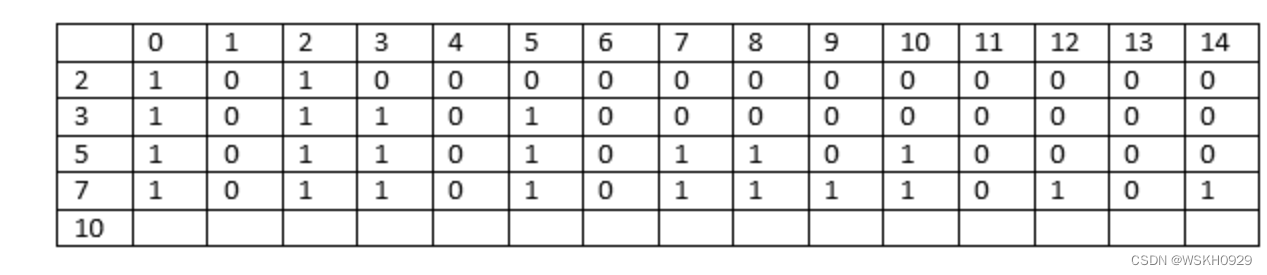
在这里插入图片描述
总和小于 7 的列将具有与前几列相同的值。

当 j=9 时，总和 [j] = 9

所需总和 = 9 - 7 = 2;sum 的值为 2，因此 a[3][2] 处的值等于 1;因此，a[4][9] 处的值等于 1。

当 j=10 时，总和 [j] = 10

所需总和 = 10 - 7= 3;sum 的值为 3，因此 a[3][3] 处的值等于 1;因此，a[4][10] 处的值等于 1。

当 j=11 时，总和 [j] =11

所需总和 = 11-7 = 4;sum 的值为 4，因此 a[3][4] 处的值等于 0;因此，a[4][11] 处的值等于 0。

当 j=12 时，总和 [j] = 12

所需总和 = 12-7 = 5;sum 的值为 5，因此 a[3][5] 处的值等于 1;因此，a[4][12] 处的值等于 1。

当 j=13 时，总和 [j] =13

所需总和 = 13 - 7 = 6;sum 的值为 6，因此 a[3][6] 处的值等于 0;因此，a[4][13] 处的值等于 0。

当 j=14 时，总和 [j] = 14

所需总和 = 14 - 7 = 7;sum 的值为 7，因此 a[3][7] 处的值等于 1;因此，a[4][14] 处的值等于 1。

考虑元素 10

这里 i=5， a[i] = 10

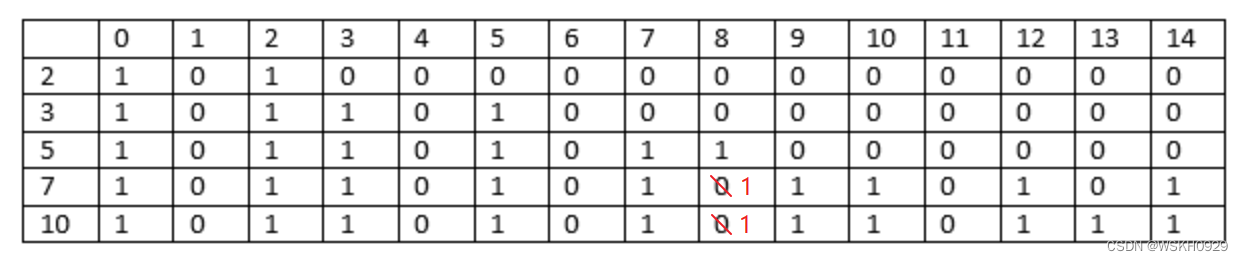
在这里插入图片描述

总和小于 10 的列将具有与前几列相同的值。

当 j = 10 时，总和 [j] = 10

所需总和 = 10 - 10 = 0;sum 的值为 0，因此 a[4][0] 处的值等于 1;因此，a[5][10] 处的值等于 1。

当 j = 11 时，总和 [j] = 11

所需总和 = 11 - 10 = 1;总和的值为 1，因此 a[4][1] 处的值等于 0;因此，a[5][11] 处的值等于 0。

当 j=12 时，总和 [j] = 12

所需总和 = 12-10 = 2;sum 的值为 2，因此 a[4][2] 处的值等于 1;因此，A[5][12] 处的值等于 1。

当 j=13 时，总和 [j] = 13

所需总和 = 13 - 10 = 3;sum 的值为 3，因此 a[4][3] 处的值等于 1;因此，a[5][13] 处的值等于 1。

为了确定上述给定的问题是否包含子集，我们需要检查最后一行和最后一列。如果值为 1，则表示至少存在一个子集。

我们基本上遵循三个条件，在表的单元格中写入 1：
• A[i] = j
• A[i-1][j] = 1
• A[i-1][j-A[i]] = 1

三、Java代码实现

测试案例

A = {2, 3, 5, 7, 10}
sum = 14

Java代码

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;/*** @Author：WSKH* @ClassName：SSP_DP* @ClassType：* @Description：* @Date：2022/12/18/18:42* @Email：1187560563@qq.com* @Blog：https://blog.csdn.net/weixin_51545953?type=blog*/
public class SSP_DP {public static void main(String[] args) {int sum = 14;int[] arr = new int[]{2, 3, 5, 7, 10};long s = System.currentTimeMillis();new SSP_DP().solve(arr, sum);System.out.println("用时: " + (System.currentTimeMillis() - s) / 1000d + " s");}static int totalWei = 32;static int arrLength;public void solve(int[] arr, int sum) {// 如果sum=0直接返回空集if (sum == 0) {System.out.println(new ArrayList<>());return;}// 深拷贝数组arr = arr.clone();// 升序排序数组Arrays.sort(arr);SubSolution[] dp = new SubSolution[sum + 1];arrLength = arr.length;for (int rowIndex = 0; rowIndex < arr.length; rowIndex++) {if (arr[rowIndex] > sum) {break;}// 遍历上一层除了0位置外，有1的位置if (rowIndex > 0) {for (int colIndex = sum - arr[rowIndex]; colIndex >= 1; colIndex--) {if (dp[colIndex] != null) {if (dp[colIndex + arr[rowIndex]] == null) {dp[colIndex + arr[rowIndex]] = new SubSolution(dp[colIndex].flag, rowIndex);}}}}// 将刚好等于的位置赋值if (dp[arr[rowIndex]] == null) {dp[arr[rowIndex]] = new SubSolution(rowIndex);}for (SubSolution subSolution : dp) {System.out.print((subSolution == null ? 0 : 1) + ",");}System.out.println();}if (dp[sum] != null) {int checkSum = 0;List<Integer> valueList = new ArrayList<>();for (int i = 0; i < arr.length; i++) {if ((dp[sum].flag[i / totalWei] & (1 << (i % totalWei))) != 0) {valueList.add(arr[i]);checkSum += arr[i];}}if (checkSum != sum) {throw new RuntimeException(valueList + " 的和不等于 " + sum);}System.out.println(valueList);} else {System.out.println(Arrays.toString(arr) + "中,没有和为" + sum + "的子集");}}public static class SubSolution {int[] flag;public SubSolution() {flag = new int[arrLength / totalWei + 1];}public SubSolution(int index) {flag = new int[arrLength / totalWei + 1];flag[index / totalWei] = (flag[index / totalWei] | (1 << index % totalWei));}public SubSolution(int[] flag, int index) {this.flag = flag.clone();this.flag[index / totalWei] = (this.flag[index / totalWei] | (1 << index % totalWei));}}}

输出

0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,1,1,0,1,0,0,0,0,0,0,0,0,0,
0,0,1,1,0,1,0,1,1,0,1,0,0,0,0,
0,0,1,1,0,1,0,1,1,1,1,0,1,0,1,
0,0,1,1,0,1,0,1,1,1,1,0,1,1,1,
[2, 5, 7]
用时: 0.002 s