压缩感知测量矩阵之有限等距常数RIC的计算

本文主要是介绍压缩感知测量矩阵之有限等距常数RIC的计算，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

有限等距常数（RestrictedIsometry Constant, RIC）是与有限等距性质（Restricted IsometryProperty, RIP）紧密结合在一起的一个参数。在前面的一篇《压缩感知测量矩阵之有限等距性质》中已经给出了RIC的定义【1】：

S阶RIP性质只要要求0<δ_S<1就可以了，而RIC是指满足RIP的最小δ_S。

在网上偶然搜到了一个计算RIC的MATLAB程序【2】，从这个程序可以理解有关RIC深层次的一些关系，加深概念的理解，代码如下：

function y=RIPText(x,t)
% calculete the kth Restricted Isometry Constant of measurement matrix x.
% Modified on March 13th, 2012.
% Reference: Wei Dai, Olgica Milenkovic. Subspace Pursuit for Compressive Sensing
% Signal Reconstruction. IEEE Trans. ona Information Theory. vol.55, no.5,
% 2230-2249. May, 2009
%calculate the Restricted Isomentry Constant of matrix constructed by
%random n columns of the original matrix x.
%created by Li Bo in March 16th, 2011
%Harbin Institute of Technolgy
n=size(x,2);%the numbers of column of original matrix x
Num=1:n;%create a row of numbers from one to n with iterval 1
Com=combntns(Num,t);% all the combination of the selected t columns from total n columns
ma=size(Com,1);% the number of combinations
delta=zeros(1,ma);% a vector used to store the restricted isometry constant candidate
for i=1:mab=x(:,Com(i,:));% new matrix constructed by the t selected columns e=eig(b'*b-eye(t));%calculate all the eigen values of matrix b'*b-eye(t)delta(i)=(max(abs(e)));%select the largest absolute eigen value as restricted isomentry candidate
end
y=max(delta);% select the largest one as restricted isometry constant

首先给出这个程序的参考文献有关RIC的部分【3】：

文献【4】更是以定理的形式给出了特征值与RIC的关系，如下定理1所示，并对定理进行了充要性的证明。

虽然程序作者已经对程序进行了详细的注释，但这里还是得再说明一下，否则初学者想看懂这个程序还是有一定难度的，下面本人对网上这个MATLAB程序进行一下解释。

1、输入输出参数

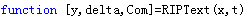
输入参数x即为待求RIC的测量矩阵即文献【1】中的F、文献【3】中的Φ、文献【4】中的A，输入参数t即文献【1】中的S、文献【3】【4】中的k；输出参数y即所求的有限等距常数RIC，另两个参数现不予解释。

2、参数初始化

第一行是使用函数size获得矩阵x的列数；第二行生成一个行向量；第三行使用了函数combntns，是得到从向量Num中任取t个值的所有组合形式，如：

如上图所示，结果将每种组合放一行，共有多少种组合就有多少行，这一步的目的是为后面任取矩阵x的t列做准备的；第四行是得到Com的行数，即得到共有多少种t列的组合；第五行成生一个全零的列向量，长为ma即组合种数。

3、主循环部分

这是整个程序最关键的部分，循环的目的是遍历每一种t列的组合，循环内部共三行。第一行是根据矩阵Com的第i行指示着取出x中的t列即其中的一种t列组合。第二行是本程序的核心，最为关键，首先函数eig是求矩阵的特征值，特征值的定义参见一般的线性代数教材，如文献【5】：

其中b’*b即为文献【4】中的G(A_T)，也就是A_T所谓的格拉姆矩阵，有关格拉姆矩阵的概念可参见文献【6】和【7】，在这里就不多说了，只知道它等于矩阵的转置乘以矩阵本身就可以了；eye(t)生成一个单位矩阵，即对角线元素全为1其它元素全为零的矩阵；然后eig(b'*b-eye(t))所求得的特征值是b'*b特征值减去1，这个可以证明：

设矩阵A的特征值为λ_A，即Ax=λ_Ax，根据特征值的定义知道单位阵的特征值为1，所以根据特征值定义有

(A－E)x=λx=Ax－Ex=λ_Ax－x=(λ_A－1) x

以上面文献【4】的符号来说明，G(A_T)的特征值在[1－δ_k, 1+δ_k]之间，那么由第二行求得的特征值应在[－δ_k, +δ_k]之间。第三行用函数max求所得特征值的最大值，即δ_k了；注意程序中的这行程序来自文献【2】的后半部分链接，其它来自前半部分链接，此句前半部分的链接程序为为delta(i)=max(e);，而我个人感觉这句话应该为delta(i)=max(abs(e));，即就求特征值最大值前应该先取绝对值，因为若求出的负值的绝对值中含大于正值最大值的项应该取更大的绝对值，就如上面文献【4】式(7)下面的那一行(下限是1减去，上限是减去1，相当于都减1再取绝对值)

δ_k =max{1－λ_min(G(A_T)),λ_max(G(A_T))－1}

经过循环后，遍历所有组合得到每一个组合的最大值。

最后一句话再用y=max(delta)取出所有组合中的最大值的最大值。

然而，要想真的用上面的程序计算一个矩阵的RIC是不现实的，因为文献【4】中又指出了这是一个组合复杂度问题：

本人在笔记本电脑上尝试了几次，当t>=8时就会报内存不足的错误：

其实主要是Com=combntns(Num,t);这行程序出了问题，原因就是这个是组合复杂度问题，因此这个程序目前来看只能是让我们更好的理解这里面复杂的关系和概念。文献【4】给出了一种计算的思路，有兴趣的可以查阅。

注：可把文献【2】的两段程序都下载下来用比较软件比较一下，本程序各有所取。

参考文献：

【1】Candes E, Tao T.Decoding by linear programming. IEEE Transactions on Information Theory,2005,59(8):4203-4215.

【2】William，RIPText，www.pudn.com/tangzhe，RIP，www.pudn.com

【3】WeiDai, Olgica Milenkovic. Subspace Pursuit for Compressive Sensing Signal Reconstruction. IEEE Trans. onInformation Theory. vol.55, no.5, 2230-2249. May, 2009

【4】张波，刘郁林，王开. 稀疏随机矩阵有限等矩性质分析[J]. 电子与信息学院，2014，36(1)：169-174.

【5】同济大学数学系编. 线性代数（第五版）[M].北京：高等教育出版社，2007：117.

【6】史秀英. 格拉姆(Gram)矩阵的半正定性及其应用[J].邵阳学院学报（自然科学版），2009，6(1)：15-17.

【7】zuobinwang. Gram方阵的探讨.百度文库

这篇关于压缩感知测量矩阵之有限等距常数RIC的计算的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！