代码随想录算法训练营第二十四天|● 理论基础 ● 77. 组合（JS写法）

本文主要是介绍代码随想录算法训练营第二十四天|● 理论基础 ● 77. 组合（JS写法），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

回溯理论基础

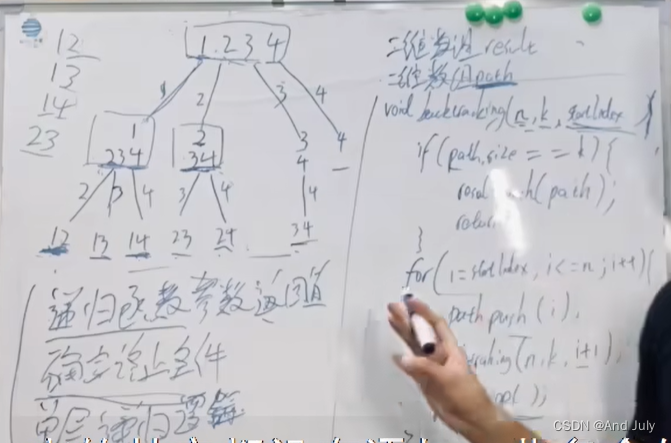
在这里插入图片描述
回溯法解决的问题都可以抽象为树形结构，因为回溯法解决的都是在集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度，都构成的树的深度。递归就要有终止条件，所以必然是一棵高度有限的树（N叉树）。

回溯三部曲

1、回溯函数模板返回值以及参数
在回溯算法中，我的习惯是函数起名字为backtracking，这个起名大家随意。回溯算法中函数返回值一般为void。
再来看一下参数，因为回溯算法需要的参数可不像二叉树递归的时候那么容易一次性确定下来，所以一般是先写逻辑，然后需要什么参数，就填什么参数。但后面的回溯题目的讲解中，为了方便大家理解，我在一开始就帮大家把参数确定下来。
回溯函数伪代码如下：

void backtracking(参数)

2、回溯函数终止条件
既然是树形结构，那么我们在讲解二叉树的递归 (opens new window)的时候，就知道遍历树形结构一定要有终止条件。所以回溯也有要终止条件。什么时候达到了终止条件，树中就可以看出，一般来说搜到叶子节点了，也就找到了满足条件的一条答案，把这个答案存放起来，并结束本层递归。所以回溯函数终止条件伪代码如下：

if (终止条件) {存放结果;return;
}

3、回溯搜索的遍历过程
在上面我们提到了，回溯法一般是在集合中递归搜索，集合的大小构成了树的宽度，递归的深度构成的树的深度。
如图：
在这里插入图片描述

回溯算法模板

void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {处理节点;backtracking(路径，选择列表); // 递归回溯，撤销处理结果}
}

77 组合

题目链接/文章讲解：https://programmercarl.com/0077.%E7%BB%84%E5%90%88.html
视频讲解：https://www.bilibili.com/video/BV1ti4y1L7cv
剪枝操作：https://www.bilibili.com/video/BV1wi4y157er
在这里插入图片描述

思路：将回溯问题理解成树，重点理解每次还要pop出来

理论上这道题如果k=2可以用两层for循环嵌套，但是如果k=50就要嵌套50层for循环，因此这时候就需要用到回溯了。（k不确定，可能很大也可能很小）
在这里插入图片描述

/*** @param {number} n* @param {number} k* @return {number[][]}*/
var combine = function(n, k) {let result = [];let path = [];//确定回溯的参数const backTracking = (n,k,start) => {//终止条件if(path.length === k){//[...path]result.push(path.slice());return;}//单层循环for(let i = start;i<=n;i++){path.push(i);backTracking(n,k,i+1);path.pop();}}backTracking(n,k,1);return result;};

使用 result.push(path.slice()) 而不是 result.push(path) 的主要原因是，JavaScript 中的数组是引用类型，如果直接使用 result.push(path)，会将 path 的引用放入 result 数组中。
由于 backtracking 过程中 path 数组不断变化（不断添加和移除元素），如果直接将 path 引用放入 result 数组中，由于 backtracking 过程中 path 数组会不断更改，最终 result 数组中的所有元素都会指向相同的 path 引用，导致 result 数组中的元素都是一样的，而不是不同的组合。
因此，为了确保在 result 数组中存储不同的组合，需要使用 path.slice() 来创建 path 的副本，将副本推入 result 数组中。这样每个组合都是不同的，不会相互影响。
所以，采用 result.push(path.slice()) 会确保在 result 数组中存储不同的组合，而不是相同的引用。

剪枝

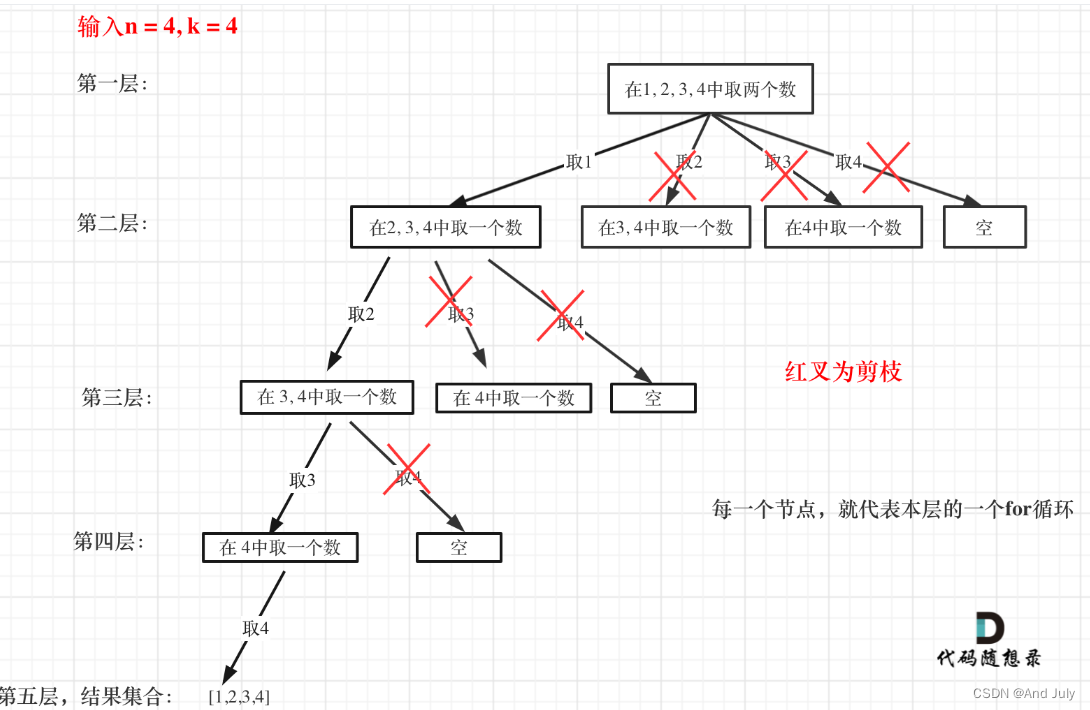
在这里插入图片描述
图中每一个节点（图中为矩形），就代表本层的一个for循环，那么每一层的for循环从第二个数开始遍历的话，都没有意义，都是无效遍历。

所以，可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。

如果for循环选择的起始位置之后的元素个数已经不足我们需要的元素个数了，那么就没有必要搜索了。

注意代码中i，就是for循环里选择的起始位置。

1、已经选择的元素个数：path.size();

2、还需要的元素个数为: k - path.size();

3、在集合n中至多要从该起始位置 : n - (k - path.size()) + 1，开始遍历

为什么有个+1呢，因为包括起始位置，我们要是一个左闭的集合。

举个例子，n = 4，k = 3，目前已经选取的元素为0（path.size为0），n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。

从2开始搜索都是合理的，可以是组合[2, 3, 4]。

因此，剪枝操作仅需要将i的范围更改即可。

/*** @param {number} n* @param {number} k* @return {number[][]}*/
var combine = function(n, k) {let result = [];let path = [];const backTracking = (n,k,start) => {if(path.length === k){//[...path]result.push(path.slice());return;}for(let i = start;i <= n - (k - path.length) + 1;i++){path.push(i);backTracking(n,k,i+1);path.pop();}}backTracking(n,k,1);return result;};