本文主要是介绍椭圆上一个动点P.问P在哪里时∠F1PF2最大的巧妙想法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
第一个巧妙的证明可能有点不严格不过还是可以看看的，囧
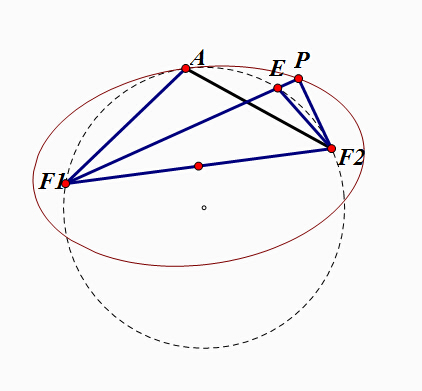
证明：作 F1AF2 的外接圆，则圆和椭圆相切（因为交于一点且有公共切线）
设 P 为椭圆上任意一点，连接
由外角大于内角知
第二个想法也很巧妙
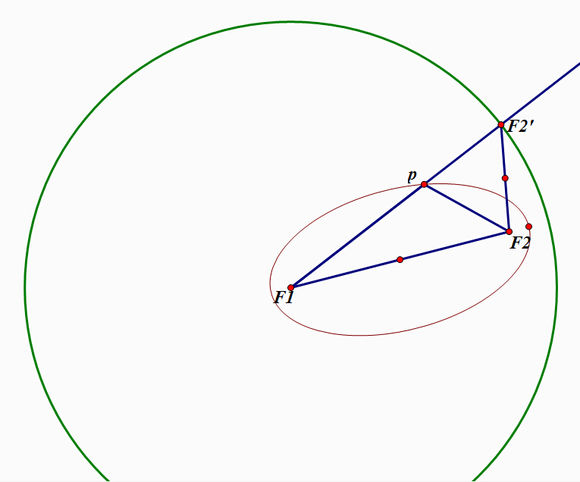
证明：连结 F1P ，作 F2 关于 F1P 的对称点 F′2 ，则 F1F2‘ 长度是定值2a，
以 F1 为原点，2a为半径作圆（如图）,注意到了吗，2 ∠F1F′2F2 = ∠F1PF2
只需求 ∠c 最大值即可
由正弦定理：
F1F2sin∠F1F′2F2=F1F2sin∠F′2F2F1=2asin∠F′2F2F1
即 sin∠F1F′2F2 =定值 ⋅sin∠F′2F2F1 （而 ∠F′2F2F1=90 度时 sin 最大，有 ∠F1F′2F2 最大，显然 ∠F1F′2F2 小于90度，保证sin单调性啦）
而 PF2F1 =90度时 F1P=F2P=PF′2
即在短轴顶点上取得最大值 证毕
液
这篇关于椭圆上一个动点P.问P在哪里时∠F1PF2最大的巧妙想法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
