Python——利用差分方程求解解偏微分方程的边值问题

1、问题

用差分方程求解下列边值问题，并编写程序：

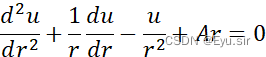
此类边值问题较为容易，我们利用差商的方法就可以求解，程序如下。 

 2、程序

选定A=B=μ=1;R=10;h=0.01;N=1000;其中h为步长。
#python
import numpy as np
import matplotlib.pyplot as plt
bg=[1001,-1000];co=[];a=0;n=1000;bh=[10];bn=[]
for j in range(999):bg.append(a)
co.append(bg)
for t in range(1001):bn.append(0)
for m in range(1000):bh.append(-(n-1)*0.000001)n=n-1
n=1000
for p in range(999):for i in range(1001):if p == i:bn[i]=1;bn[i+1]=-(2-1/(n-1)+1/((n-1)**2));bn[i+2]=1-1/(n-1)co.append(bn);bn=[]for t in range(1001):bn.append(0)n=n-1
bn=[]
for t in range(1000):bn.append(0)
bn.append(1)
co.append(bn)
A = np.array(co)
b = np.array(bh)
y = np.linalg.solve(A, b)
x=[]
for bi in range(1001):x.append(bi*0.01)
y=list(y)
y.reverse()
plt.plot(x,y,c='k',label='Value')
plt.xlabel('X');plt.ylabel('Y');plt.title('Difference Equation Solver')
plt.legend()
plt.show()

3、结果 

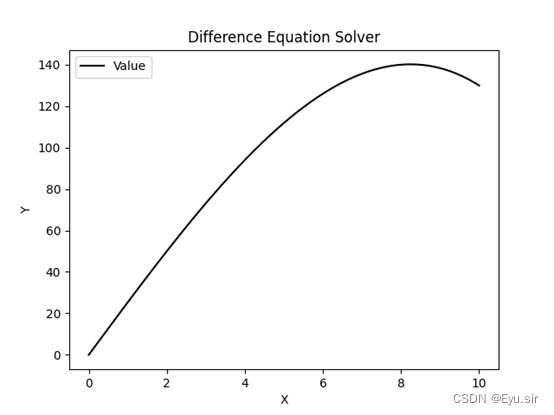
4、实验总结

（1）此类问题属于差分方程中的第二类边界条件，即边界条件有微分方程的形式出现。我们对此类微分方程的求解，主要是将其离散化，即利用一阶差分和二阶差分。

（2）算法实现的主要思想为，利用边值条件化为一阶差分，推出我们要的Ni-1项，然后将要求解的微分方程同样进行差分形式表示，即二阶差分。然后将边界条件算出的Ni=f(Ni-1),代入二阶差分，求出Ni-1=h(Ni-2)。根据这样的思想不断迭代，最后的结果就是求解一个线性方程组。我们可以使用高斯消元和赛德尔迭代法进行求解这个方程组。结果以图形可视化展示。

（3）差分法的思想和做法是,把定解区域剖分为网格,在网格结点上以差商代替微商或用某种插值方式，把微分方程化为包含有限个未知数的差分方程组。差分法直观、简易、能普遍用于各种类型的微分方程和任意形状的区域。因为它包含巨大的运算量，所以只在电子计算机问世之后，才得到广泛的应用和发展。

从微分方程出发的差分化 网格剖分的一种最简单又常用的做法是取平行于坐标轴的直线作为网格线，例如取=,=,、为步长，、取一切整数,这时网格结点为(,)。对方程(1)进行差分化、以表示差分近似解、表示在网格结点(，)上的分量。如果(,)是内结点,即邻近四个网格结点都在上,则用中心二阶差商代替二阶微商代入(1),即得相应的差分方程