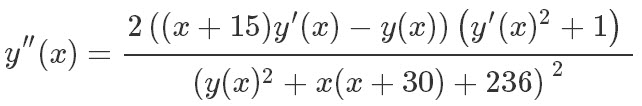边值问题专题
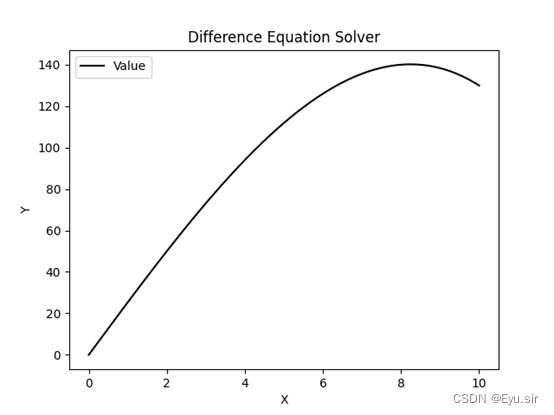
Python——利用差分方程求解解偏微分方程的边值问题
1、问题 用差分方程求解下列边值问题,并编写程序: 此类边值问题较为容易,我们利用差商的方法就可以求解,程序如下。 2、程序 选定A=B=μ=1;R=10;h=0.01;N=1000;其中h为步长。#pythonimport numpy as npimport matplotlib.pyplot as pltbg=[1001,-1000];co=[];a=
由光学到变分演变出来的二阶非线性常微分方程初边值问题
问题是这样的,如图,圆O的半径为3, 圆C半径为1; O的坐标(0,0), C坐标(-15,0), B的坐标(-14,0) 圆盘O是一个发光源,那么,如果透明介质处处的折光率都是常数, 则从B点观察圆盘O时,可以看到上边界对应于BD,下边界对应BE,都是圆O的切线; 现在假设介质的折光指数是二元函数 n(x,y) 求在这种折光指数连续变化的透明光学介质中,从B点观察发光
静电场边值问题——唯一性定理
唯一性定理的证明 已知方程组 这个方程组的解唯一 证明: 假设解不唯一,存在两个解满足 两个作差,我们可以得到 取 此时我们有 由拉普拉斯方程,我们可以得到 假设在体积内部存在极大值或者极小值,我们可以得到,这个方程不可能等于0 如果极大值极小值都在边界处出现,那么最大值最小值为0,此时恒等于0 我们得出
主要介绍了带导数的初边值问题求解思路——基于向前欧拉法以及Crank-Nicolson法
声明 本部分是一个学习笔记,主要内容来自于华冬英老师编写的《微分方程的数值解法与程序实践》。如果觉得内容不错,可自行购买价格良心的官方正版教材。http://www.hxedu.com.cn.上有配套的代码以PPT课件可供免费下载。另外,官方代码均用C语言编写,之后我也会陆陆续续上传自己编写的Python代码。 本部分内容公式太多实在懒得敲了,因此以图片形式呈现,基本能满足学习要求。不过也同时