第四十四周：文献阅读 + SG滤波+基于LSTM的编码器-解码器

本文主要是介绍第四十四周：文献阅读 + SG滤波+基于LSTM的编码器-解码器，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

摘要

Abstract

文献阅读：基于集成深度神经网络的大规模水质预测

现有问题

提出方法

方法论

Savitsky-Golay过滤器

SE-LSTM（基于LSTM的编码器-解码器神经网络）

研究实验

数据集

实验设置

评估指标

基准模型

实验结果

发展趋势

SG滤波实现

总结

摘要

本周阅读的文献《Large-scale water quality prediction with integrated deep neural network》，提出了一种基于长短期记忆的编码器-解码器神经网络和Savitzky-Golay滤波器的混合模型。其中Savitzky-Golay滤波可以消除水质时间序列中的潜在噪声，并且在去噪过程中可以很好保留数据的有效信息（特征）。而长短期记忆可以研究复杂水环境中的非线性特征，基于LSTM的编码器-解码器神经网络，能够用于处理时间序列数据中的长序列，因此可以更好地预测多步水质时间序列数据。

Abstract

The literature "Large scale water quality prediction with integrated deep neural network" read this week proposes a hybrid model based on long short-term memory encoder decoder neural network and Savitzky Golay filter. Savitzky Golay filtering can eliminate potential noise in water quality time series and effectively preserve the effective information (features) of the data during the denoising process. Long short-term memory can study nonlinear features in complex water environments, and encoder decoder neural networks based on LSTM can be used to process long sequences in time series data, thus better predicting multi-step water quality time series data.

文献阅读：基于集成深度神经网络的大规模水质预测

Large-scale water quality prediction with integrated deep neural networkhttps://doi.org/10.1016/j.ins.2021.04.057

现有问题

传统的水质预测主要基于线性模型，然而水环境条件复杂，水质时间序列中存在大量噪声，将严重影响水质预测的准确性。此外，线性模型难以处理时间序列数据的非线性关系。
传统的线性方法无法捕捉数据中的非线性特征，因此在现有的研究中，水质预测还采用了传统的支持向量机、人工神经网络、深度置信网络、堆叠自编码器等非线性方法。然而，由于数据中的噪声，这些预测模型经常遭受过拟合问题。
采用基于小波去噪技术的预测模型，有效提高了水质预测的精度。它们有效地降低了时间序列中噪声对预测精度的影响。然而，这些模型不能有效地捕捉时间序列数据的长期特征

提出方法

提出了一种基于长短期记忆的编码器-解码器神经网络和Savitzky-Golay滤波器的混合模型。其中为了解决时间序列数据的降噪问题，采用Savitzky-Golay滤波器对原始数据进行降噪，消除水质时间序列中的潜在噪声，并且SG滤波器在去噪的同时可以有效地保留时间序列的特征。而长短期记忆可以研究复杂水环境中的非线性特征。因此SE-LSTM模型可以更好地处理时间序列数据中的长序列。创新性地将Savitzky-Golay滤波器的降噪能力与LSTM的特征提取能力相结合和集成，显著提高了多步预测精度。

方法论

Savitsky-Golay过滤器

Savitzky-Golay滤波器广泛地运用于数据流平滑除噪，是一种在时域内基于局域多项式最小二乘法拟合的滤波方法也称为卷积平滑。这种滤波器最大的特点在于在滤除噪声的同时可以确保信号的形状、宽度不变。为了消除水质的频繁变化，我们使用了SG的滤波器来减少噪声的干扰，该滤波器在去噪过程中保留数据的有效信息。

SG平滑滤波的效果，随着选取窗宽不同而不同，可以满足不同场合的需求。SG卷积平滑算法是移动平滑算法的改进。关键在于矩阵算子的求解。

什么是多项式平滑？

使用五点平滑算法来说明平滑过程，把光谱一段区间的等波长间隔的5个点记为X集合，多项式平滑就是利用在波长点为 $X_{m-2},X_{m-1},X_{m},X_{m+1},X_{m+2}$ 的数据的多项式拟合值来取代 $X_{m}$ 。然后依次移动，直到把光谱遍历完。

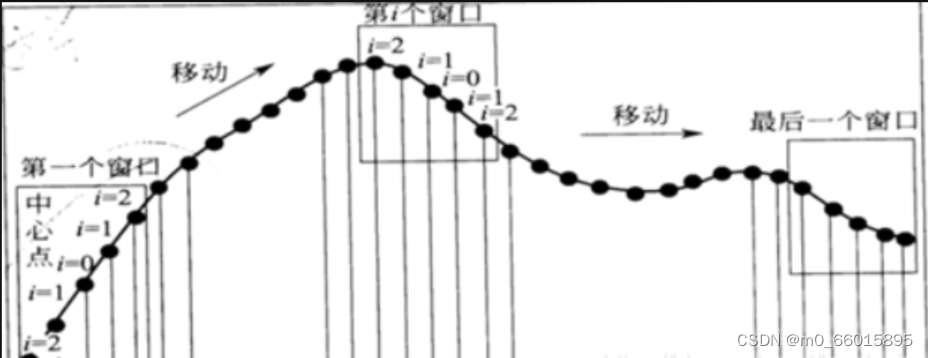
SG卷积平滑算法，用线性最小二乘法去拟合数据的每个子序列，这种方法被称为卷积。

我们经常会用一组观测数据去估计模型的参数，模型是我们根据先验知识定下的，通过一些数据分析我们猜测y和x之间存在线性关系，从而得到关于x和y的模型。很多时候没有确定解，但是我们能求出近似解，使得模型能在各个观测点上达到“最佳“拟合。最佳可以是所有观测点到直线的距离和最小，也可以是所有观测点到直线的误差（真实值-理论值）绝对值和最小，也可以是其它。

最小二乘法（又称最小平方法），它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法其实就是用来做函数拟合的一种思想，所谓“二乘”就是平方的意思。

通过矩阵法进行推导理解最小二乘法的意义：

通过几何法理解最小二乘法的几何意义：

由最小二乘法可知，Savitsky-Golay卷积平滑关键在于参数矩阵的求解，

SE-LSTM（基于LSTM的编码器-解码器神经网络）

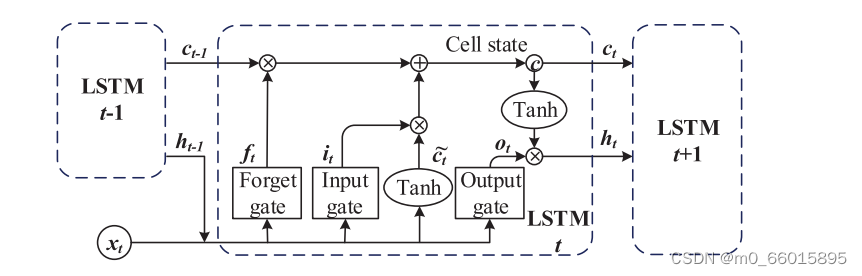
在降噪后，本文采用LSTM模型对水质进行预测。LSTM可以从重要的经验中学习，这些经验具有长期的依赖关系。LSTM的记忆细胞如图所示。

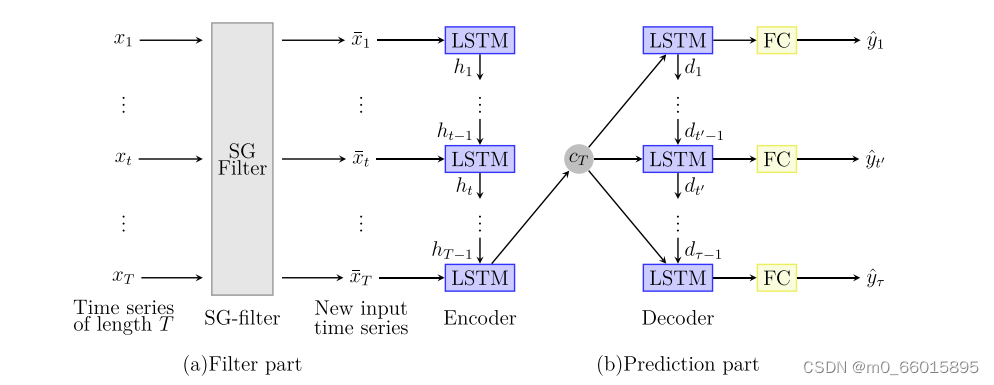
为了达到更好的预测精度，这项工作提出了一种新的编码器-解码器神经网络由过滤器部分和预测部分组成，如下图所示。采用SG滤波器降低 $\begin{Bmatrix} x_{1},...,x_{t},...,x_{T} \end{Bmatrix}$ 的输入噪声，图中的编码器是一个对输入 $\begin{Bmatrix} x_{1},...,x_{t},...,x_{T} \end{Bmatrix}$ 进行顺序变换的LSTM，然后得到从 $x_{t}$ 到 $h_{t}$ 的映射。解码器也是一个LSTM，它通过给定隐藏状态 $\begin{Bmatrix} d_{1},...,d_{t^{'}},...,d_{T-1} \end{Bmatrix}$ 获得 $\begin{Bmatrix} \hat{y}_{1},...,\hat{y}_{t^{'}},...,\hat{y}_{T} \end{Bmatrix}$ 来产生输出。LSTM能够提取时间序列的复杂特征，在多步预测中，编码器的输出 $c_{T}$ 和从解码器得到最后一步隐藏状态 $d_{T-1}$ 可以提高多步预测的性能。

模型步骤

研究实验

数据集

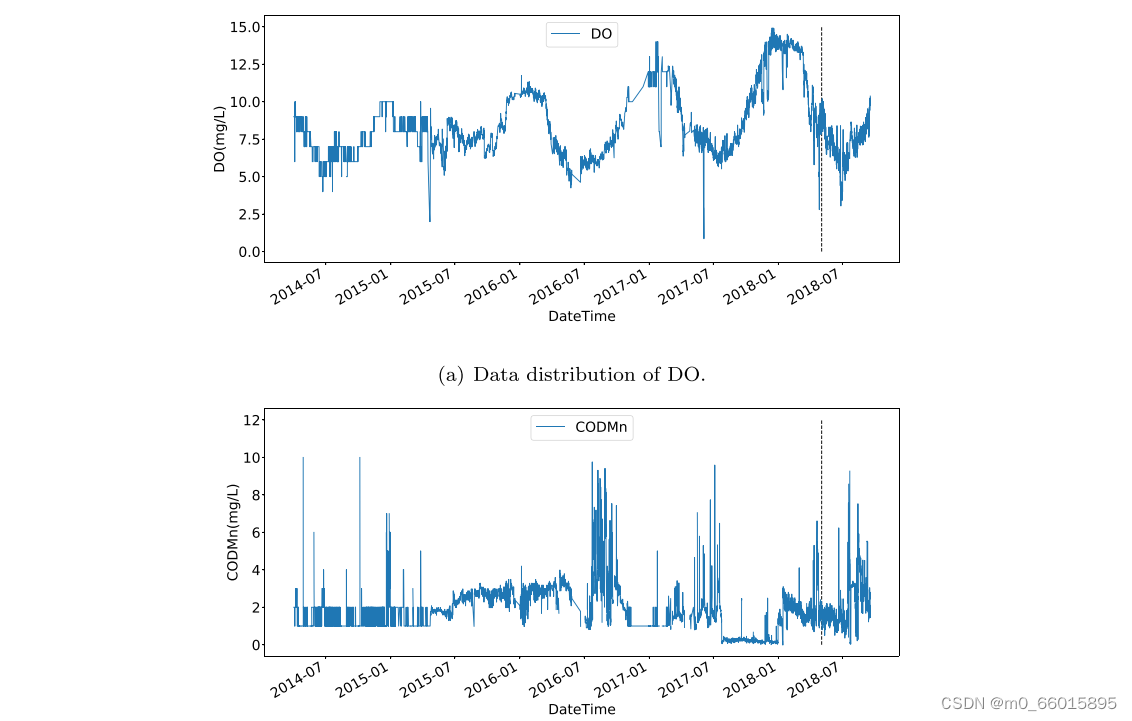
实验数据集采集自北京古北口，该数据每4小时收集一次，从2014年4月到2018年10月共收集了1万多条数据。然后将数据集分成两部分，包括训练集和测试集，比例为9:1。所有预测模型均采用溶解氧(DO)和化学需氧量(CODMn)作为实验数据。DO和CODMn的分布如图所示：

实验设置

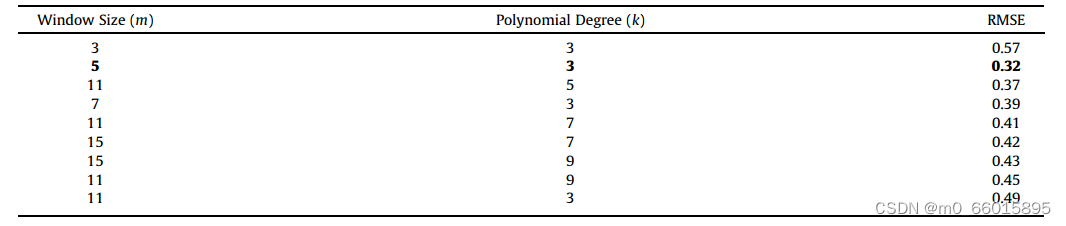
在数据预处理中，本工作采用平滑操作来消除不稳定因素，但同时也去除了原始时间序列中的一些有效信息。首先在对比实验中通过不同的窗口尺寸选择出最佳的过滤器，在原始时间序列的移动中值(MM)、SG和MA滤波器中，当窗口大小为5时三个过滤器获得最小的MSE值，并且SG滤波器的MSE值最小。

在设置SG滤波器参数中，我们给出了不同的参数设置，当窗口大小为5，即m¼5，并且k度的多项式设置为3时，获得的均方根误差(RMSE)较小。过大的窗口尺寸会去除时间特征，而过小的窗口尺寸则不能用于降噪。同样，k太大会导致最小二乘过拟合，k太小会导致欠拟合。

评估指标

为了证明SE-LSTM的预测性能，采用MAE、MAPE和RMSE三个指标来评价其预测精度。

基准模型

为了从不同方面比较所提出的方法，我们选择了几个基准模型进行比较。

ARIMA。将过去值和随机噪声通过线性函数拟合到预测值中。
ANN。人工神经网络能很好地处理非线性特征，并具有良好的预测能力。
极端梯度增强(XGBoost)。是一种通用的Tree Boosting算法，它被广泛应用于机器学习领域。首先利用树集成技术构建回归树，并将所有回归树的总得分作为最终预测值。
SVR。SVR可以通过获得最小的结构风险来提高泛化能力，在统计样本较少的情况下，也能得到较好的统计规律。
LSTM。LSTM是一种常用的序列预测模型，特别是LSTM在产生时间序列的长期依赖关系方面表现优异。为了比较LSTM和SE-LSTM的性能，实验中它们的超参数设置相同。

实验结果

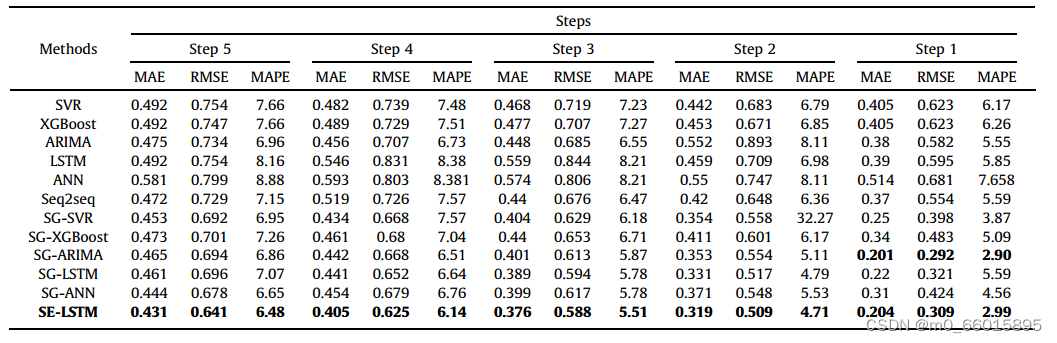
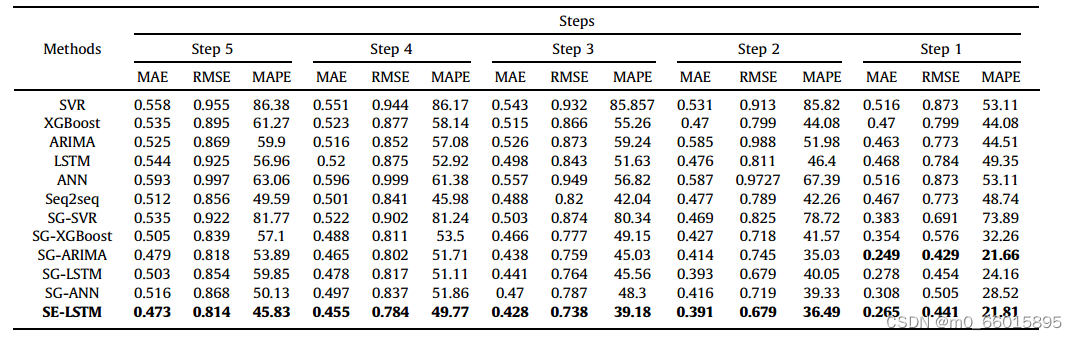
将SE-LSTM与其典型的基准测试方法进行比较，实验结果表明，传统的非线性模型与线性模型相比并没有太大的优势。这是因为水质时间序列具有较强的线性特征，线性模型具有一定的优势。此外，深度学习的预测精度优于传统模型，并且由于网络结构的变化，SE-LSTM在多步预测精度上优于SG-LSTM。此外，在加入SG滤波器后，所有模型的预测精度都得到了显著提高，验证了SG滤波器能更好地保留时间序列特征并有效去除噪声。虽然ARIMA模型在单步预测上略优于SE-LSTM模型，但SE-LSTM在多步预测上优于ARIMA模型。观察到SE-LSTM在三个指标方面优于其同行。

DO数据集的比较结果：

在CODMn数据集上的比较结果：

发展趋势

进一步改进现有模型的网络结构，使其不仅可以接收历史数据，还可以捕获相关多特征数据的输入;
将该模型应用到其他领域，例如金融时间序列和交通流，以验证其有效性和鲁棒性;
将图神经网络与时间序列模型相结合，提取水质时空特征；
从理论上研究和讨论滤波和预测模型的收敛性。

SG滤波实现

滤波函数定义，即将原理通过代码实现

void SavitskyGolaySmoothing(float *arr,int window_size, int order, int rows, int cols){#order必须要比滑动窗口要小，且滑动窗口不能为偶数if(window_size % 2 == 0){throw std::logic_error("only odd window size allowed");}if(order >= window_size){throw std::logic_error("Order must < window_size");}cv::Mat A = cv::Mat::zeros(window_size, order, CV_32FC1);cv::Mat A_T, A_INV, B;cv::Mat kernel;cv::Mat result = cv::Mat::zeros(window_size, 1, CV_32FC1);#window_size=2*step+1#order：相当于k，即得到一个order元线性方程组int step = int((window_size - 1)/2);for(int i = 0; i < window_size; i++){for(int j = 0 ; j < order; j++){#计算-step + i的j次幂float x = pow(-step + i, j);A.at<float>(i,j) = x;}}#使用了Opencv矩阵求矩阵转置和求逆A_T = A.t();   #矩阵转置 A_INV = (A_T * A).inv();   #矩阵求逆#求矩阵算子B = A * A_INV * A_T;B.row(step).copyTo(kernel);float *wrap_data = new float[step*2 + cols];for(int row =0; row < rows; row++){#扩展起始数据，大小为步长for(int n = 0; n < step; n++){wrap_data[n] = arr[row * cols];}#复制输入数据for(int col =0; col < cols; col++){wrap_data[col + step] = arr[row * cols + col];}#扩展结束数据，大小为步长for(int n = 0; n < step; n++){wrap_data[cols  + step + n] = arr[row * cols + cols -1];}for(int m = step; m < step + cols; m++){for(int n = -step, j = 0; n <=step; n++, j++){result.at<float>(0, j) = wrap_data[m + n];}arr[row * cols + m - step] = cv::Mat(kernel * result).at<float>(0 ,0);}}delete []wrap_data;}

在python下基于scipy库实现SG滤波平滑

import matplotlib.pyplot as plt
import numpy as npdef SG01(data,window_size):# 前后各m个数据，共2m+1个数据，作为滑动窗口内滤波的值m = int((window_size - 1) / 2)  # (59-1)  /2 = 29# 计算 矩阵X 的值 ，就是将自变量x带进去的值算 0次方，1次方，2次方.....k-1次方,一共window_size行，k列# 大小为（2m+1,k）X_array = []for i in range(window_size):  #arr = []for j in range(3):X0 = np.power(-m + i, j)arr.append(X0)X_array.append(arr)X_array = np.mat(X_array)# B = X*（X.T*X）^-1*X.TB = X_array * (X_array.T * X_array).I * X_array.Tdata = np.insert(data, 0, [data[0] for i in range(m)])  # 首位插入m-1个data[0]data = np.append(data, [data[-1] for i in range(m)])  # 末尾插入m-1个data[-1]# 取B中的第m行 进行拟合  因为是对滑动窗口中的最中间那个值进行滤波，所以只要获取那个值对应的参数就行， 固定不变B_m = B[m]# 存储滤波值y_array = []# 对扩充的data 从第m个数据开始遍历一直到（data.shape[0] - m）  ：（第m个数据就是原始data的第1个，（data.shape[0] - m）为原始数据的最后一个for n in range(m, data.shape[0] - m):y_true = data[n - m: n + m + 1]  # 取出真实y值的前后各m个，一共2m+1个就是滑动窗口的大小y_filter = np.dot(B_m, y_true)  # 根据公式 y_filter = B * X 算的  X就是y_truey_array.append(float(y_filter))  # float(y_filter) 从矩阵转为数值型return y_arrayif __name__ == '__main__':data = [0.3962, 0.4097, 0.2956, 0.4191, 0.3456, 0.3056, 0.6346, 0.7025, 0.6568, 0.4719, 0.5645, 0.6514, 0.5717,0.6072, 0.7076, 0.7062, 0.7086, 0.677, 0.8141, 0.7985, 0.7037, 0.7961, 0.6805, 0.5463, 0.2766]smoothed_data = SG01(data,5)smoothed_data = [round(i, 4) for i in smoothed_data]smoothed_data2 = SG01(data,11)smoothed_data2 = [round(i, 4) for i in smoothed_data2]print("data：", data)print("smoothed_data：", smoothed_data)print("smoothed_data2：", smoothed_data2)plt.plot(data, label='data')plt.plot(smoothed_data, label='smoothed_data')plt.plot(smoothed_data2, label='smoothed_data2')plt.xlabel('Time')plt.ylabel('Value')plt.title('Line Plot')plt.legend()plt.show()

总结

Savitzky-Golay平滑滤波用于数据流的平滑除噪，它的核心思想是对一定长度窗口内的数据点进行k阶多项式拟合，在不改变原有信号的形状、宽度的前提下，使得整体数据更加平滑。运用于时间序列数据预测上的优点在于，它在去除噪声的同时可以很好保留数据中包含的特征不被去除，因此可以提高预测的精度。原始的编码器-解码器结构无法捕获长期依赖关系，无法考虑过去输入的影响，而基于LSTM的基础上，可以通过记忆机制来捕捉长期依赖关系，从而实现多步预测的提升。

这篇关于第四十四周：文献阅读 + SG滤波+基于LSTM的编码器-解码器的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！