本文主要是介绍Chapter 16 Techniques of Design-Oriented Analysis: Extra Element Theorems,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Chapter 16 Techniques of Design-Oriented Analysis: Extra Element Theorems
这一章介绍Middlebrook’s Extra Element Theorem (EET), 这是一个强力的分析复杂电路传输函数的工具.
16.1 Extra Element Theorem
对于一个已知的传输函数, Extra Element Theorem可以帮助算出加入元器件的新的传输函数, 而不必从头推导.
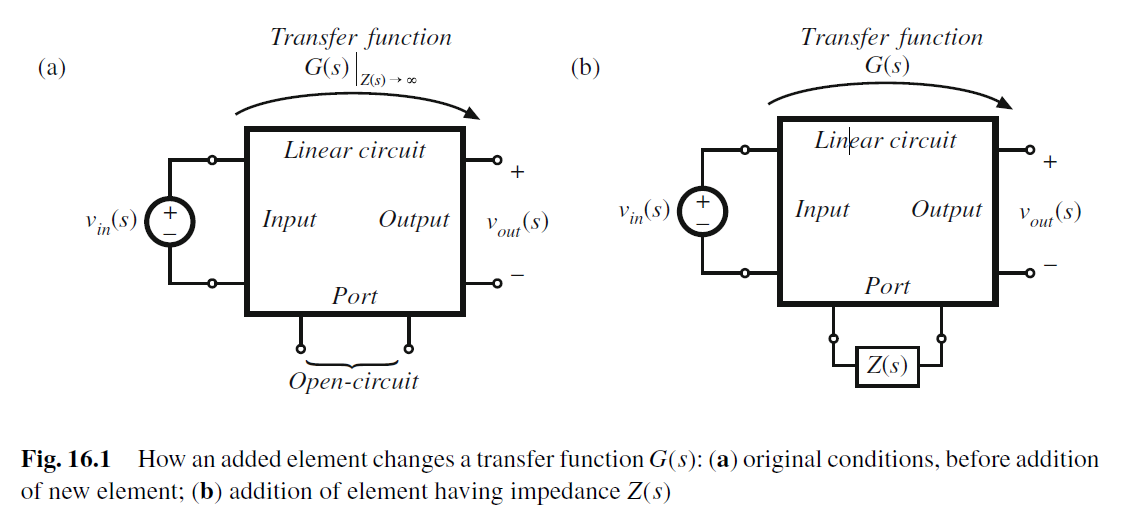
对于已知传函G0(s), 在两端添加Z(s), 新的传输函数G(s)
v o u t v i n = G ( s ) ∣ z ( s ) → ∞ ( 1 + Z N ( s ) Z ( s ) 1 + Z D ( s ) Z ( s ) ) \frac{v_{out}}{v_{in}}=G(s)\bigg|_{z(s)\to \infty }\left( \frac{1+\frac{Z_{N}(s)}{Z(s)}}{1+\frac{Z_{D}(s)}{Z(s)}} \right) vinvout=G(s) z(s)→∞ 1+Z(s)ZD(s)1+Z(s)ZN(s)
第一项为原始传输函数, 第二项为矫正因素correction factor.
类似, 对于已知传函G0(s), 断开两端添加Z(s), 新的传输函数G(s)
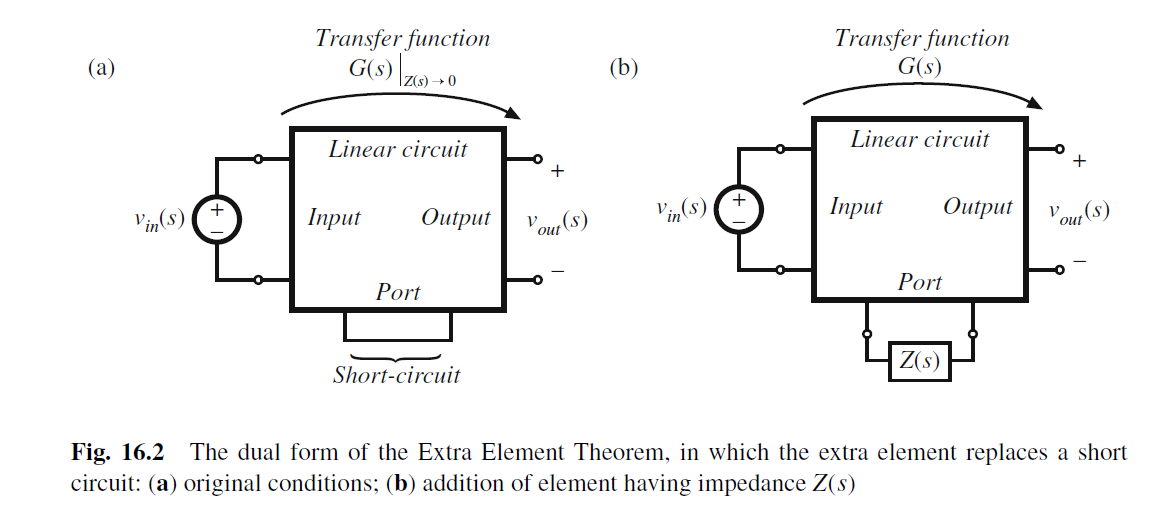
v o u t v i n = G ( s ) ∣ z ( s ) → 0 ( 1 + Z ( s ) Z N ( s ) 1 + Z ( s ) Z D ( s ) ) \frac{v_{out}}{v_{in}}=G(s)\bigg|_{z(s)\to 0}\left( \frac{1+\frac{Z(s)}{Z_{N}(s)}}{1+\frac{Z(s)}{Z_{D}(s)}} \right) vinvout=G(s) z(s)→0 1+ZD(s)Z(s)1+ZN(s)Z(s)
ZD(s)和ZN(s)的求解:
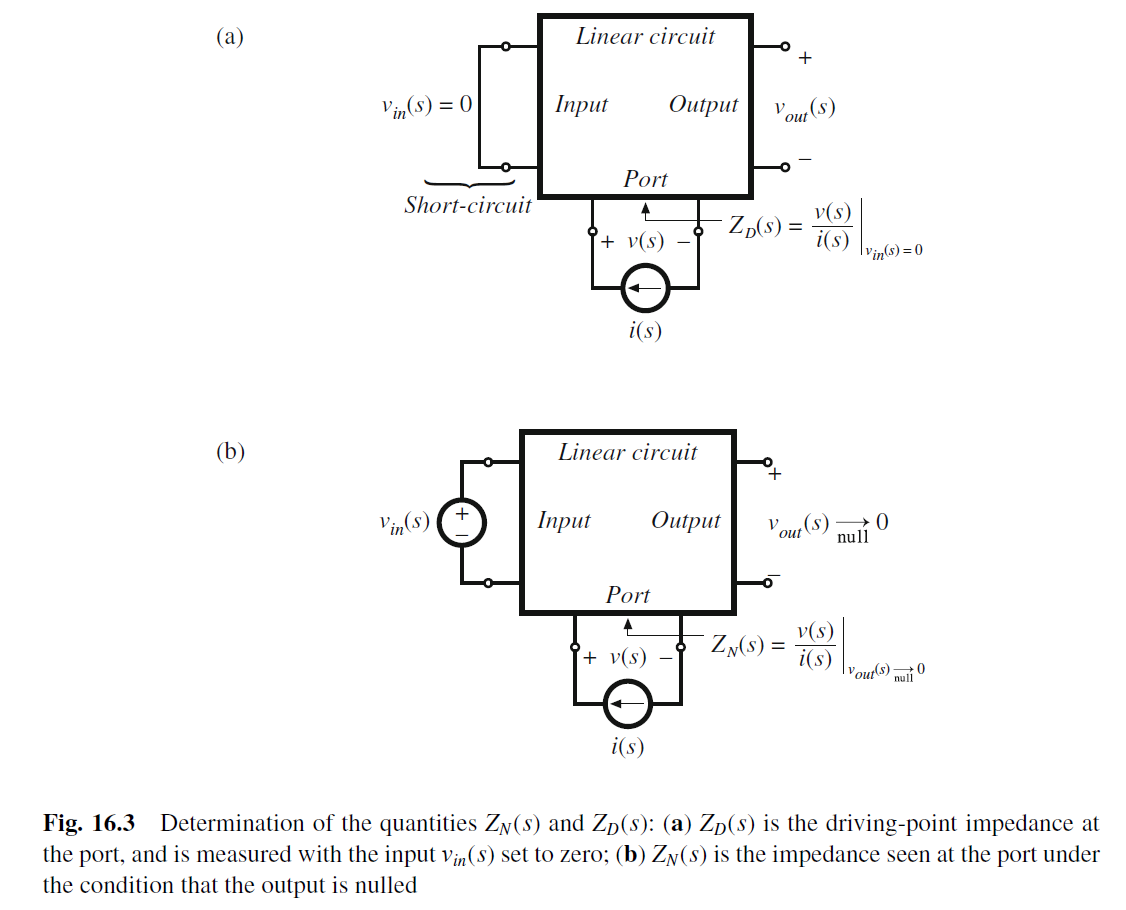
ZD(s): 为从端口看进去的Thevenin equivalent impedance, 即driving-point impedance.
ZD(s): 把vin(s) short to zero后, 从Port看进去的阻抗.
Z D ( s ) = v ( s ) i ( s ) ∣ v i n ( s ) = 0 Z_D(s)=\frac{v(s)}{i(s)}\bigg|_{v_{in}(s)=0} ZD(s)=i(s)v(s) vin(s)=0
ZN(s): 把vout(s) nulled to zero后, 从Port看进去的阻抗.
Z N ( s ) = v ( s ) i ( s ) ∣ v o u t ( s ) → 0 n u l l Z_N(s)=\frac{v(s)}{i(s)}\bigg|_{v_{out}(s)\to 0 null} ZN(s)=i(s)v(s) vout(s)→0null
注意Null不是简单的短路, 是Vout为电压为零, 那么电流也为零, 很多时候ZN的推导更简单.
上面公式的推导省略, 见16.1.2 Derivation
16.2 EET Examples
16.2.1 A Simple Transfer Function
考虑这个RC电路
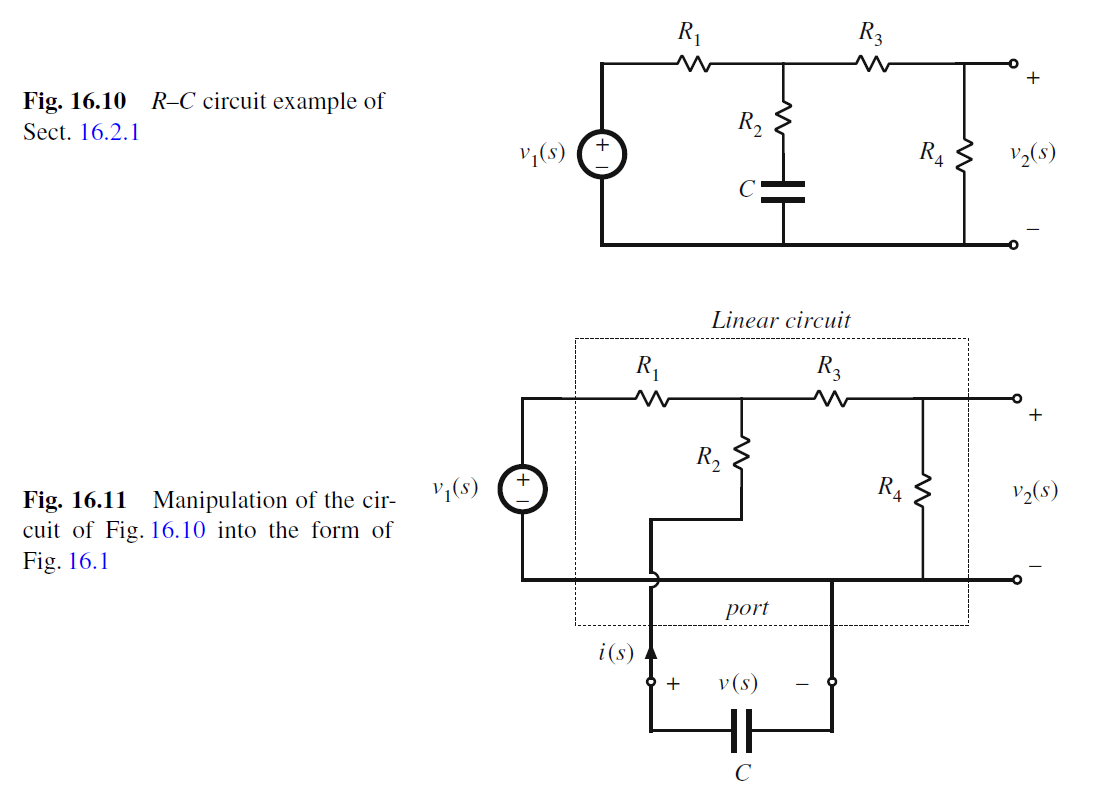
传函V2(s)/V1(s), 把C当成“extra” element, original的传输函数为C两端Port断路, 即C-> inf, R1,R3,R4组成resistor divider.
v 2 ( s ) v 1 ( s ) = G ( s ) = ( R 4 R 1 + R 3 + R 4 ) ( 1 + Z N Z 1 + Z D Z ) \frac{v_{2}(s)}{v_{1}(s)}=G(s)=\left( \frac{R_4}{R_1+R_3+R_4} \right)\left( \frac{1+\frac{Z_{N}}{Z}}{1+\frac{Z_{D}}{Z}} \right) v1(s)v2(s)=G(s)=(R1+R3+R4R4)(1+ZZD1+ZZN)
ZD和ZN求解.
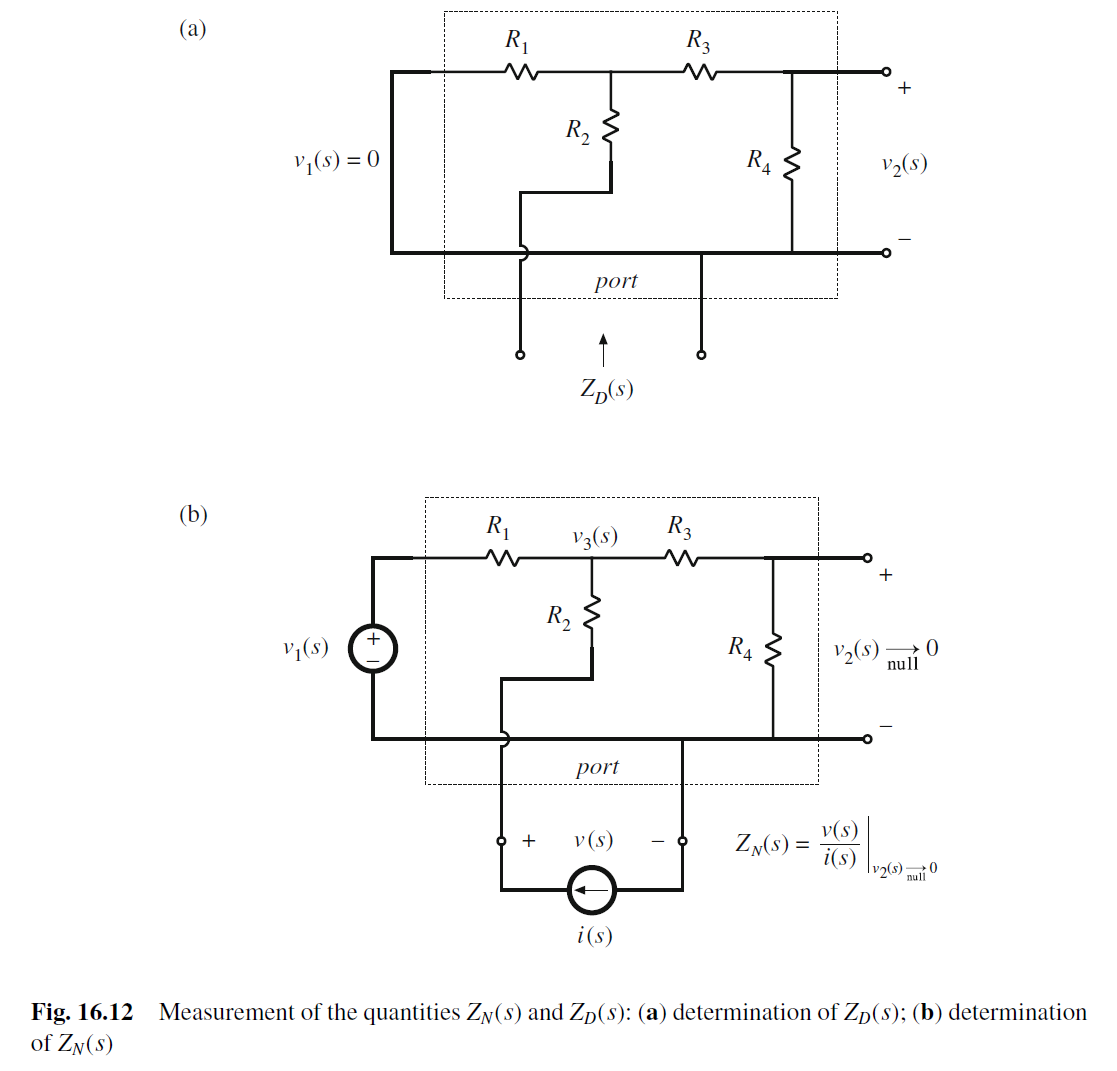
ZD为把输入V1 short后, 从Port ©看进去的阻抗
Z D = R 2 + R 1 ∥ ( R 3 + R 4 ) Z_{D}=R_2+R_1\parallel (R_3+R_4) ZD=R2+R1∥(R3+R4)
ZN为输出V2 nulled to 0, 从Port ©看进去的阻抗.
因为V2 nulled to 0, 因此R4上没有电流, 同理R3上也没有电流, 因此V3 nulled to 0, 因此ZN的impedance为
Z N = v ( s ) i ( s ) ∣ v 2 → n u l l t o 0 = R 2 Z_{N}=\frac{v(s)}{i(s)}\bigg|_{v_{2} \to null to 0}=R_{2} ZN=i(s)v(s) v2→nullto0=R2
Z为电容, Z=1/SC
Z = 1 s C Z=\frac{1}{sC} Z=sC1
因此transfer function G(s)为
G ( s ) = ( R 4 R 1 + R 3 + R 4 ) ( 1 + Z N Z 1 + Z D Z ) = ( R 4 R 1 + R 3 + R 4 ) ( 1 + s C R 2 ) ( 1 + s C [ R 2 + R 1 ∥ ( R 3 + R 4 ) ] ) G(s)=\left( \frac{R_4}{R_1+R_3+R_4} \right)\left( \frac{1+\frac{Z_{N}}{Z}}{1+\frac{Z_{D}}{Z}} \right)=\left( \frac{R_4}{R_1+R_3+R_4} \right)\frac{(1+sCR_{2})}{(1+sC[R_2+R_1\parallel (R_3+R_4)])} G(s)=(R1+R3+R4R4)(1+ZZD1+ZZN)=(R1+R3+R4R4)(1+sC[R2+R1∥(R3+R4)])(1+sCR2)
16.2.2 An Unmodeled Element
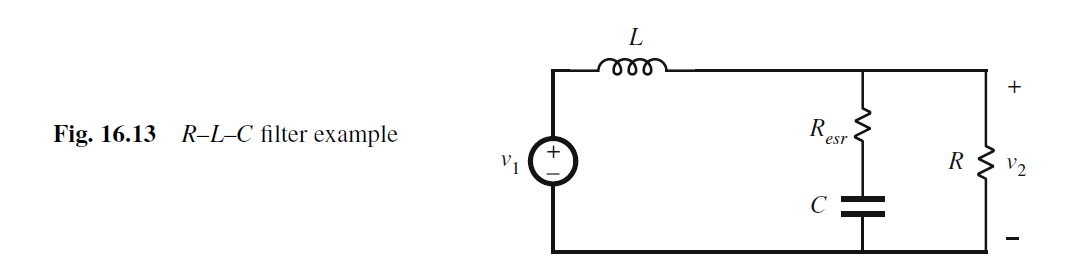
考虑电容的equivalent series resistance (ESR), 推导传输函数G=v2/v1
没有ESR下, 传输函数为
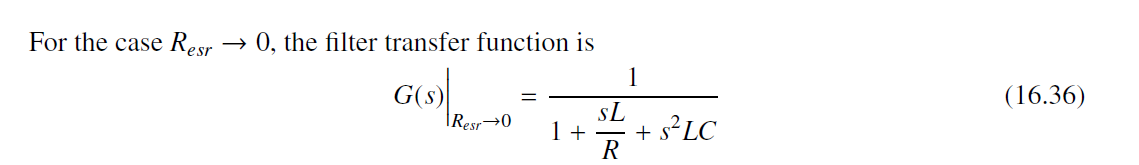
考虑ESR, 传输函数为
G ( s ) = ( G ( s ) ∣ R e s r → 0 ) ( 1 + Z ( s ) Z N ( s ) 1 + Z ( s ) Z D ( s ) ) G(s)=\left( G(s)\bigg|_{R_{esr}\to 0} \right)\left( \frac{1+\frac{Z(s)}{Z_{N}(s)}}{1+\frac{Z(s)}{Z_{D}(s)}} \right) G(s)=(G(s) Resr→0) 1+ZD(s)Z(s)1+ZN(s)Z(s)
ZD和ZN的推导
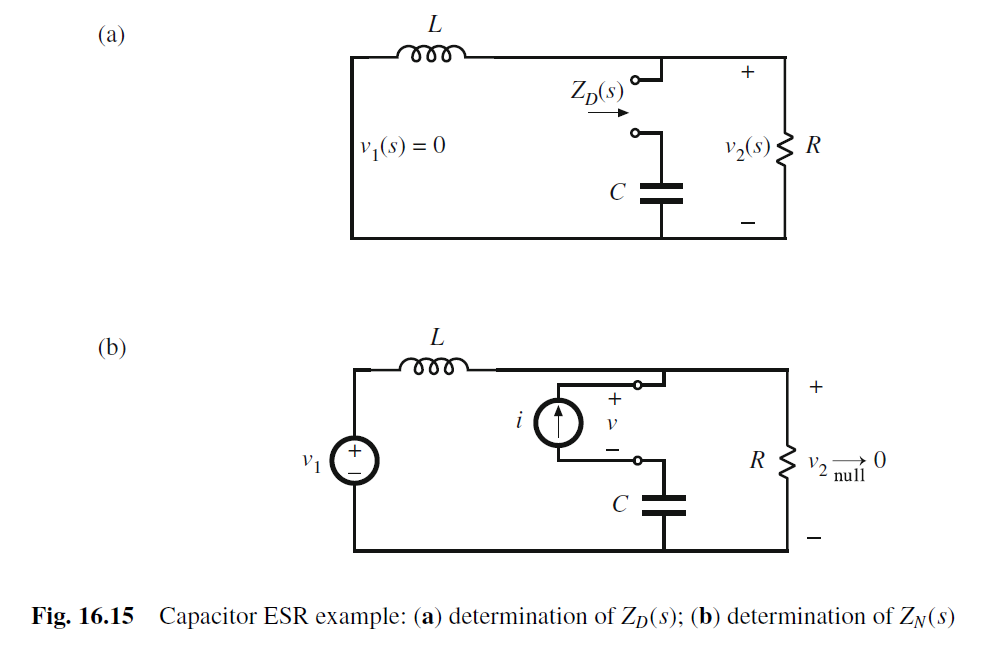
ZD为把输入V1 short后, 从Port ®看进去的阻抗, 即C串联 (L并联R)
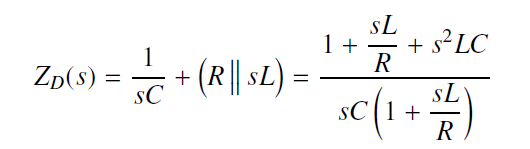
ZN为输出V2 nulled to 0, 从Port ®看进去的阻抗, 即C
Z N = 1 s C Z_{N}=\frac{1}{sC} ZN=sC1
Z为ESR电阻, Z=Resr.
因此传输函数为
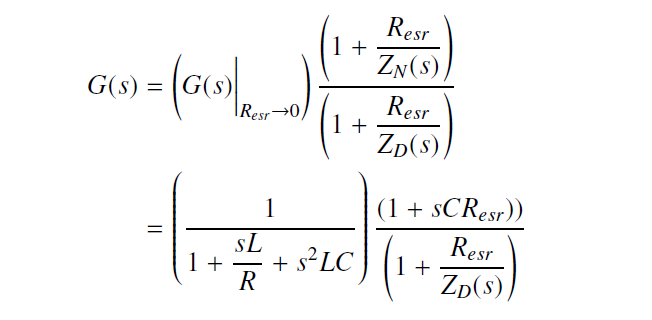
可以看到ESR引入的correction factor 有了一个零点 W=1/(Resr*C). 当Resr << ZD, 引入的极点可忽略不计 .
Resr的bode plot如下. 在f0处ZD最接近Resr. ZD=1, 分母为3.
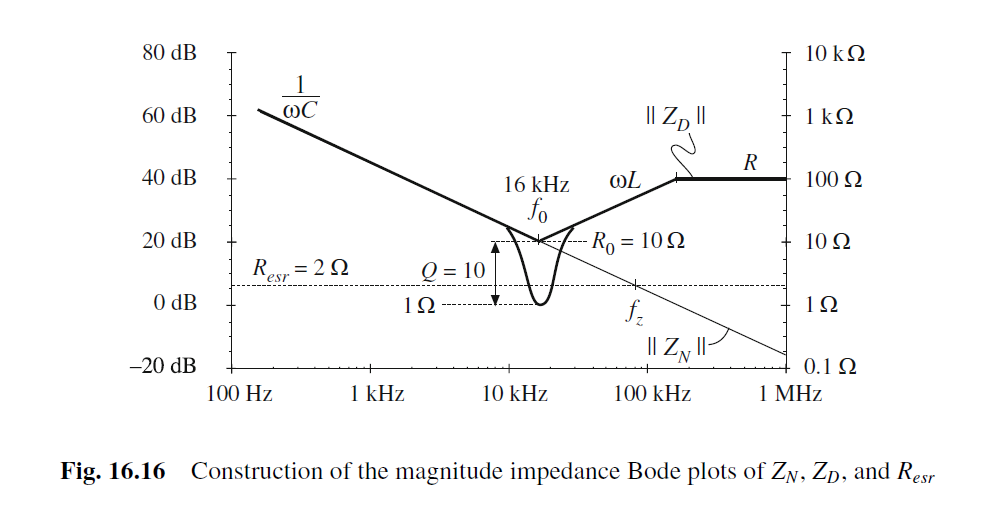
因此考虑电容ESR的Transfer Function为

16.2.3 SEPIC Example
SEPIC小信号模型如下
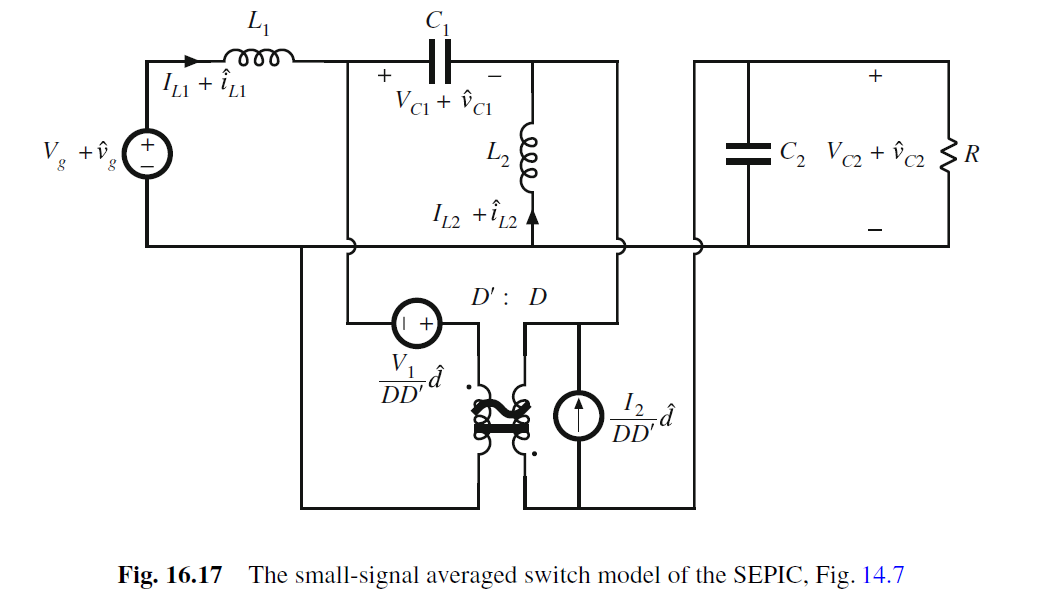
考虑把C1断路简化电路, SEPIC就成buck-boost converter
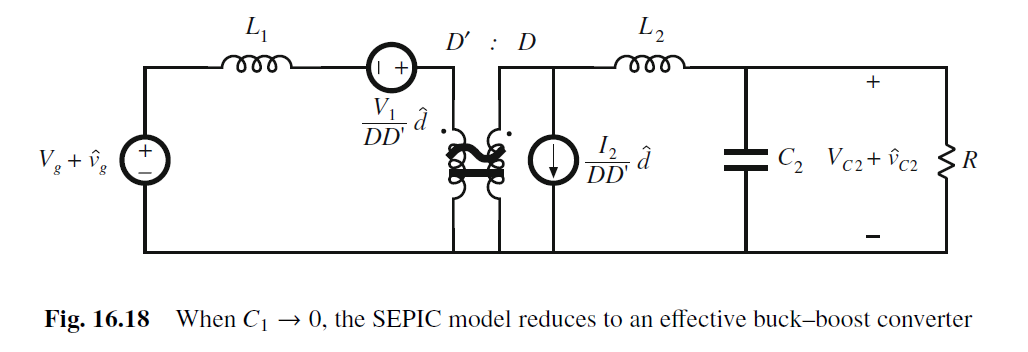
buck-boost的传输函数为
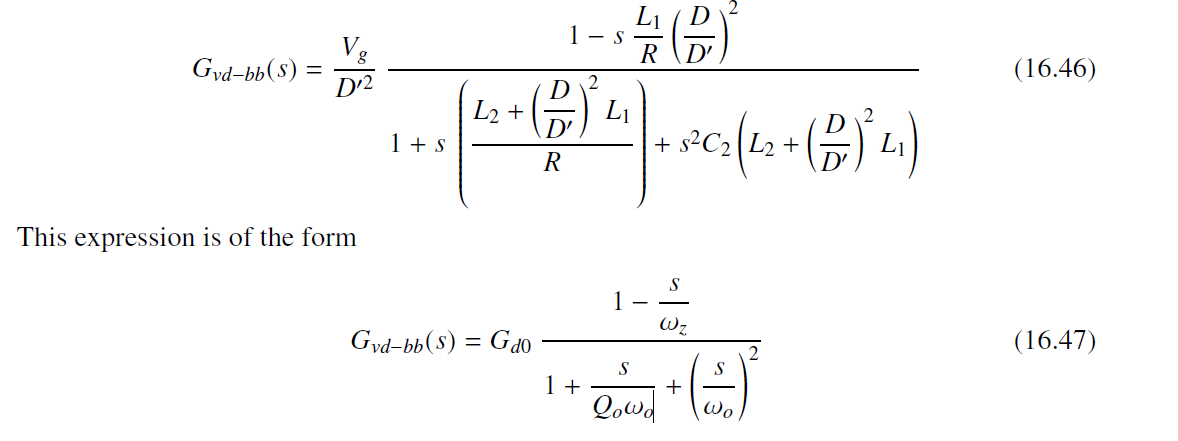
SEPIC bole plot vs Buck-Boost Bode Plot:
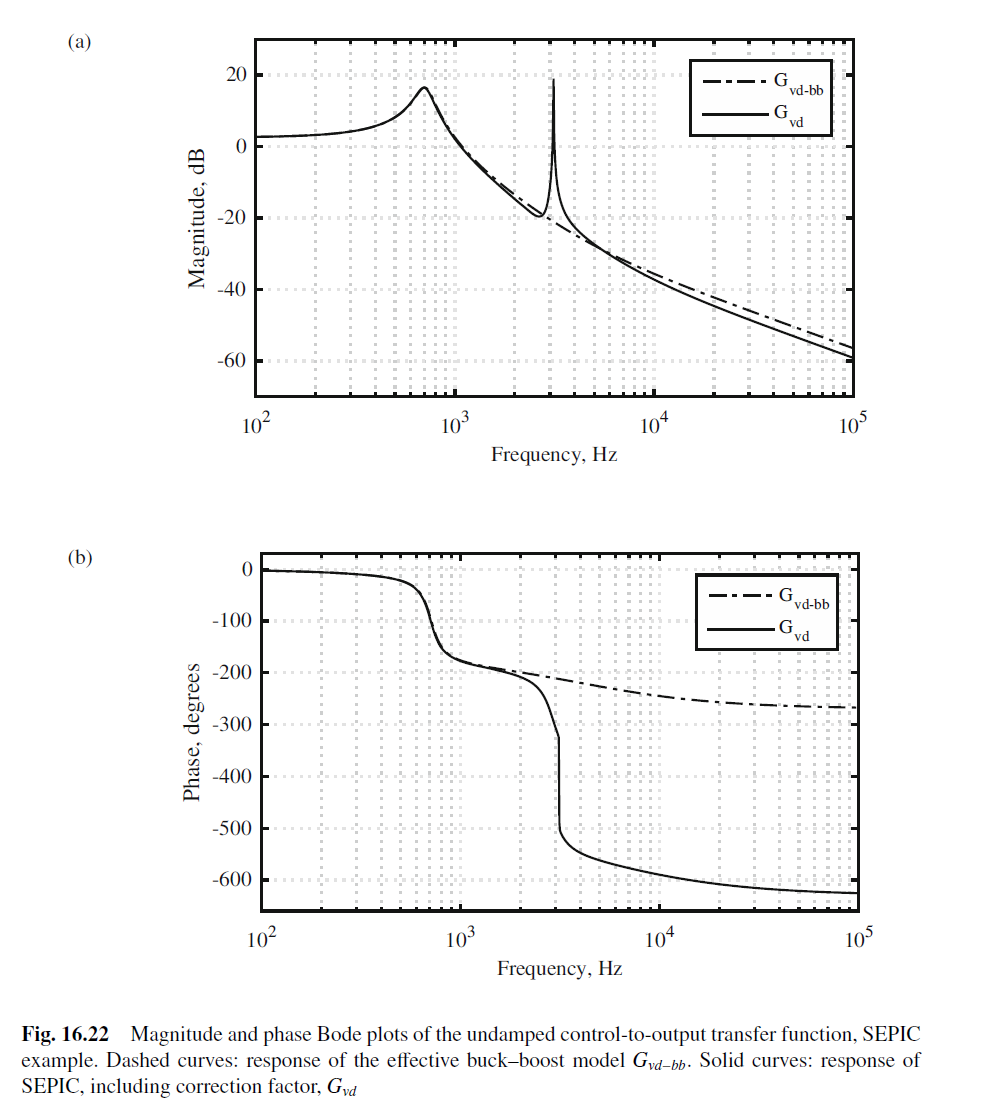
可以考虑在SEPIC的C1上加入Cb和Rb damping network.
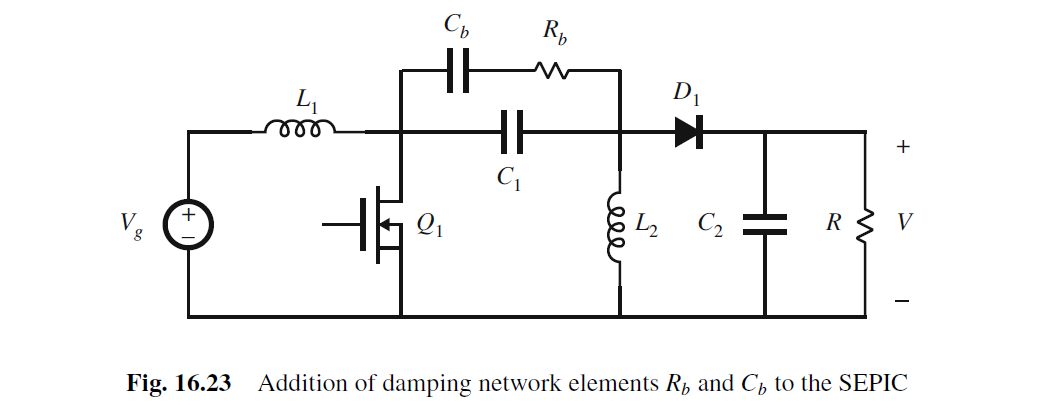
这样extra element 的impedance Z= (1/SC) || [Rb+1/(SCb)]
当Z接近ZN和ZD的频率时, 让Z=Rb.
The damping network reduces the Q–factors of the poles and zeroes of the correction factor, and can also move its RHP zeroes into the left half-plane.
加入Rb可以让右零点移到左半平面零点. 加入Cb做DC voltage blocking, 防止Rb上有DC电流流过.
16.3 The n-Extra Element Theorem
n Extra Element Theorem (nEET) 是 Extra Element Theorem的拓展, 把电感和电容看成“extra” elements. 这样可以直接写出分子分母式的传输函数, 而不用节点分析和数学推导.
定义两个概念:
DC state: 在DC态下, 电感短路, 电容断路.
HF state: 在高频态下, 电感开路, 电容短路.
包含LC的传输函数就是低频态+高频态的纠正项. 在求分母时, 输入信号Vin is shorted to zero. 在求分子时, 输出Vout is nulled.
以下面这个带ESR的LC电路为例
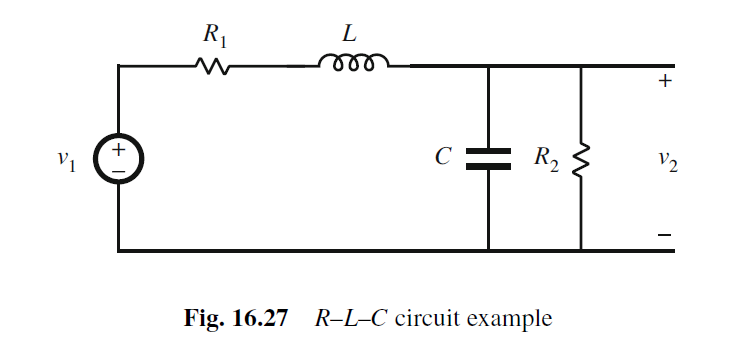
传输函数应该为
G ( s ) = G d c 1 1 + b 1 s + b 2 s 2 G(s)=G_{dc}\frac{1}{1+b_{1}s+b_{2}s^{2}} G(s)=Gdc1+b1s+b2s21
b1的单位为Hz^-1, 因此b1的形式应该为L/Ra和Rb*C
b2的单位为Hz^-2, 因此b2的形式应该为L/Rc*Rd *C
Gdc很容易得到:
G d c = R 2 R 1 + R 2 G_{dc}=\frac{R_{2}}{R_{1}+R_{2}} Gdc=R1+R2R2
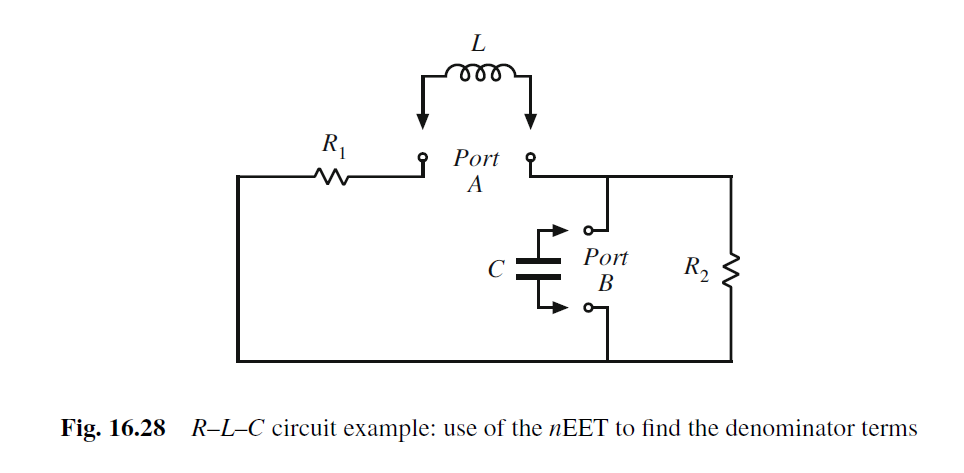
分母denominator写成这样形式
denominator = 1 + s ( L R a + R b C ) + s 2 ( L R c R d C ) \text{denominator}=1+s(\frac{L}{R_{a}}+R_{b}C)+s^{2}(\frac{L}{R_{c}}R_{d}C) denominator=1+s(RaL+RbC)+s2(RcLRdC)
s^1的系数:
Ra是从Port A即inductor看进去阻抗, 同时电容在DC state (断路).
Ra=R1+R2
Rb是从Port B即capacitor看进去阻抗, 同时电感在DC state (短路).
Rb=R1||R2
对于s^2的系数, Rc和Rd我们可以选择其中一个等同于s^1的系数
Rc=Ra=R1+R2
Rd是从Port B即capacitor看进去阻抗, 同时电感在HF state (开路).
Rd=R2
因此可得传输函数
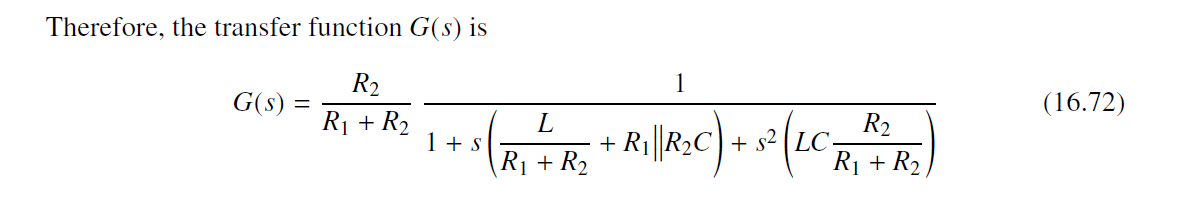
16.4 n-EET Examples
16.4.1 Two-Section L–C Filter
我们以两级L-C filter为例
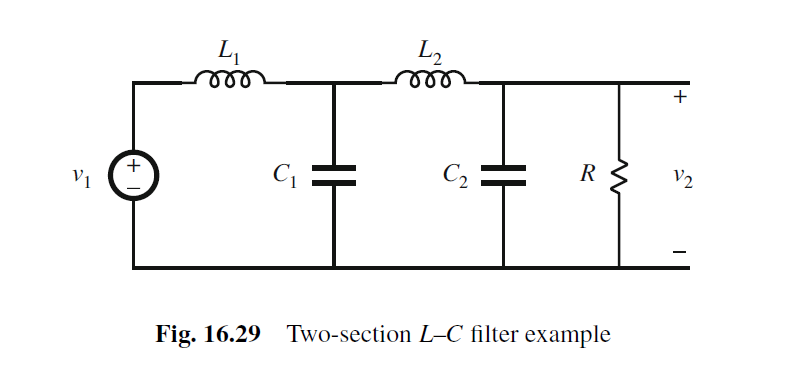
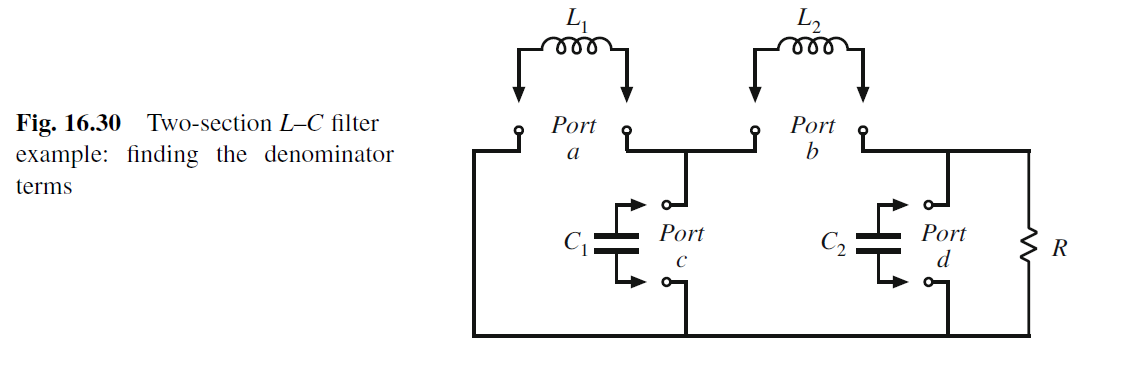
推导各项系数如下:
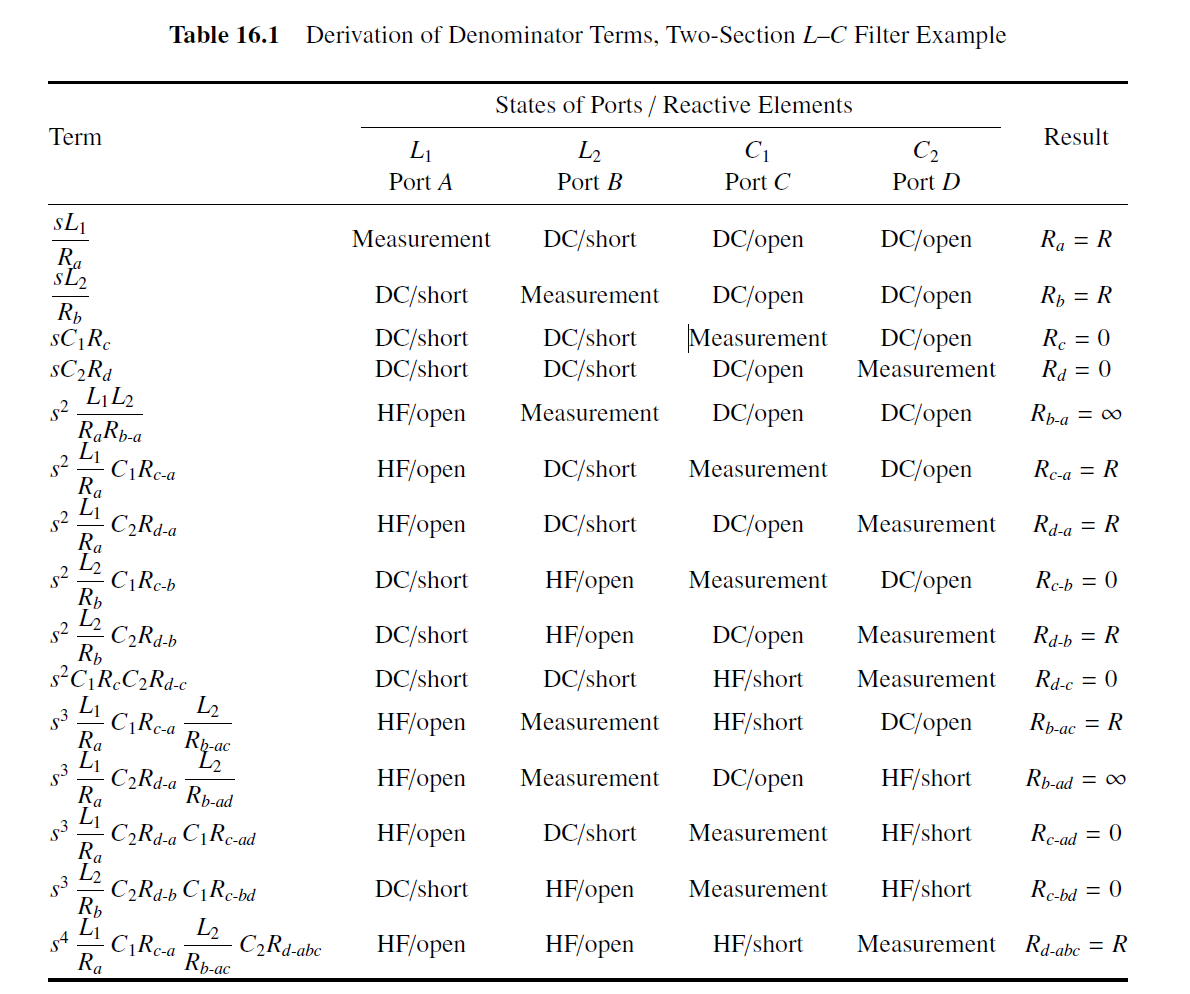
最终我们得到传输函数:
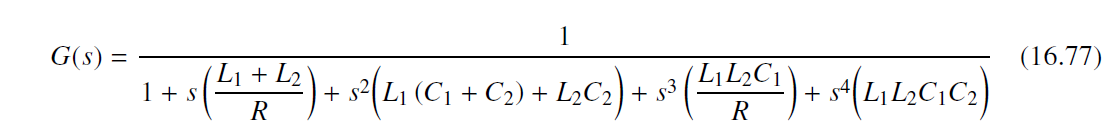
16.4.2 Bridge-T Filter Example
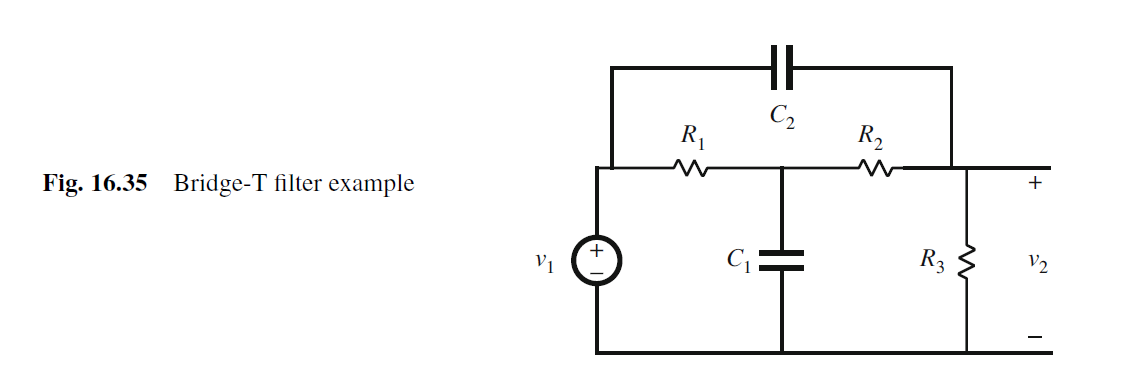
因为有两个电容, 因此传输函数G有两个极点. 又因为在高频时Gain为1 (C2 short), 因此传输函数有两个零点.
因此传输函数可以写成这样的形式:
G ( s ) = G d c 1 + a 1 s + a 2 s 2 1 + b 1 s + b 2 s 2 G(s)=G_{dc}\frac{1+a_{1}s+a_{2}s^{2}}{1+b_{1}s+b_{2}s^{2}} G(s)=Gdc1+b1s+b2s21+a1s+a2s2
其中分子的形式:
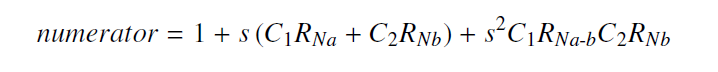
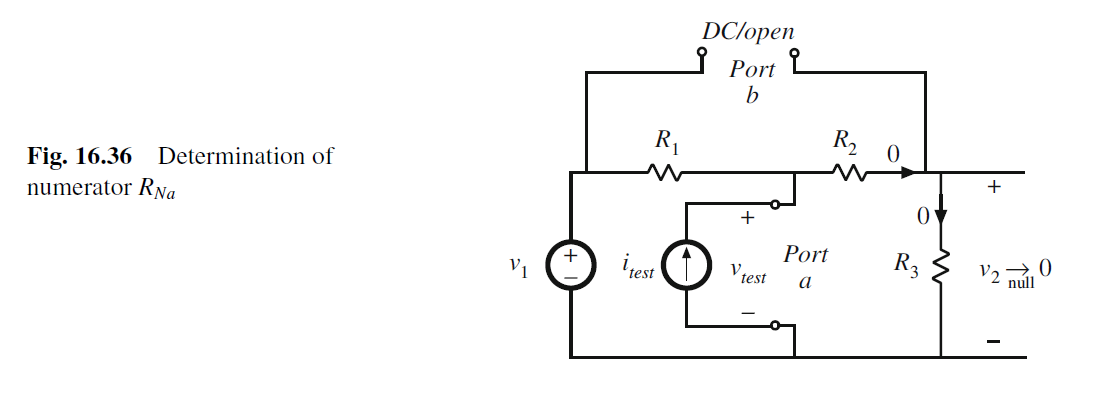
在求分子时, 输出v2 is nulled to zero.
求RNa时, PortB Open, V2 nulled, 因此 RNa=0
求RNb时, PortA Open, V2 nulled, 因此 RNb=R1+R2
求RNab时, 测量PortA, PortB in HF state, 即PortB short, V2 nulled, 因此 RNa-b=R1||R2.
在求分母时, 输入v1 is shorted to zero.
求RDa时, PortB Open, V1 shorted, 因此 RDa=R1||(R2+R3)
求RDb时, PortA Open, V1 shorted, 因此 RDb=R3||(R1+R2)
求RDab时, 测量PortA, PortB in HF state, 即PortB short, V1 shorted, 因此 RDa-b=R1||R2.
最后可得DC Gain
Gdc=R3/(R1+R2+R3)
16.5 Frequency Inversion
在电力电子中, 我们总不希望DC或者low-frequency ac电流流过lossy电阻. 这常用于补偿网路, 例如PI或者PID.
例如下图的damping LC filter network
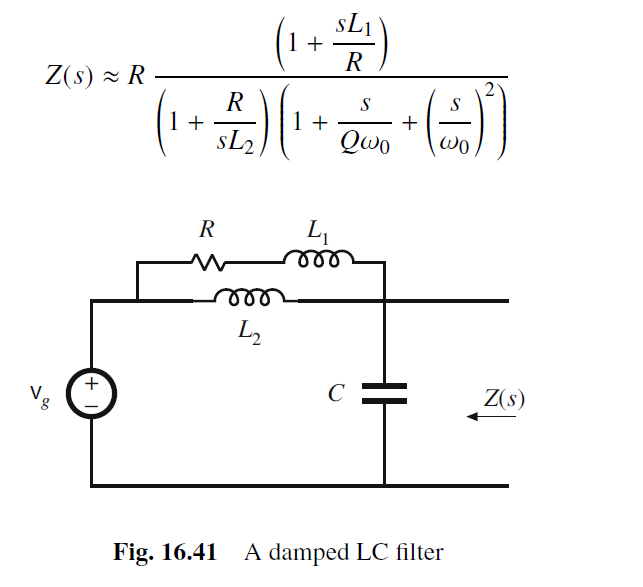

我们不能简单的用DC state和HF state 推导传输函数. 可以用Reference state和Inverse state:
16.5.2 Other Special Cases
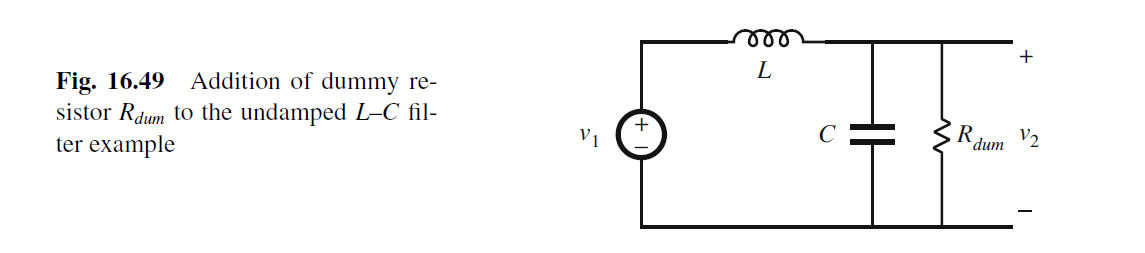
对于Undamped L–C filter, 因为s^1的系数=0, 我们得不到s^2的系数 (0*inf)
解决办法可以加入Rdummy, 然后让Rdummy->infinity, 这样就能推导出传输函数了.
这篇关于Chapter 16 Techniques of Design-Oriented Analysis: Extra Element Theorems的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!