本文主要是介绍如何通俗理解 beta分布、汤普森采样和狄利克雷分布,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
如果想理解汤普森采样算法,就必须先熟悉了解贝塔分布。
一次伯努利实验(比如扔硬币,二元变量)叫做伯努利分布(Bernoulli distribution)。多次伯努利实验叫做二项式分布(Binomial distribution,还是二元变量),加个先验就是beta分布。
二项式分布变成多元就成了多项式分布(multinomial distribution),beta分布搞到多元就是Dirichlet分布。
Dirichlet分布是Beta分布的多元推广。Beta分布是二项式分布的共轭分布,Dirichlet分布是多项式分布的共轭分布。通常情况下,我们说的分布都是关于某个参数的函数,把对应的参数换成一个函数(函数也可以理解成某分布的概率密度)就变成了关于函数的函数。于是,把Dirichlet分布里面的参数换成一个基分布就变成了一个关于分布的分布了。那么它就是Dirichlet过程了。可以参考如下资料:
Dirichlet Distribution(狄利克雷分布)与Dirichlet Process(狄利克雷过程) | 学习数据 | 数据学习者官方网站
一、Beta(贝塔)分布
Beta分布是一个定义在[0,1]区间上的连续概率分布族,它有两个正值参数,称为形状参数,一般用α和β表示,Beta分布的概率密度函数形式如下:
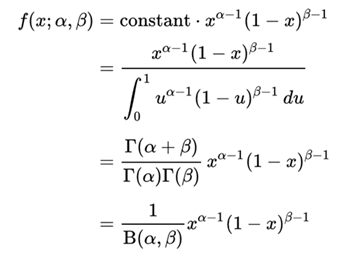
这里的Γ表示gamma函数。
Beta分布的均值是:
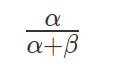
方差:
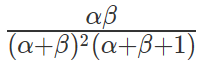
Beta分布的图形(概率密度函数):
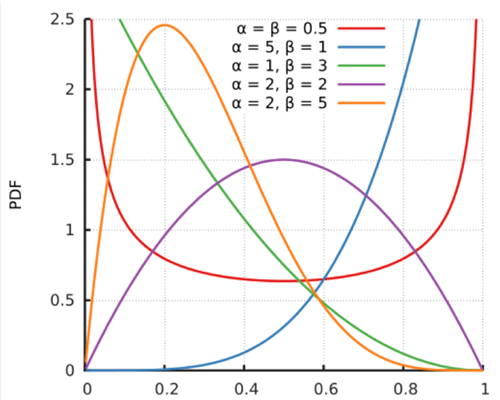
从Beta分布的概率密度函数的图形我们可以看出,Beta分布有很多种形状,但都是在0-1区间内,因此Beta分布可以描述各种0-1区间内的形状(事件)。因此,它特别适合为某件事发生或者成功的概率建模。同时,当α=1,β=1的时候,它就是一个均匀分布。
贝塔分布主要有 α和 β两个参数,这两个参数决定了分布的形状,从上图及其均值和方差的公式可以看出:
1)α/(α+β)也就是均值,其越大,概率密度分布的中心位置越靠近1,依据此概率分布产生的随机数也多说都靠近1,反之则都靠近0。
2)α+β越大,则分布越窄,也就是集中度越高,这样产生的随机数更接近中心位置,从方差公式上也能看出来。
二、举例理解Beta分布
贝塔分布可以看作是一个概率的分布,当我们不知道一个东西的具体概率是多少时,它给出了所有概率出现的可能性大小,可以理解为概率的概率分布。
以棒球为例子:
棒球运动的一个指标就是棒球击球率,就是用一个运动员击中的球数除以总的击球数,一般认为0.27是一个平均的击球水平,如果击球率达到0.3就会认为非常优秀了。如果我们要预测一个棒球运动员,他整个赛季的棒球击球率,怎么做呢?你可以直接计算他目前的棒球击球率,用击中数除以击球数。但是,这在赛季开始阶段时是很不合理的。假如这个运动员就打了一次,还中了,那么他的击球率就是100%;如果没中,那么就是0%,甚至打5、6次的时候,也可能运气爆棚全中击球率100%,或者运气很糟击球率0%,所以这样计算出来的击球率是不合理也是不准确的。
为什么呢?
当运动员首次击球没中时,没人认为他整个赛季都会一次不中,所以击球率不可能为0。因为我们有先验期望,根据历史信息,我们知道击球率一般会在0.215到0.36之间。如果一个运动员一开始打了几次没中,那么我们知道他可能最终成绩会比平均稍微差一点,但是一般不可能会偏离上述区间,更不可能为0。
如何解决呢?
一个最好的方法来表示这些先验期望(统计中称为先验(prior))就是贝塔分布,表示在运动员打球之前,我们就对他的击球率有了一个大概范围的预测。假设我们预计运动员整个赛季的击球率平均值大概是0.27左右,范围大概是在0.21到0.35之间。那么用贝塔分布来表示,我们可以取参数 α=81,β=219,因为α/(α+β)=0.27,图形分布也主要集中在0.21~0.35之间,非常符合经验值,也就是我们在不知道这个运动员真正击球水平的情况下,我们先给一个平均的击球率的分布。
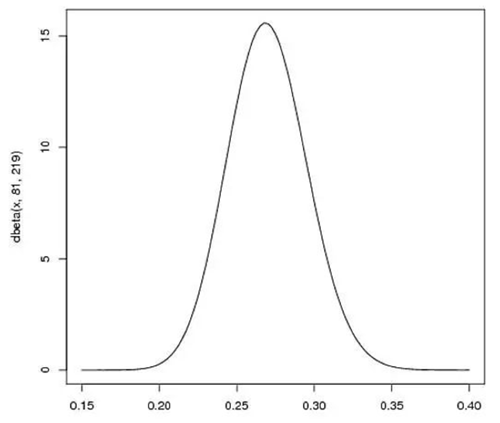
假设运动员一次击中,那么现在他本赛季的记录是“1次打中;1次打击”。那么我们更新我们的概率分布,让概率曲线做一些移动来反应我们的新信息。
Beta(α0+hits,β0+misses)
注:α0,β0是初始化参数,也就是本例中的81,219。hits表示击中的次数,misses表示未击中的次数。
击中一次,则新的贝塔分布为Beta(81+1,219),一次并不能反映太大问题,所以在图形上变化也不大,不画示意图了。然而,随着整个赛季运动员逐渐进行比赛,这个曲线也会逐渐移动以匹配最新的数据。由于我们拥有了更多的数据,因此曲线(击球率范围)会逐渐变窄。假设赛季过半时,运动员一共打了300次,其中击中100次。那么新的贝塔分布是Beta(81+100,219+200),如下图:
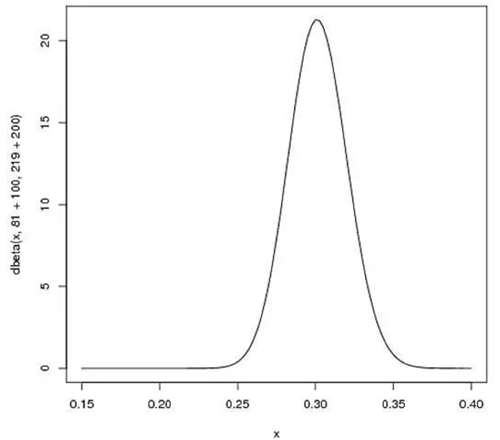
可以看出,曲线更窄而且往右移动了(击球率更高),由此我们对于运动员的击球率有了更好的了解。新的贝塔分布的期望值为0.303,比直接计算100/(100+200)=0.333要低,是比赛季开始时的预计0.27要高,所以贝塔分布能够抛出掉一些偶然因素,比直接计算击球率更能客观反映球员的击球水平。
总结:
这个公式就相当于给运动员的击中次数添加了“初始值”,相当于在赛季开始前,运动员已经有81次击中219次不中的记录。 因此,在我们事先不知道概率是什么但又有一些合理的猜测时,贝塔分布能够很好地表示为一个概率的分布。
三、汤普森采样
汤普森采样的背后原理正是上述所讲的Beta分布,你把贝塔分布的 a 参数看成是推荐后用户点击的次数,把分布的 b 参数看成是推荐后用户未点击的次数,则汤普森采样过程如下:
1、取出每一个候选对应的参数 a 和 b;
2、为每个候选用 a 和 b 作为参数,用贝塔分布产生一个随机数;
3、按照随机数排序,输出最大值对应的候选;
4、观察用户反馈,如果用户点击则将对应候选的 a 加 1,否则 b 加 1;
注:实际上在推荐系统中,要为每一个用户都保存一套参数,比如候选有 m 个,用户有 n 个,那么就要保存 2 m n个参数。
汤普森采样为什么有效呢?
1)如果一个候选被选中的次数很多,也就是 a+b 很大了,它的分布会很窄,换句话说这个候选的收益已经非常确定了,就是说不管分布中心接近0还是1都几乎比较确定了。用它产生随机数,基本上就在中心位置附近,接近平均收益。
2)如果一个候选不但 a+b 很大,即分布很窄,而且 a/(a+b) 也很大,接近 1,那就确定这是个好的候选项,平均收益很好,每次选择很占优势,就进入利用阶段。反之则有可能平均分布比较接近与0,几乎再无出头之日。
3)如果一个候选的 a+b 很小,分布很宽,也就是没有被选择太多次,说明这个候选是好是坏还不太确定,那么分布就是跳跃的,这次可能好,下次就可能坏,也就是还有机会存在,没有完全抛弃。那么用它产生随机数就有可能得到一个较大的随机数,在排序时被优先输出,这就起到了前面说的探索作用。
python代码实现:
choice = numpy.argmax(pymc.rbeta(1 + self.wins, 1 + self.trials - self.wins))
这篇关于如何通俗理解 beta分布、汤普森采样和狄利克雷分布的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






