狄利克专题
【Python机器学习】NLP词频背后的含义——隐性狄利克雷分布(LDiA)
目录 LDiA思想 基于LDiA主题模型的短消息语义分析 LDiA+LDA=垃圾消息过滤器 更公平的对比:32个LDiA主题 对于大多数主题建模、语义搜索或基于内容的推荐引擎来说,LSA应该是首选方法。它的数学机理直观、有效,它会产生一个线性变换,可以应用于新来的自然语言文本而不需要训练过程,并几乎不会损失精确率。但是,在某些情况下,LDiA可以给出稍好的结果。 LDiA和LS
基于狄利克雷DirichletProcesses聚类的协同过滤推荐算法代码实现(输出聚类计算过程,分布图展示)
基于狄利克雷DirichletProcesses聚类的协同过滤推荐算法代码实现(输出聚类计算过程,分布图展示) 聚类(Clustering)就是将数据对象分组成为多个类或者簇 (Cluster),它的目标是:在同一个簇中的对象之间具有较高的相似度,而不同簇中的对象差别较大。所以,在很多应用中,一个簇中的数据对象可以被作为一个整体来对待,从而减少计算量或者提高计算质量。 一、DirichletP
20、matlab信号波形生成:狄利克雷函数、高斯脉冲和高斯脉冲序列
1、狄利克雷函数生成波形diric()函数 语法:y = diric(x,n) 返回n次的狄利克雷函数对输入数组x的元素求值。 1)diric()函数 代码 x = linspace(-2*pi,2*pi,301);%定义x取值d6 = diric(x,6);d7 = diric(x,7);subplot(2,1,1)plot(x,d6)ylabel('n= 6')title(
漫步数学分析二十八——狄利克雷与阿贝尔测试
在我们判断一致收敛的时候,某些情况下魏尔斯特拉斯M测试会失效,为此挪威数学家尼尔斯阿贝尔(Niels Abel)以及狄利克雷(Dirichlet)分别提出了两种测试方法,这些方法对许多实例都是非常有用的,尤其是研究傅里叶与幂级数的时候,当我们碰到一致收敛却不是绝对收敛的时候,这些方法非常重要。 定理13 \textbf{定理13}(阿贝尔测试) 令 A⊂Rm,φn:A→R A\subset R
狄利克雷卷积 【HDU5628】Clarke and math
题目大意: 给定f(1~n),求g(1~n) 题目分析:(狄利克雷卷积) 狄利克雷卷积: 狄利克雷卷积满足:交换律,结合律,分配率等性质(和乘法是一样的)。 我们设函数g(i)=1 如果k==1,则 i 的答案为: (f∗g)(n)=∑d1|nf(d1) ( f ∗ g ) ( n ) = ∑ d 1 | n f ( d 1 ) (f*g)(n)=\sum_{d_1|n}{f
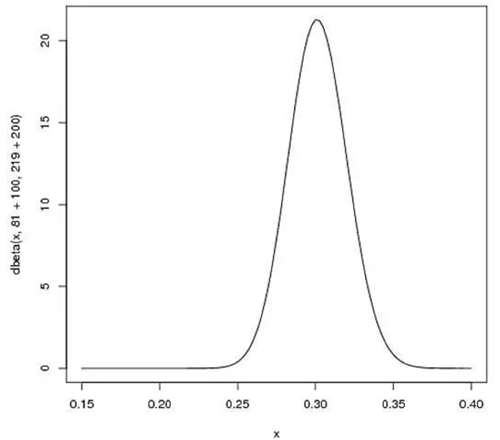
如何通俗理解 beta分布、汤普森采样和狄利克雷分布
如果想理解汤普森采样算法,就必须先熟悉了解贝塔分布。 一次伯努利实验(比如扔硬币,二元变量)叫做伯努利分布(Bernoulli distribution)。多次伯努利实验叫做二项式分布(Binomial distribution,还是二元变量),加个先验就是beta分布。 二项式分布变成多元就成了多项式分布(multinomial distribution),beta分布搞到多元就是Diri
《微积分:一元函数微分学》——狄利克雷函数
定义 性质 狄利克雷函数是一个有界的偶函数,且任何有理数都是它的周期,它没有最小的周期 应用 函数 f(x) 在点 x=x0 可导,那么 f(x) 在点 x=x0 处必然连续,如果函数 f(x) 在点 x=x0 处可导,并不一定存在点 x=x0 的某个邻域,使得函数在这个邻域内连续 使用狄利克雷函数构造一个反例 根据 ”无穷小量乘有界函数仍然是无穷小量“ 可知上述结果
【机器学习前置知识】狄利克雷分布
在阅读本文前,建议先食用以下几篇文章以能更好地理解狄利克雷分布: 二项分布 Beta分布 多项分布 共轭分布 狄利克雷分布 狄利克雷分布(Dirichlet distribution)是Beta分布的扩展,把Beta分布从二元扩展到多元形式就是狄利克雷分布,Beta分布是狄利克雷分布的二元特例。 在共轭方面,可以类比Beta分布与二项分布的关系,狄利克雷分布是多项分布的共轭分布,因此
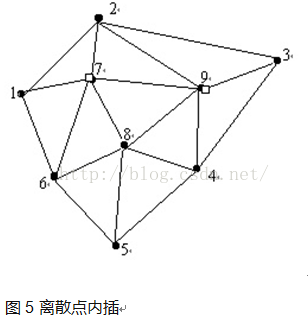
沃罗诺伊图(Voronoi Diagram,也称作Dirichlet tessellation,狄利克雷镶嵌)
沃罗诺伊图(Voronoi Diagram,也称作Dirichlet tessellation,狄利克雷镶嵌)是由俄国数学家格奥尔吉·沃罗诺伊建立的空间分割算法。灵感来源于笛卡尔用凸域分割空间的思想。在几何,晶体学建筑学,地理学,气象学,信息系统等许多领域有广泛的应用。 泰森多边形法,荷兰气候学家A·H·Thiessen提出了一种根据离散分布的气象站的降雨量,来计算平均降雨量的方法,即将所有相邻
【bzoj4407】于神之怒加强版 莫比乌斯反演+狄利克雷卷积
Description 给下N,M,K.求 Input 输入有多组数据,输入数据的第一行两个正整数T,K,代表有T组数据,K的意义如上所示,下面第二行到第T+1行,每行为两个正整数N,M,其意义如上式所示。 Output 如题 Sample Input 1 2 3 3 Sample Output 20 HINT 1<=N,M,K<=5000000,1<=T<=2000