本文主要是介绍关于 相似的数集 的思路+时间复杂度分析+代码,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
最优解法可以直接参考这位学长的文章
题目来源:NEFU OJ-2119 相似的数集简单版
以及NEFU OJ-???? 相似的数集高级版
后者链接已补。
主要区别在高级版数据范围和数据量均大于前者,接下来将以高级版为主。
题目描述
给出两个数集,它们的相似程度定义为Nc/Nt*100%。其中,Nc表示两个数集中相等的、两两互不相同的元素个数,而Nt表示两个数集中总共的互不相同的元素个数。请计算任意两个给出数集的相似程度。
输入描述
输入第一行给出一个正整数N(N<=50),是集合的个数。随后N行,每行对应一个集合。每个集合首先给出一个正整数M(M<=104),是集合中元素的个数;然后跟M个[0, 109]区间内的整数。
之后一行给出一个正整数K(K<=2000),随后K行,每行对应一对需要计算相似度的集合的编号(集合从1到N编号)。数字间以空格分隔。
第二行给出N个数字,第i个数字表示第i道题通过的人数ai (0≤ai≤M)。输出描述
输出共K行,每行一个保留2位小数的实数,表示给定两个集合的相似度值。
输入样例
3
3 99 87 101
4 87 101 5 87
7 99 101 18 5 135 18 99
2
1 2
1 3输出样例
50.00%
33.33%
OP
本题大体思路不复杂,主要在如何降低时间复杂度上。
思路
就题干来说,Nc为被询问的两个集合中重复元素的对数,Nt为两个集合中有多少个不同的数。
用数学语言来说,Nc为被询问的两个集合的交集元素个数,Nt为并集元素个数。
所以我们的目标很明确:1.去重;2.交集计数,经测试,oj的测试组中含有重复询问组,所以还有 3.记忆化。
对于去重,我们可以用set / 数组+unique / 桶排。
对于计数,我们可以双指针计重 / 求交集函数 / map模拟桶排查找键值
去重
set
set性质,不多说;
数组+unique
数组接收后,sort排序,再用unique函数完全去重;
桶排
对于109的数量级,开数组是不现实的(简单版范围较小,可以使用),便想用unordered_map模拟桶排(此路后面会被毙)。
交集计数
下面的时间复杂度都是对于单次询问的,m,n分别为两个数集的长度
PLAN A
来自学长和lpc大佬。
时间复杂度O(min(m , n))
双指针在排序后的数组中实现交集计数
while(sp1<arr[s1-1][10000]&&sp2<arr[s2-1][10000]) {//小的元素指针+1,元素相等same+1if(arr[s1-1][sp1]<arr[s2-1][sp2])sp1++;else if(arr[s1-1][sp1]>arr[s2-1][sp2])sp2++;else{same++;sp1++;sp2++;}}
这种方法不加记忆化处理也能在时间限制内横着走。
注:经ph大佬测试,在set中使用迭代器实现这种方法同样会超时,原因目前认为是容器问题。推测map模拟桶排使用这种方法也会超时。
PLAN B
来自ph大佬
时间复杂度O(m+n)
使用取交集函数(也可以参考这篇文章)。
set_intersection(l[p].begin(),l[p].end(),l[q].begin(),l[q].end(),inserter(s,s.begin()));int cou = s.size();
注:使用取交集函数时,可以如下图,方便一些
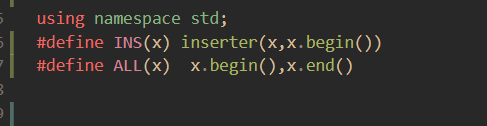

注2:这种方法时间限制压的很死,需要搭配记忆化才能避免TLE。
PLAN C
时间复杂度O(m * log n)
通过预处理也只能优化到O( min(m , n) * log( max(m , n)))
妥妥TLE,map的.find()函数时间复杂度是O(log n),unorder_map也救不了。(经测试,2119中,unordered_map/252ms/会比map/472ms/快一倍)(2119中,数组桶排则可以压缩至/43ms/)
数据来源:这里和这里。
//要定义迭代器itfor(it=s[p].begin(); it!=s[p].end(); it++)if(s[q].find(it->first)!=s[q].end())//找到即数集q中含有it->first{cou++;}
使用这种方法时,如果像下片写代码,会存在引用不存在键值的情况,将出现一些问题,详细描述及解决方法可以参照这篇文章。
for(it=s[p].begin();it!=s[p].end();it++)if(s[q][it->first])cou++;
即某些在p数集中存在的键值在q中不存在,但在q中被引用。
注:下片的时间复杂度或许小一些?
代码
①数组+unique去重,双指针交集计数;/2119-72ms/
#include <bits/stdc++.h>
using namespace std;int main()
{int arr[50][10001]; double ans[50][50]={0},r; //记录查询int n,num,s1,s2,same,tmp,sp1,sp2;scanf("%d",&n);for(int i=0;i<n;i++){scanf("%d",&arr[i][10000]);for(int j=0;j<arr[i][10000];j++){scanf("%d",&arr[i][j]);}sort(arr[i],arr[i]+arr[i][10000]); arr[i][10000]=unique(arr[i],arr[i]+arr[i][10000])-arr[i]; //去重}scanf("%d",&n);while(n--){scanf("%d %d",&s1,&s2);if(ans[s1-1][s2-1]!=0) {printf("%.2f%\n",ans[s1-1][s2-1]);continue;}same=0;sp1=sp2=0;while(sp1<arr[s1-1][10000]&&sp2<arr[s2-1][10000]) {//指针if(arr[s1-1][sp1]<arr[s2-1][sp2])sp1++;else if(arr[s1-1][sp1]>arr[s2-1][sp2])sp2++;else{same++;sp1++;sp2++;}}r=same*100.0/(arr[s1-1][10000]+arr[s2-1][10000]-same); //计算ans[s1-1][s2-1]=ans[s2-1][s1-1]=r;printf("%.2f%\n",r);}return 0;
}②数组,取交集函数;/2119-438ms/
#include <bits/stdc++.h>using namespace std;int main()
{set<int> l[51];double ans[50][50]={0};int n,g,i,m,p,q,cou;scanf("%d",&n);for(i=1;i<=n;i++){scanf("%d",&m);while(m--){scanf("%d",&g);l[i].insert(g);}}scanf("%d",&n);while(n--){set<int>s;cou=0;scanf("%d%d",&p,&q);if(ans[p-1][q-1]>=0.0001){printf("%.2lf%%\n", ans[p-1][q-1]);}else{set_intersection(l[p].begin(),l[p].end(),l[q].begin(),l[q].end(),inserter(s,s.begin()));int cou = s.size();ans[p-1][q-1]=ans[q-1][p-1]=cou*100.0/(l[p].size()+l[q].size()-cou);printf("%.2lf%%\n", ans[p-1][q-1]);}}return 0;
}
③被TLE毙掉的:unordered_map模拟桶排,查找键值。/2119-252ms/
#include <bits/stdc++.h>using namespace std;int main()
{int a[51]= {0};double ans[50][50]={0};unordered_map<int,bool> s[51];unordered_map<int,bool>::iterator it;int n,g,i,m,p,q,cou;scanf("%d",&n);for(i=1; i<=n; i++){scanf("%d",&m);a[i]=m;while(m--){scanf("%d",&g);if(!s[i][g])s[i][g]=1;else a[i]--;}}scanf("%d",&n);while(n--){cou=0;scanf("%d%d",&p,&q);if(ans[p-1][q-1]>=0.0001){printf("%.2lf%%\n", ans[p-1][q-1]);}else{if(a[p]>a[q])swap(p,q);for(it=s[p].begin(); it!=s[p].end(); it++)if(s[q].find(it->first)!=s[q].end()){cou++;}ans[p-1][q-1]=ans[q-1][p-1]=cou*100.0/(a[p]+a[q]-cou);printf("%.2lf%%\n", ans[p-1][q-1]);}}return 0;
}
②慢于③的可能原因的2119数据量太小
①慢于数组桶排的原因可能是①的实际运行时间是2*min(m , n),桶排的实际运行时间取决于数据范围。
ED
这两道题我一共submit 58次!!!
AC率不用要了555。
这篇关于关于 相似的数集 的思路+时间复杂度分析+代码的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




