[硫化铂]好

2024-03-16 22:32

文章标签 硫化

本文主要是介绍[硫化铂]好，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

乐

题目概述

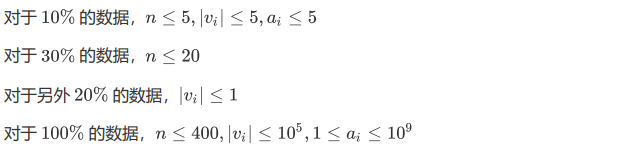
在这里插入图片描述

题解

首先， $\text\color{black}{O}\color{red}{neInDark}$ :对于这种每次删一个连续段的问题，我们应该很容易想到区间dp。
首先，我们可以发现合法的连续段是呈现一个单峰的态势，即只存在一个点比
旁边的两个点都高，其它的都是在两个点的中点处。
我们可以定义 $dp_{l,r}$ 表示将区间分解成若干的合法序列，最后全部删去得到的最大代价。
显然，其有两种转移，一是有两个全部删完的区间拼起来，二是有一个从 $l$ 到 $r$ 的合法序列，中间穿插了许多合法区间。
显然，第一个只需要枚举一个分界点就可以转移了。
而对于第二种情况的转移，我们可以去枚举的个单峰的位置。
显然，这个单峰左侧是一个上升序列，而右侧是一个下降序列，我们要在这中间穿插一些合法序列。
那么我们显然可以定义另一个 $d p$ 数组用于转移这个上升序列与下降序列，然后再将这两个序列拼起来就可以得到整个要删去的序列。
我们知道这个序列的左端点，右端点，峰值，而相邻两个点相差为 $1$ ，那么就可以很简单的计算出这个序列的长度，知道其贡献。
最后，再整一个 $d p$ 将所有不相邻的合法区间合并起来即可。

时间复杂度 $O\left(n^3\right)$ 。

源码

#include<bits/stdc++.h>
using namespace std;
#define MAXN 405
#define MAXM (1<<20)+5
#define lowbit(x) (x&-x)
#define reg register
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
#define lson (rt<<1)
#define rson (rt<<1|1)
typedef long long LL;
typedef unsigned long long uLL; 
typedef long double ld;
typedef pair<int,int> pii;
const int INF=0x3f3f3f3f;
const int mo=998244353;
const int mod=1e5+3;
const int inv2=499122177;
const int jzm=2333;
const int zero=2000;
const int n1=1000;
const int M=100000;
const int orG=3,ivG=332748118;
const long double Pi=acos(-1.0);
const double eps=1e-12;
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
template<typename _T>
void read(_T &x){_T f=1;x=0;char s=getchar();while(s>'9'||s<'0'){if(s=='-')f=-1;s=getchar();}while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}x*=f;
}
template<typename _T>
void print(_T x){if(x<0){x=(~x)+1;putchar('-');}if(x>9)print(x/10);putchar(x%10+'0');}
int gcd(int a,int b){return !b?a:gcd(b,a%b);}
int add(int x,int y,int p){return x+y<p?x+y:x+y-p;}
void Add(int &x,int y,int p){x=add(x,y,p);}
int qkpow(int a,int s,int p){int t=1;while(s){if(s&1)t=1ll*t*a%p;a=1ll*a*a%p;s>>=1;}return t;}
int n,a[405],val[405],dp[405][405],pre[405][405],suf[405][405],gp[405];
signed main(){freopen("good.in","r",stdin);freopen("good.out","w",stdout);read(n);for(int i=1;i<=n;i++)read(val[i]);for(int i=1;i<=n;i++)read(a[i]);for(int len=1;len<=n;len++)for(int l=1,r=len;r<=n;l++,r++){bool flag=0;for(int i=l+1;i<=r;i++){if(Fabs(a[i]-a[i-1])^1){flag=1;break;}if(i<r&&a[i]+a[i]<a[i-1]+a[i+1]){flag=1;break;}}if(!flag)dp[l][r]=val[len];else dp[l][r]=-INF;if(l==r){pre[l][r]=suf[r][l]=0;continue;}pre[l][r]=suf[r][l]=-INF;for(int j=l;j<r;j++)if(a[j]+1==a[r])pre[l][r]=max(pre[l][j]+dp[j+1][r-1],pre[l][r]);for(int j=r;j>l;j--)if(a[j]+1==a[l])suf[r][l]=max(suf[r][j]+dp[l+1][j-1],suf[r][l]);for(int j=l;j<=r;j++){if(pre[l][j]<1-INF||suf[r][j]<1-INF)continue;dp[l][r]=max(dp[l][r],pre[l][j]+suf[r][j]+val[a[j]+a[j]-a[l]-a[r]+1]);}for(int mid=l;mid<r;mid++)dp[l][r]=max(dp[l][r],dp[l][mid]+dp[mid+1][r]);}gp[0]=0;for(int i=1;i<=n;i++){gp[i]=gp[i-1];for(int j=i;j>0;j--)gp[i]=max(gp[i],gp[j-1]+dp[j][i]);}printf("%d\n",gp[n]);return 0;
}