[硫化铂]序排速快

2024-03-16 22:32

文章标签 硫化序排速快

本文主要是介绍[硫化铂]序排速快，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

序排速快

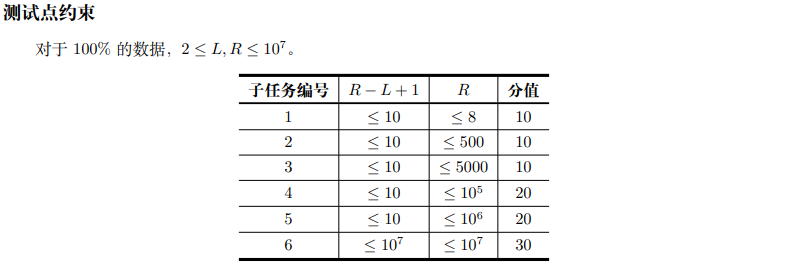
在这里插入图片描述

题解

首先，对于原题的分割点定义，我们可以实质上是可以把它看成两个点之间的一条线。
当该线的左边数的最大值小于右边数的最小值时该分割点会成立，也就是说，之后不会有任何一个冒泡排序的范围能跨越这道分割线。
事实上，如果我们直接去统计一个分割线的出现时间的话是对计算答案没什么效果，但我们可以发现我们可以从点的层面上计算答案。
一个相当经典的技巧，我们可以计算一个点被进行了冒泡排序多少次。
显然，当一个点两边的分割线都出现时，它的位置就已经被固定了，今后也不会再参与任何一次冒泡排序，对答案产生任何的贡献了。而再此前，它是会参与冒泡排序的。
我们考虑计算一个分割线会经过几次冒泡排序消失。
不妨记 $p_i$ 为权值不超过分割线 $i$ 的点最远的距离，显然 $p_i\geqslant i$ ，我们发现，一次冒泡排序，铁定会使 $p_i-1$ ，除非它已经变为 $0$ ，否则肯定会有点冲到它前面去。
于是，可以知道分割线 $i$ 的出现时间 $t_i=p_{i}-i$ ，那么一个排列的答案就是 $\sum_{i=2}^{n}\max(t_{i-1},t_{i})$ 。

我们可以将原答案分为两种情况， $t_{i-1}\leqslant t_{i}$ 时，贡献 $t_i$ ；当 $t_{i-1}>t_i$ 时，贡献 $t_{i-1}$ 。
可以发现，.
$t_{i-1}\leqslant t_{i}\Leftrightarrow p_{i-1}<p_i$ ，即 $i$ 出现在 $[1, i - 1]$ 所有数的右边。
$t_{i-1}>t_i\Leftrightarrow p_{i-1}\geqslant p_i$ ，即 $[1, i - 1]$ 中有一个数出现在 $i$ 右边。
枚举每个数的贡献，可以得到第一种情况的贡献，
$sum_1=\sum_{i=1}^{n}\sum_{j=1}^{i} (i-j)\binom{i-1}{j-1}(j-1)!(n-j)!$ 同理，可以得到第二种情况的贡献，
$sum_2=\sum_{i=1}^{n}\sum_{j=1}^{i} (i-j+1)\binom{i-1}{j-1}(j-1)(j-1)!(n-j)!$ 将其相加，可以得到总答案，顺便改变一下 $i, j$ 的枚举顺序，
$ans=\sum_{i=1}^{n}\sum_{j=i}^{n}(ij-j^2+j-1)\binom{j-1}{i-1}(i-1)!(n-i)!$ 不妨将含 $i$ 的项与不含 $i$ 的项分开计算，那么有
$ans_1=\sum_{i=1}^n\sum_{j=i}^nij\frac{(j-1)!}{(i-1)!(j-i)!}(i-1)!(n-i)!=\sum_{i=1}^n\sum_{j=i}^ni(n-i)!i!\frac{j!}{(j-i)!i!}\\ =\sum_{i=1}^ni(n-i)!i!\sum_{j=i}^n\binom{j}{i}=\sum_{i=1}^ni(n-i)!i!\binom{n+1}{i+1}=(n+1)!\sum_{i=1}^n\frac{i}{i+1}\\ ans_2=\sum_{i=1}^n\sum_{j=i}^n(-j^2+j-1)\binom{j-1}{i-1}(i-1)!(n-i)!=\sum_{i=1}^n\sum_{j=i}^n(-j^2+j-1)(i-1)!(n-i)!\frac{(j-1)!}{(i-1)!(j-i)!}\\ =\sum_{i=1}^n\sum_{j=1}^i(-i^2+i-1)(i-1)!(n-i)!\frac{(n-j)!}{(i-j)!(n-i)!}=\sum_{i=1}^n(-i^2+i-1)(i-1)!(n-i)!\sum_{j=1}^i\binom{n-j}{n-i}\\ =\sum_{i=1}^n(-i^2+i-1)(i-1)!(n-i)!\binom{n}{i}=n!\sum_{i=1}^n\frac{-i^2+i-1}{i}$ 显然，上面这两者都是可以线性递推求解的，于是我们只需要预处理一下阶乘与逆元就可以快速计算 $n\in[L,R]$ 中的所有情况了。

时间复杂度 $O\left(R\right)$ 。

源码

~~这还需要贴吗？~~

#include<bits/stdc++.h>
using namespace std;
#define MAXN 10000005
#define lowbit(x) (x&-x)
#define reg register
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
#define lson (rt<<1)
#define rson (rt<<1|1)
typedef long long LL;
typedef unsigned long long uLL; 
typedef long double ld;
typedef pair<int,int> pii;
const int INF=0x3f3f3f3f;
const int mo=998244353;
const int mod=1e5+3;
const int inv2=5e8+4;
const int jzm=2333;
const int zero=2000;
const int n1=1000;
const int M=100000;
const int orG=3,ivG=332748118;
const long double Pi=acos(-1.0);
const double eps=1e-12;
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
template<typename _T>
void read(_T &x){_T f=1;x=0;char s=getchar();while(s>'9'||s<'0'){if(s=='-')f=-1;s=getchar();}while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}x*=f;
}
template<typename _T>
void print(_T x){if(x<0){x=(~x)+1;putchar('-');}if(x>9)print(x/10);putchar(x%10+'0');}
int gcd(int a,int b){return !b?a:gcd(b,a%b);}
int add(int x,int y,int p){return x+y<p?x+y:x+y-p;}
void Add(int &x,int y,int p){x=add(x,y,p);}
int qkpow(int a,int s,int p){int t=1;while(s){if(s&1)t=1ll*t*a%p;a=1ll*a*a%p;s>>=1;}return t;}
int n,L,R,fac[MAXN],inv[MAXN],ff[MAXN],answer;
void init(){fac[0]=fac[1]=inv[0]=inv[1]=ff[1]=1;for(int i=2;i<=R+1;i++)fac[i]=1ll*i*fac[i-1]%mo,ff[i]=1ll*(mo-mo/i)*ff[mo%i]%mo,inv[i]=1ll*ff[i]*inv[i-1]%mo;
}
int C(int x,int y){if(x<0||y<0||x<y)return 0;return 1ll*fac[x]*inv[y]%mo*inv[x-y]%mo;
}
signed main(){//freopen("tros.in","r",stdin);//freopen("tros.out","w",stdout);read(L);read(R);init();int sum1=0,sum2=0;for(int i=1;i<=R;i++){Add(sum1,1ll*i*ff[i+1]%mo,mo);Add(sum2,1ll*add(i-1,mo-1ll*i*i%mo,mo)*ff[i]%mo,mo);int ans=add(1ll*fac[i+1]*sum1%mo,1ll*fac[i]*sum2%mo,mo);if(i>=L)answer^=ans;}printf("%d\n",answer);return 0;
}