[硫化铂]膜拜大丹

本文主要是介绍[硫化铂]膜拜大丹，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

膜拜大丹

在这里插入图片描述

题解

首先我们可以观察到一个性质，我们一定只会走二元环。
整张图是一个二分图，我们每次是从一边跳到另一边，所以走过的路径一定是一个偶环。
我们不妨记我们走过的路径为 $A_{p_1}\rightarrow B_{q_1}\rightarrow A_{p_2}\rightarrow B_{q_2}\rightarrow...\rightarrow B_{q_n}\rightarrow A_{p_{n+1}}$ ，其中 $p_{n+1}=p_1$ ，那么一定存在一个时刻有 $p_i < p_{i+1}$ 让我们从 $A_{p_i}$ 走到 $B_{q_i}$ 再走到 $A_{p_{i+1}}$ 。
显然，此时我一定可以走二元环 $A_{p_i}\rightarrow B_{q_i}\rightarrow A_{p_i}$ ，这样显然是不比上面的环劣的，因为一个环里的每个点都只会有一的贡献。
所以我们就可以将原问题转化成找到数量最多的二元环匹配。

上面的问题显然是可以使用网络流解决的，但对于 $n\leqslant 5\times 10^5$ 的数据范围来说显然不大合理。
我们可以考虑将问题转化一下，想象一个网格图，上面有 $i,a_i),(b_i,i)$ 这两类点。
如果两个点能够匹配，显然是 $i,a_i)$ 与 $b_i,i)$ 向各自对应的坐标轴做垂线有交点。
当然，我们要找的是这些点的最大匹配，可以将其转化成找最大独立集，减去就得到最大匹配。
考虑两个点在怎样的情况下是独立的，显然是两个点的垂线没有交点。
我们把 $i,a_i)$ 看成红点， $b_i,i)$ 看成绿点，那么如果我们用一条路径划分图内的红绿点，当然这条路径自会向上与向右走，那么在路径上方的红点与路径下方的绿点就是独立的。
我们要用这种划分的方法使得我们上方的红点数与下方的绿点数相加的总和最大。
大概就是这样的，
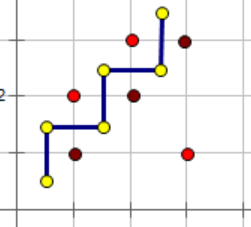
在这里插入图片描述
红绿点可能不大好区分，不过应该能理解，这样是 $2 + 3 = 5$ ，独立集是最大的，那么他的最大匹配就是 $1$ 。

显然，这样的最大匹配我们是可以用 $d p$ 来求的。
记 $dp_{i,j}$ 表示我们的路径现在走到了 $(i, j)$ 这个格子时，我们得到的独立集的最大值。
转移很显然，向右走是判断当前的 $b_j,j)$ 能不能加入，向上走时就判断 $i,a_i)$ 能不能加入。显然只要我们的路径不与它们的垂线相交就可以加入。
如果直接 $d p$ 的话是 $O\left(nm\right)$ 的，但我们显然是可以进行优化的。
显然，如果我们确定一部分红点要选，现在考虑
我们发现，当我们的高度超过 $b_i$ 就不会再对 $b_i,i)$ 造成影响了，而在达到 $b_i$ 之前，如果向右走已经已经超过 $i$ ，那么 $b_i,i)$ 就不会产生贡献。
所以这是对于所有 $j < i$ 的 $dp_{k,j}$ ，我们是会对其产生一的贡献，整体加一。
而对于我们的 $i,a_i)$ ，如果我们要将它加入进去转移的话，相当于至少要让我们的第二维达到 $a_i$ ，也就是说， $\geqslant a_i$ 的部分可以 $+ 1$ ，当然要注意 $\leqslant a_i$ 的部分可以从这一层走到 $a_i$ ，再 $+ 1$ 。
不过事实上每个点的权值并不是只有 $1$ 的，应该是 $c_i$ 和 $d_i$ ，因为他有多个点在一起吗，不过考虑时可以按将其拆成点权个点，方便思考。
容易发现上面我们的 $d p$ 转移式容易用线段树来进行维护的，所以打一棵线段树就可以维护了。

时间复杂度 $O\left(n\log\,n\right)$ 。

源码

#include<bits/stdc++.h>
using namespace std;
#define MAXN 500005
#define MAXM (1<<20)+5
#define lowbit(x) (x&-x)
#define reg register
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
#define lson (rt<<1)
#define rson (rt<<1|1)
typedef long long LL;
typedef unsigned long long uLL; 
typedef long double ld;
typedef pair<int,int> pii;
const int INF=0x3f3f3f3f;
const int mo=998244353;
const int mod=1e5+3;
const int inv2=5e8+4;
const int jzm=2333;
const int zero=2000;
const int n1=1000;
const int M=100000;
const int orG=3,ivG=332748118;
const long double Pi=acos(-1.0);
const double eps=1e-12;
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
template<typename _T>
void read(_T &x){_T f=1;x=0;char s=getchar();while(s>'9'||s<'0'){if(s=='-')f=-1;s=getchar();}while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}x*=f;
}
template<typename _T>
void print(_T x){if(x<0){x=(~x)+1;putchar('-');}if(x>9)print(x/10);putchar(x%10+'0');}
int gcd(int a,int b){return !b?a:gcd(b,a%b);}
int add(int x,int y,int p){return x+y<p?x+y:x+y-p;}
void Add(int &x,int y,int p){x=add(x,y,p);}
int qkpow(int a,int s,int p){int t=1;while(s){if(s&1)t=1ll*t*a%p;a=1ll*a*a%p;s>>=1;}return t;}
int n,m,a[MAXN],b[MAXN],c[MAXN],d[MAXN],ord[MAXN];LL ans,summ;
class SegmentTree{private:LL tr[MAXN<<2],lzy[MAXN<<2],cov[MAXN<<2];void pushup(int rt){tr[rt]=max(tr[lson],tr[rson]);}void pushdown(int rt){if(lzy[rt]){tr[lson]+=lzy[rt];lzy[lson]+=lzy[rt];cov[lson]+=lzy[rt];tr[rson]+=lzy[rt];lzy[rson]+=lzy[rt];cov[rson]+=lzy[rt];lzy[rt]=0;}if(cov[rt]){tr[lson]=max(tr[lson],cov[rt]);cov[lson]=max(cov[lson],cov[rt]);tr[rson]=max(tr[rson],cov[rt]);cov[rson]=max(cov[rson],cov[rt]);cov[rt]=0;}}public:void insert(int rt,int l,int r,int al,int ar,LL aw){if(l>r||l>ar||r<al||al>ar)return ;if(al<=l&&r<=ar){tr[rt]+=aw;lzy[rt]+=aw;cov[rt]+=aw;return ;}int mid=l+r>>1;pushdown(rt);if(al<=mid)insert(lson,l,mid,al,ar,aw);if(ar>mid)insert(rson,mid+1,r,al,ar,aw);pushup(rt); }void modify(int rt,int l,int r,int al,int ar,LL aw){if(l>r||l>ar||r<al||al>ar)return ;if(al<=l&&r<=ar){tr[rt]=max(tr[rt],aw);cov[rt]=max(cov[rt],aw);return ;}int mid=l+r>>1;pushdown(rt);if(al<=mid)modify(lson,l,mid,al,ar,aw);if(ar>mid)modify(rson,mid+1,r,al,ar,aw);pushup(rt);}LL query(int rt,int l,int r,int al,int ar){if(l>r||l>ar||r<al||al>ar)return 0;if(al<=l&&r<=ar)return tr[rt];int mid=l+r>>1;LL res=0;pushdown(rt);if(al<=mid)res=max(res,query(lson,l,mid,al,ar));if(ar>mid)res=max(res,query(rson,mid+1,r,al,ar));return res;}
}T;
bool cmp(int x,int y){return b[x]<b[y];}
signed main(){//freopen("worship.in","r",stdin);//freopen("worship.out","w",stdout);read(n);read(m);for(int i=1;i<=n;i++)read(a[i]);for(int i=1;i<=m;i++)read(b[i]);for(int i=1;i<=n;i++)read(c[i]),summ+=c[i];for(int i=1;i<=m;i++)read(d[i]),summ+=d[i];if(n>m){for(int i=1;i<=n;i++)swap(a[i],b[i]),swap(c[i],d[i]);swap(n,m);}for(int i=1;i<=m;i++)ord[i]=i;sort(ord+1,ord+m+1,cmp);int j=1;for(int i=1;i<=n;i++){while(j<=m&&b[ord[j]]<i)T.insert(1,0,m,0,ord[j]-1,d[ord[j]]),j++;T.insert(1,0,m,a[i],m,c[i]);LL tmp=T.query(1,0,m,0,a[i]-1)+c[i];T.modify(1,0,m,a[i],m,tmp);}while(j<=m)T.insert(1,0,m,0,ord[j]-1,d[ord[j]]),j++;printf("%lld\n",summ-T.query(1,0,m,0,m));return 0;
}