[硫化铂]传染

本文主要是介绍[硫化铂]传染，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

传染

题目描述

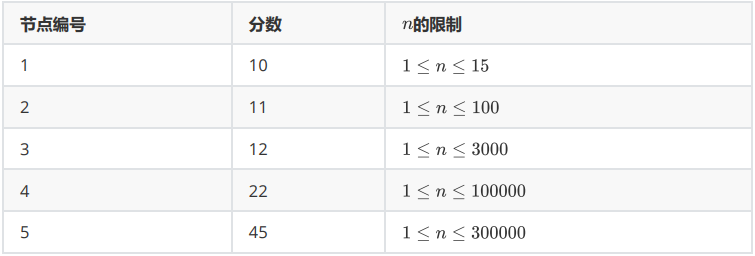
题解

可以发现，我们可以将原题转化成在一张图上选几个点，使之可以覆盖整个图。
每个点可以向与它距离不超过$r_i$的点连一条单向边，使得我们选的所有点可以到达图上任意一个点。
那么我们显然可以直接将这个图建出来，然后观察一下这个图。
首先，对于一个边双联通分量中，显然任意两个点都是可以互相覆盖的，所以一个边双联通分量中最多选择一个点，我们不妨先缩一下点。
之后我们得到的就是一个拓扑图了，显然此时选择所有入度为$0$的点就可以覆盖整张图，它们又不可能被别的点覆盖，所以肯定是最小的。
这样的由于总边数可能会达到$n^2$，所以复杂度是$O\left(n^2\right)$。

显然上面的做法是可以优化的，毕竟我们并不需要用到这么多边。
我们考虑一条从$s\to t$的路径，显然，如果这条路径的长度是不超过$r_s$的，那么点$s$就会向点$t$连边。
一条路径上肯定存在且仅存在一个点使得这个点在点分树上的整个子树能够覆盖这条路径，我们可以考虑这这个点处连接我们的这条边。
如果我们在点分树上的点$x$上考虑点$y$的边，如果要与点$z$在这个点上连边，那么我们会把这个点$x$当作我们点$y$与点$z$的$lca$。
也就是说，这条路径的长度是$de{p}_y+de{p}_z-2de{p}_x$，当这个长度不超过$r_y$时，$y$就会与$z$连边。
调换一下顺序，也就是满足条件$r_y-de{p}_y+de{p}_x⩾de{p}_z-de{p}_x$时，会与边，如果我们固定点$x$为当前子树的根的话，那么这两边就只与自己本身的$y$或$z$有关了。
而这种大于关系，显然可以看成一个前缀，那我们可以考虑建虚点到达这些前缀，然后$y$就直接向这个这个虚点连边，反正覆盖是可传递的，这样就可以实现原来所有跨越这个点的边。
这样的话，我们边数就被降到$O\left(n\log n\right)$级别了，不过点数还是$O\left(n\log n\right)$级别的，不过还是开得下。

由于每层都要将子树内所有的点排遍序，虽然可以做些小优化，不过也不会很卡。
时间复杂度$O\left(n{\log }^{2}n\right)$。

源码

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#include<bits/stdc++.h>
using namespace std;
#define MAXN 300005
#define MAXM 6000005
#define lowbit(x) (x&-x)
#define reg register
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
#define lson (rt<<1)
#define rson (rt<<1|1)
typedef long long LL;
typedef unsigned long long uLL; 
typedef long double ld;
typedef pair<int,int> pii;
const int INF=0x3f3f3f3f;
const int mo=998244353;
const int mod=1e5+3;
const int inv2=499122177;
const int jzm=2333;
const int zero=2000;
const int n1=1000;
const int M=100000;
const int orG=3,ivG=332748118;
const long double Pi=acos(-1.0);
const double eps=1e-12;
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
template<typename _T>
void read(_T &x){_T f=1;x=0;char s=getchar();while(s>'9'||s<'0'){if(s=='-')f=-1;s=getchar();}while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}x*=f;
}
template<typename _T>
void print(_T x){if(x<0){x=(~x)+1;putchar('-');}if(x>9)print(x/10);putchar(x%10+'0');}
int gcd(int a,int b){return !b?a:gcd(b,a%b);}
int add(int x,int y,int p){return x+y<p?x+y:x+y-p;}
void Add(int &x,int y,int p){x=add(x,y,p);}
int qkpow(int a,int s,int p){int t=1;while(s){if(s&1)t=1ll*t*a%p;a=1ll*a*a%p;s>>=1;}return t;}
int n,head[MAXN],tot,sta[MAXM],stak,ans,deg[MAXM],totp;
int dfn[MAXM],low[MAXM],belong[MAXM],idx,cnt;
int all,mx,Rt,siz[MAXN],mxson[MAXN],ord[MAXN],A[MAXN],B[MAXN];
bool vis[MAXN],insta[MAXM];
LL val[MAXN],dep[MAXN],maxx[MAXN];
vector<int>G[MAXM];
struct edge{int to,nxt;LL paid;}e[MAXN<<1];
void addEdge(int u,int v,LL w){e[++tot]=(edge){v,head[u],w};head[u]=tot;}
void getRoot(int u,int fa){siz[u]=1;mxson[u]=0;for(int i=head[u];i;i=e[i].nxt){int v=e[i].to;if(v==fa||vis[v])continue;getRoot(v,u);siz[u]+=siz[v];mxson[u]=max(mxson[u],siz[v]);}mxson[u]=max(mxson[u],all-siz[u]);if(mxson[u]<mx)Rt=u,mx=mxson[u];
}
void dosaka(int u,int fa,LL Mx,LL Mn){siz[u]=1;if(Mx<0||Mn<val[u])ord[++idx]=u;if(fa)Mx=max(Mx,val[u]),Mn=max(Mn,val[u]);for(int i=head[u];i;i=e[i].nxt){int v=e[i].to;if(v==fa||vis[v])continue;dep[v]=dep[u]+e[i].paid;dosaka(v,u,Mx-e[i].paid,Mn+e[i].paid);siz[u]+=siz[v];}
}
bool cmp1(int x,int y){return val[x]-dep[x]>val[y]-dep[y];}
bool cmp2(int x,int y){return dep[x]>dep[y];}
void sakura(int rt){mx=INF;getRoot(rt,0);dep[Rt]=idx=0;dosaka(Rt,0,-1,-1);vis[Rt]=1;int las=0,j=1;for(int i=1;i<=idx;i++)A[i]=B[i]=ord[i];sort(A+1,A+idx+1,cmp1);sort(B+1,B+idx+1,cmp2);for(int i=1;i<=idx;i++){int x=A[i];bool flag=0;while(j<=idx&&dep[x]+dep[B[j]]>val[x]){if(las)G[las].pb(B[j]),flag=1;j++;}int now=++totp;if(las)G[las].pb(now);G[x].pb(now);las=now;}while(j<=idx){if(las)G[las].pb(B[j]);j++;}for(int i=head[Rt];i;i=e[i].nxt){int v=e[i].to;if(vis[v])continue;all=siz[v];sakura(v);}
}
void tarjan(int u){dfn[u]=low[u]=++idx;sta[++stak]=u;insta[u]=1;int siz=G[u].size();for(int i=0;i<siz;i++){int v=G[u][i];if(!dfn[v])tarjan(v),low[u]=min(low[u],low[v]);else if(insta[v])low[u]=min(low[u],dfn[v]);}if(dfn[u]==low[u]){int v;cnt++;do{v=sta[stak--];insta[v]=0;belong[v]=cnt;}while(u^v);}
}
signed main(){//freopen("infect.in","r",stdin);//freopen("infect.out","w",stdout);read(n);totp=n;for(int i=1;i<=n;i++)read(val[i]);for(int i=1;i<n;i++){int u,v;LL w;read(u);read(v);read(w);addEdge(u,v,w);addEdge(v,u,w);}all=n;sakura(1);idx=0;for(int i=1;i<=totp;i++)if(!dfn[i])tarjan(i);for(int u=1;u<=totp;u++){int siz=G[u].size();for(int i=0;i<siz;i++){int v=G[u][i];if(belong[u]^belong[v])deg[belong[v]]++;}}for(int i=1;i<=cnt;i++)if(!deg[i])ans++;printf("%d\n",ans);return 0;
}

谢谢！！！

这篇关于[硫化铂]传染的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---