算法打卡day18|二叉树篇07|Leetcode 530.二叉搜索树的最小绝对差、501.二叉搜索树中的众数、236. 二叉树的最近公共祖先

本文主要是介绍算法打卡day18|二叉树篇07|Leetcode 530.二叉搜索树的最小绝对差、501.二叉搜索树中的众数、236. 二叉树的最近公共祖先，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

算法题

Leetcode 530.二叉搜索树的最小绝对差

题目链接:530.二叉搜索树的最小绝对差

大佬视频讲解：二叉搜索树的最小绝对差视频讲解

个人思路

因为是在二叉搜索树求绝对差，而二叉搜索树是有序的，那就把它想成在一个有序数组上求最值，求差值。采用中序遍历的递归，遍历所有节点，求出最小值

解法

递归法

使用二叉搜索树的特性，利用中序遍历就能把二叉树按照递增序列去遍历，如下图；

class Solution {TreeNode pre;// 记录上一个遍历的结点int result = Integer.MAX_VALUE;//存最小绝对值的结果public int getMinimumDifference(TreeNode root) {if(root==null)return 0;traversal(root);return result;}public void traversal(TreeNode root){if(root==null)return;//终止条件traversal(root.left); //左if(pre!=null){ //中result = Math.min(result,root.val-pre.val);//取差值绝对值最小}pre = root;traversal(root.right);//右}
}

时间复杂度:O(n)；（遍历整棵树）

空间复杂度:O(n);（递归树的高度，如果是一个高度不平衡的树（例如链状结构）高度与n接近）

迭代法

中序遍历的迭代法模板，再加上前一个节点pre，遍历取最小绝对值；

class Solution {TreeNode pre;Stack<TreeNode> stack;public int getMinimumDifference(TreeNode root) {if (root == null) return 0;stack = new Stack<>();//模拟递归的栈TreeNode cur = root;//当前节点int result = Integer.MAX_VALUE;while (cur != null || !stack.isEmpty()) {if (cur != null) {stack.push(cur); // 将访问的节点放进栈cur = cur.left; // 左}else {cur = stack.pop(); if (pre != null) { // 中result = Math.min(result, cur.val - pre.val);}pre = cur;//上一个节点cur = cur.right; // 右}}return result;}
}

时间复杂度:O(n)；（遍历整棵树）

空间复杂度:O(n);(递归栈的空间）

Leetcode 501.二叉搜索树中的众数

题目链接:501.二叉搜索树中的众数

大佬视频讲解:二叉搜索树中的众数视频讲解

个人思路

又是二叉搜索树，所以可以使用中序遍历使得遍历顺序为递增顺序，这样比较出现频率就可以和相邻的值比较（比较时可以使用pre指针和cur指针），最后就把出现频率最高的元素输出；

解法

递归法

这道题只需要遍历一次就可以找到所有的众数。

在遍历时，如果频率count 等于 maxCount（最大频率），把这个元素加入到结果集中；频率count 大于 maxCount的时候，不仅要更新maxCount，而且要清空结果集，因为结果集之前的元素都失效了。

class Solution {ArrayList<Integer> resList;//结果集int maxCount;//最大出现频次int count;//当前节点频次TreeNode pre;//用来比较节点值是否相同public int[] findMode(TreeNode root) {resList = new ArrayList<>();maxCount = 0;count = 0;pre = null;//初始为空findMode1(root);int[] res = new int[resList.size()];for (int i = 0; i < resList.size(); i++) {res[i] = resList.get(i);}return res;}public void findMode1(TreeNode root) {if (root == null) {return;}findMode1(root.left);int rootValue = root.val;if (pre == null || rootValue != pre.val) { // 计数count = 1;} else {count++;}// 更新结果以及maxCountif (count > maxCount) {resList.clear();//清空失效的结果集resList.add(rootValue);//加入新的结果maxCount = count;} else if (count == maxCount) {resList.add(rootValue);}pre = root;findMode1(root.right);}
}

时间复杂度:O(n)；（最差遍历一遍树）

空间复杂度:O(n);（递归树的高度h，结果集最多为n）

迭代法

使用栈模拟递归，

class Solution {public int[] findMode(TreeNode root) {TreeNode pre = null;Stack<TreeNode> stack = new Stack<>();List<Integer> result = new ArrayList<>();int maxCount = 0;int count = 0;TreeNode cur = root;while (cur != null || !stack.isEmpty()) {if (cur != null) {stack.push(cur);cur =cur.left;//左}else {cur = stack.pop();//中// 计数if (pre == null || cur.val != pre.val) {count = 1;}else {count++;}// 更新结果if (count > maxCount) {maxCount = count;result.clear();result.add(cur.val);}else if (count == maxCount) {result.add(cur.val);}pre = cur;cur = cur.right;//右}}//列表转数组，即result 列表中所有 Integer 元素转换为原始整数值的 int 类型数组。return result.stream().mapToInt(Integer::intValue).toArray();}
}

时间复杂度:O(n)；（遍历整棵树）

空间复杂度:O(n);（使用栈，结果集大小）

Leetcode 236. 二叉树的最近公共祖先

题目链接:236. 二叉树的最近公共祖先

大佬视频讲解:二叉树的最近公共祖先视频讲解

个人思路

思路不清晰，主要是如何递归不太清楚。

解法

递归法

首先确定采用后序遍历，因为是需要找出公共祖先，所以先遍历左右节点，然后递归三步走

1.确定递归函数返回值以及参数

需要递归函数返回值，来说明是否找到节点q或者p，那么返回值为bool类型就可以了。

但还要返回最近公共节点，可以利用上题目中返回值是TreeNode * ，那么如果遇到p或者q，就把q或者p返回，返回值不为空，就说明找到了q或者p。

2.确定终止条件

遇到空的话，因为树都是空了，所以返回空。

如果 root == q，或者 root == p，说明找到 q p ，则将其返回

3.确定单层递归逻辑

如果递归函数有返回值，搜索一条边和搜索整个树是有区别

搜索一条边的写法：

if (递归函数(root->left)) return ;if (递归函数(root->right)) return ;

搜索整个树写法：

left = 递归函数(root->left);  // 左
right = 递归函数(root->right); // 右
left与right的逻辑处理;         // 中

在递归函数有返回值的情况下：如果要搜索一条边，递归函数返回值不为空的时候，立刻返回，如果搜索整个树，直接用一个变量left、right接住返回值，这个left、right后续还有逻辑处理的需要，也就是后序遍历中处理中间节点的逻辑（也是回溯）。

在这道题中，还要遍历根节点右子树（即使此时已经找到了目标节点了），因为要等left与right逻辑处理完之后才能返回。

其中处理left和right的逻辑如下：

如果left 和 right都不为空，说明此时root就是最近公共节点。

如果left为空，right不为空，就返回right，说明目标节点是通过right返回的，反之依然。如下图

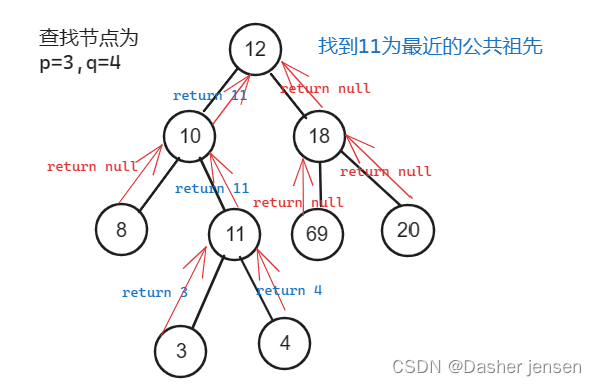
class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if (root == null || root == p || root == q) { // 递归结束条件return root;}TreeNode left = lowestCommonAncestor(root.left, p, q);TreeNode right = lowestCommonAncestor(root.right, p, q);if(left == null && right == null) { // 若未找到节点 p 或 qreturn null;}else if(left == null && right != null) { // 若找到一个节点return right;}else if(left != null && right == null) { // 若找到一个节点return left;}else { // 若找到两个节点return root;}}
}