VINS-MONO理论学习---紧耦合后端非线性优化

基于滑动窗的紧耦合后端非线性优化：将视觉约束、IMU约束、闭环约束放到一个大的目标函数中进行非线性优化，求解出滑动窗口中所有帧的PVQ、bias等。

在视觉约束和IMU约束中，基本思想是找到优化状态向量，然后通过视觉残差和IMU测量残差分别对状态向量求导，获得视觉和IMU预积分的Jacobian和协方差矩阵。

一、VIO残差函数的构建

1、需要优化的状态向量：
状态向量包括滑动窗口内的所有相机状态（位置P、旋转Q、速度V、加速度偏置ba、陀螺仪偏置bw）、相机到IMU的外参、所有3D点的逆深度：

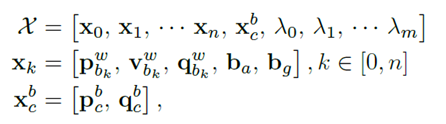
第一个式子是滑动窗口内所有状态量，n是关键帧数量，m是滑动窗内所有观测到的路标点总数，维度是15*n+6+m。特征点逆深度为了满足高斯系统。第二个式子xk是在第k帧图像捕获到的IMU状态，包括位置，速度，旋转（PVQ）和加速度偏置，陀螺仪偏置。第三个式子是相机外参。注意：xk只与IMU项和Marg有关；特征点深度也只与camera和Marg有关；

2、目标函数为：

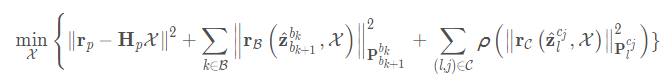
视觉惯性BA：这三项分别为边缘化的先验信息、IMU的测量残差、视觉的重投影误差

BA优化模型分为三部分：

1、Marg边缘化残差部分（滑动窗口中去掉位姿和特征点约束）代码中使用Google开源的Ceres solver解决。

2、IMU残差部分（滑动窗口中相邻帧间的IMU产生）

3、视觉误差函数部分（滑动窗口中特征点在相机下视觉重投影残差）

二、视觉约束

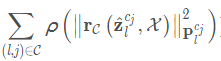
这部分要拟合的目标可以通过重投影误差约束，求解的是对同一个路标点的观测值和估计值之间的误差，注意是在归一化平面上表示。（视觉测量残差就是重投影误差，定义为一个特征点在归一化相机坐标系下的估计值与观测值的差。估计值即特征点的三维空间坐标(x,y,z)^T ，观测值为其在相机归一化平面的坐标。）

1.视觉重投影误差residual（归一化平面）

相关自变量是：该路标点被两帧观察到的相机帧位姿、Cam和IMU之间相对位姿、路标点在第一帧的逆深度。

当某路标点在第i帧观测到并进行初始化操作得到路标点逆深度，当其在第j帧也被观测到时，估计其在第j帧中的坐标为：

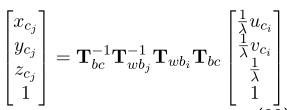
此时的视觉残差为：（左侧为根据i帧反推估计的位置，右侧为观测值）

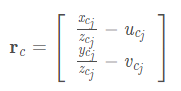
逆深度参数化

逆深度作为参数原因：1）观测到的特征点深度可能非常大，难以进行优化；2）可以减少实际优化的参数变量；3）逆深度更加服从高斯分布。这里特征点的逆深度在第i帧初始化操作中得到。

以上是对针孔相机模型的视觉残差，而在VINS论文中其实显示的是对一般相机模型的视觉残差，即使用了广角相机的球面模型。用的是单位半球体的相机观测残差。是一个鱼眼相机。

在相机的归一化平面上比较残差，再将视觉残差投影到单位球面的正切平面上。由于视觉残差的自由度是2，所以我们将残差向量投影到切平面上。（这里将重投影和测量值都归一化为单位向量，将视觉残差为两个单位向量的差。因为视觉残差的自由度为2，再将视觉残差投影到正切平面上，b1b2为正切平面的两个正交基。）
在第i帧第一次观测到第l个路标点，在第j帧中对该路标点进行观测的残差为：
第一个式子就是残差的表达式，第二个式子是鱼眼相机反投影函数将观测到的像素坐标转换成单位向量的观测值数据，b1和b2是此单位向量的切平面上的一组基。第三个式子是重投影估计模型。其实VINS代码中也可以使用普通的针孔相机模型。

2、优化变量
包括两个时刻的状态量、外参，以及逆深度。

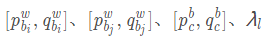
值得注意的是：和纯视觉不同的是，待优化的状态量中的旋转平移都是IMU系到w系，而不是Camera到w系。

状态量特征：

1、待优化量和IMU约束中待优化量有重叠，再次体现了紧耦合。

2、和IMU不同的是，IMU每次优化的状态量是相邻两帧的，但是视觉优化的2帧不一定是相邻的，因此用i，j表示。

3、Jacobian
这里我们采用针孔相机的（归一化相机平面）视觉残差来进行推导，而相机球面模型的视觉残差推导过程也相似。

求解Jacobian就是用视觉残差对上述7个状态变量进行求导。

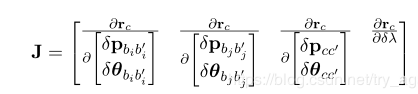
方法一：崔博直接给出答案

2）

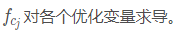
这一部分的具体代码实现在projection_factor.cpp 的 bool ProjectionFactor::Evaluate() 函数中，由于数学公式很容易找到对应，这里就不对代码做解释了。

方法二：深蓝学院详细推导

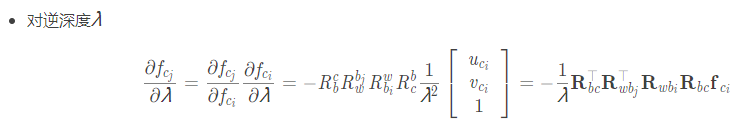4、协方差
视觉约束的协方差与标定相机内参时的重投影误差有关。VINS在代码中sqrt_info取1.5个像素，对应到归一化相机平面还需除以焦距f，最后得到的信息矩阵：（这里真正的信息矩阵其实是sqrt_info的平方）

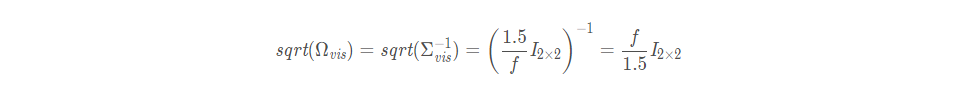
void Estimator::setParameter()
{for (int i = 0; i < NUM_OF_CAM; i++){tic[i] = TIC[i];ric[i] = RIC[i];}f_manager.setRic(ric);ProjectionFactor::sqrt_info = FOCAL_LENGTH / 1.5 * Matrix2d::Identity();ProjectionTdFactor::sqrt_info = FOCAL_LENGTH / 1.5 * Matrix2d::Identity();td = TD;
}

三、IMU约束（粗略，祥细见之前）

1、残差：
状态量传播预测与IMU预积分的残差。

2、优化变量：
IMU的第i、j时刻下的p位置，v速度，Q旋转（PVQ），两个偏置ba,bw

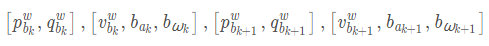
之前对IMU预积分进行了详细讲解。参考：VINS-MONO代码解读—processIMU()+intergrationBase类+imu_factor.h

3、IMU测量残差公式推导
简单来说，如果每一帧IMU都要相对于第一帧求位姿，计算量很大；考虑将PVQ积分公式改为相对第i时刻的姿态。

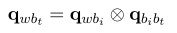
原PVQ积分公式：

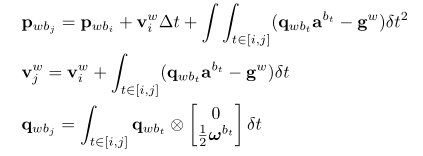
基于预积分的PVQ积分公式

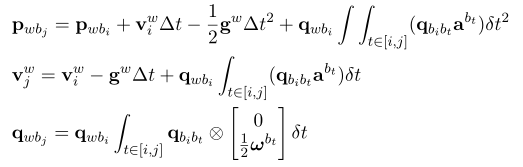
预积分量为：

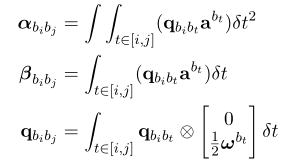
最新的PVQ积分公式变为：

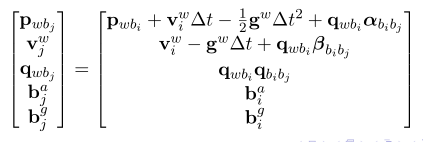
IMU测量残差e为：

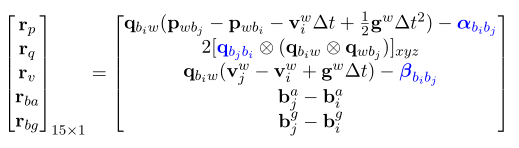
因此其IMU的残差可以写成：

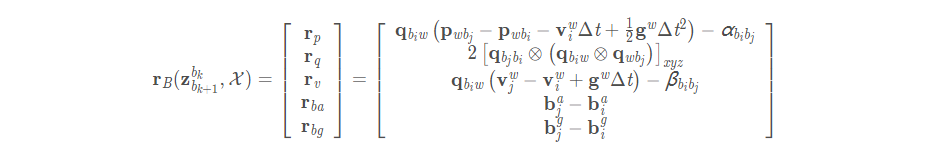
4、残差对状态量的Jacobian
这里直接给出结果，如果想看详细推导，参考：VINS-MONO代码解读—processIMU()+intergrationBase类+imu_factor.h

对应位置补充上这个J的矩阵块就行了，其他位置还是0。一共分为四大模块：


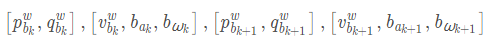
5、残差对状态量的协方差

四、基于舒尔补的边缘化

为什么进行边缘化操作？
如果仅仅从前后两帧图像计算相机位姿，速度快但是精度低；但是采用全局优化BA，连接所有图像帧，精度高但是复杂度高。

采用滑动窗，固定数量的帧进行优化，这样能够保证精度和速度。既然是滑动窗，在滑动的过程中会有新的图像进来，旧的图像离开，所谓边缘化就是为了删除图像，但是把图像信息约束保留下来。

1、论文部分

为了防止pose和特征的个数的复杂度随着时间不断增长，引入边缘化，在移除位姿时将关联的约束转化为先验放入优化问题中。

为了限制基于优化的VIO计算复杂度，引入边缘化。有选择地从滑动窗口中将IMU状态xK和特征λ1边缘化，同时将对应于边缘状态的测量值转换为先验。

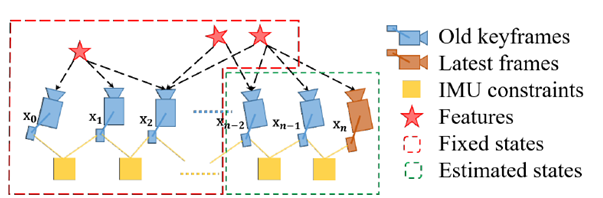
分为两种情况，1、一种是倒数第二帧如果是关键帧的话，将最旧的pose移出Sliding Window，
将最旧帧关联的视觉和惯性数据边缘化掉。把第一个老关键帧及其测量值被边缘化；
Margin_Old作为先验值。2、如果倒数第二帧不是关键帧的话，那么就只剔除倒数第二帧的视觉观测，而不剔除它的IMU约束。
原因是边缘化保证关键帧之间有足够视差而能够三角化足够多的地图点。并且保证了IMU预积分的连贯性。

为了保持系统的稀疏性，我们不会边缘化非关键帧的所有测量值。

2、基本公式
我们根据运动模型和观测模型建立H矩阵（高斯牛顿法中的JJT）的过程其实就是根据概率图模型（多元高斯分布）建立各个节点变量间的信息矩阵（协方差矩阵的逆）的过程，而边缘化则是去掉概率图中的某一个节点后信息矩阵会发生怎样的变换的问题。

基于高斯牛顿的非线性优化理论可知，H*delta_x=b可以写成：

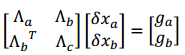
其中，delta_xa和delta_xb分别是希望marg掉的部分和保留部分。

VINS中需要边缘化滑动窗口中的最老帧，目的是希望不再计算这一帧的位姿或者与其相关的路标点，但是希望保留该帧对窗口内其余帧的约束关系。我们基于与移除状态相关的所有边缘化测量值构造一个先验。新的先验项被添加到现有的先验项中。

3、舒尔补
4、marg后形成的先验

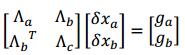
xa为需要marg的变量，假设为相机pose,我们更关心如何求解希望保留的xb，而不再求解xa（即marg的变量改为0，左乘时左上是0），这里是要变化为上三角。

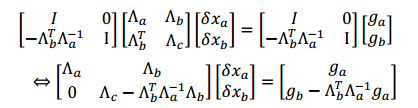
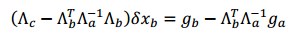
即：new_H*delta_xb=new_b;

形成新的信息矩阵new_H具体流程：
注意：去掉了x1,但是之前和x1相连的所有量x2 x3 x4 x5 在marg掉x1后变得两两相连。

5 具体例子
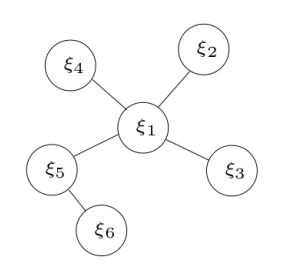
5.1 原来的信息矩阵H的构成

上述最小二乘问题，对用的高斯牛顿求解为：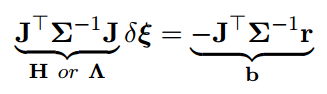
矩阵乘法公式写成连加：

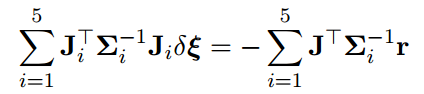
雅克比J和信息矩阵H的稀疏性：由于每个残差只和某几个状态量有关，因此，雅克比矩阵求导时，无关项的雅克比为 0。
将五个残差的信息矩阵加起来，得到样例最终的信息矩阵 Λ, 可视化如下：
5.2 舒尔补后形成新的信息矩阵new_H,并构造为先验

5.3 新测量信息和先验构成新的系统