本文主要是介绍【DL经典回顾】激活函数大汇总(十一)(Tanh Shrink Threshold附代码和详细公式),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
激活函数大汇总(十一)(Tanh Shrink & Threshold附代码和详细公式)
更多激活函数见激活函数大汇总列表
一、引言
欢迎来到我们深入探索神经网络核心组成部分——激活函数的系列博客。在人工智能的世界里,激活函数扮演着不可或缺的角色,它们决定着神经元的输出,并且影响着网络的学习能力与表现力。鉴于激活函数的重要性和多样性,我们将通过几篇文章的形式,本篇详细介绍两种激活函数,旨在帮助读者深入了解各种激活函数的特点、应用场景及其对模型性能的影响。
在接下来的文章中,我们将逐一探讨各种激活函数,从经典到最新的研究成果。
限于笔者水平,对于本博客存在的纰漏和错误,欢迎大家留言指正,我将不断更新。
二、Tanh Shrink
Tanh Shrink激活函数是一种结合了双曲正切函数(Tanh)和Shrinkage思想的激活函数。它在某些深度学习模型中用于处理和转换数据,尤其是在需要强调数据的非线性特征和进行稀疏编码时。
1. 数学定义
Tanh Shrink激活函数的数学表达式定义为:
TanhShrink ( x ) = x − tanh ( x ) \operatorname{TanhShrink}(x)=x-\tanh (x) TanhShrink(x)=x−tanh(x)
其中, x x x是函数的输入。这个函数实际上是输入 x x x减去它的双曲正切值 tanh ( x ) \tanh (x) tanh(x)。
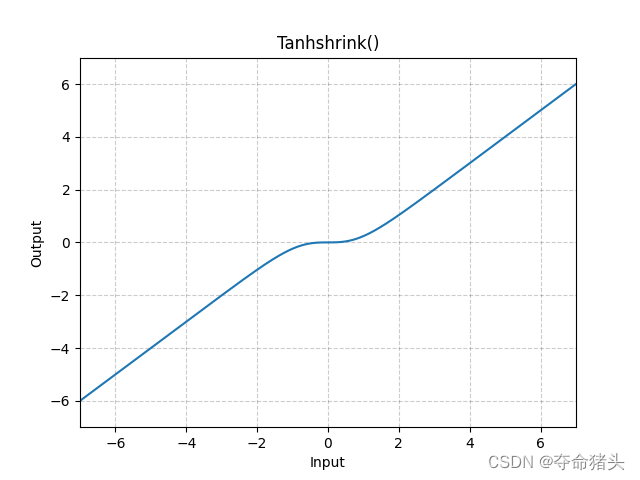
2. 函数特性
- 非线性:Tanh Shrink保持了Tanh函数的非线性特性,使得它可以有效地处理和转换输入数据。
- 输出范围:与Tanh函数不同,Tanh Shrink的输出范围不是固定的。其值取决于输入 x x x与 tanh ( x ) \tanh (x) tanh(x)之间的差异。
- 自正则化性质:通过从输入值中减去其双曲正切值,Tanh Shrink在一定程度上实现了自正则化,有助于模型抵抗过拟合。
3. 导数
Tanh Shrink函数的导数相对简单,可以表示为:
d d x TanhShrink ( x ) = 1 − tanh 2 ( x ) \frac{d}{d x} \operatorname{TanhShrink}(x)=1-\tanh ^2(x) dxdTanhShrink(x)=1−tanh2(x)
这个导数表明,Tanh Shrink函数在任意点 x x x处的梯度取决于 tanh ( x ) \tanh (x) tanh(x)的平方。
4. 使用场景与局限性
使用场景:
- 稀疏编码:在需要稀疏表示输入数据的应用中,如自编码器和某些压缩算法。
- 去噪和特征提取:在图像处理和信号处理领域,Tanh Shrink可以帮助模型去除噪声并更好地捕获数据的关键特征。
局限性:
- 计算复杂度:与简单的激活函数(如ReLU)相比,Tanh Shrink需要额外的计算步骤(计算 tanh ( x ) \tanh (x) tanh(x)),这可能会增加整体的计算成本。
- 梯度消失问题:虽然Tanh Shrink有自正则化的特性,但它仍然可能面临Tanh函数本身的梯度消失问题,尤其是当输入的绝对值非常大时。
5.代码实现
实现Tanh Shrink激活函数的Python代码可以利用NumPy库,这个库为进行数组和数学运算提供了强大的支持。下面是一个简单的Tanh Shrink函数实现及其解读:
import numpy as npdef tanh_shrink(x):"""计算Tanh Shrink激活函数的值。参数:x -- 输入值,可以是一个数值、NumPy数组或者多维数组。返回:Tanh Shrink激活后的结果。"""return x - np.tanh(x)
解读
- 双曲正切计算:
np.tanh(x)计算了输入x的双曲正切值。这是Tanh Shrink函数核心的一步,因为它提供了输入值的非线性变换。 - 减去双曲正切值:通过从原始输入
x中减去其双曲正切值,实现了Tanh Shrink激活函数的定义。这种操作有助于调节输入值,尤其是对于较大或较小的输入值,可以在一定程度上抑制其影响,从而促进模型输出的稀疏性。 - 向量化操作:这个实现通过使用NumPy自然地支持向量化操作,这意味着
tanh_shrink函数可以直接作用于整个数组,无需显式地循环遍历数组中的每个元素。这对于处理大规模数据集非常有用,能显著提高计算效率。
示例使用
以下是如何使用定义的tanh_shrink函数来计算一组输入值的Tanh Shrink激活:
x = np.array([-2, -1, 0, 1, 2])
tanh_shrink_values = tanh_shrink(x)print("Tanh Shrink Values:", tanh_shrink_values)
这段代码展示了对数组x应用Tanh Shrink函数的结果。
三、Threshold
Threshold激活函数是一种在深度学习模型中较少使用的激活函数,其核心思想是对输入值施加一个固定阈值,输入值超过这个阈值时才会被激活。这种激活函数在某些特定场景下可能有用,尤其是在需要明确激活和非激活状态的模型中。
1. 数学定义
Threshold激活函数可以定义为:
Threshold ( x ) = { 1 if x > θ 0 otherwise \text { Threshold }(x)= \begin{cases}1 & \text { if } x>\theta \\ 0 & \text { otherwise }\end{cases} Threshold (x)={10 if x>θ otherwise
其中, x x x是函数的输入, θ \theta θ是预设的阈值。

2. 函数特性
- 二值输出:Threshold函数将输出限制为0或1,这使得其输出非常明确,要么是完全激活,要么是完全不激活。
- 简单性:这个激活函数非常简单,计算代价低。
- 非连续性:Threshold函数在阈值 θ \theta θ处是非连续的,这可能会导致训练过程中的梯度问题。
3. 导数
Threshold函数的一个主要缺点是它在大部分点上的导数为0,在阈值处导数未定义。这意味着它不能直接用于基于梯度的优化方法,如反向传播,因为它不会对输入的微小变化做出反应。
4. 使用场景与局限性
使用场景:
- 二分类问题:在一些特定的二分类问题中,Threshold函数可以作为输出层的激活函数,直接产生二分类结果。
- 特征选择:在预处理步骤或网络的某一层中,Threshold激活可以用于特征选择,即只让重要的信号通过。
局限性:
- 训练困难:由于其非连续性和导数的特性,使用Threshold激活函数的网络难以通过传统的基于梯度的方法进行训练。
- 灵活性有限:Threshold函数提供的是硬性的决策边界,这在处理复杂或模糊的分类问题时可能不够灵活或有效。
尽管Threshold激活函数在理论上简单明了,但在实际深度学习应用中,其使用受到了较大限制,主要因为它不适合梯度下降等常用的优化算法。在选择使用Threshold函数时,需要仔细考虑模型的需求和训练方法。
5.代码实现
import numpy as npdef threshold_activation(x, theta=0.0):"""计算Threshold激活函数的值。参数:x -- 输入值,可以是一个数值、NumPy数组或者多维数组。theta -- 阈值,默认为0.0。返回:根据Threshold激活函数计算得到的结果。"""return (x > theta).astype(float)
解读
- 阈值判断:这个函数通过比较输入
x与阈值theta,来决定输出是0还是1。当x大于theta时,输出1;否则输出0。 - 类型转换:使用
.astype(float)将布尔数组转换为浮点数数组,以便于与深度学习框架和数学运算兼容。 - 向量化操作:该实现利用了NumPy的向量化操作,使得函数可以高效地同时处理多个输入值,无需显式循环。
示例使用
x = np.array([-1, 0, 0.5, 1])
threshold_values = threshold_activation(x, theta=0.5)print("Threshold Activation Values:", threshold_values)
这段代码展示了如何对一个数组x应用Threshold激活函数,其中阈值theta被设定为0.5。
四、参考文献
对于Tanh Shrink和Threshold函数的直接文献引用可能较少,因为它们不像某些激活函数那样在深度学习社区中广泛使用。然而,它们的概念和应用可以在更广泛的深度学习、信号处理和神经网络优化的文献中找到间接的讨论。特别是,它们在讨论网络的稀疏性、正则化策略以及早期神经网络模型的设计和分析时可能会被提及。
这篇关于【DL经典回顾】激活函数大汇总(十一)(Tanh Shrink Threshold附代码和详细公式)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




