算法时空复杂度分析：大O表示法

本文主要是介绍算法时空复杂度分析：大O表示法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言

算法题写完以后，面试官经常会追问一下你这个算法的时空复杂度是多少？（好像作为一名算法工程师，我日常码代码的过程中，并没有太注意这个，惭愧～但是找做后端开发的男票求证了一下，他们日常工作确实会去考虑这种问题）那么无论是为了应付面试，还是为了未来码代码可以精益求精，都还是认真的学一下时空复杂度分析方法吧！

对于为什么需要时空复杂度分析，而不是直接跑一下代码看看，看到王争大佬在《数据结构与算法之美》（墙推）里给的两个原因是：

1. 测试结果依赖测试环境：机器的配置会十分影响你跑出的结果；
2. 测试结果依赖数据规模的大小。

因此，我们需要一个不依赖数据规模和测试环境，帮助粗略估计算法执行效率的方法！也就是下面的大O表示法～

大O表示法

举个栗子🌰，下面这个函数的总的执行时间$T(n)=1+2n$个unit time！

def f(n: int)a = 0  # 1个unit timefor i in range(n):  # n个unit timea += i  # n个unit timereturn a

再举个栗子🌰，下面这个函数的总的执行时间$T(n)=1+n+2n^2$个unit time！

def g(n: int, m: int)a = 0  # 1个unit timefor i in range(n):  # n个unit timefor j in range(n): # n^2个unit timea += i*j  # n^2个unit timereturn a

用一个公式表示就是：

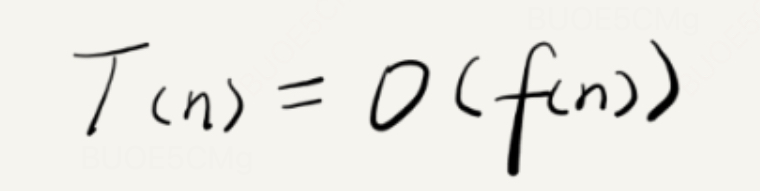
其中：

• $T(n)$表示代码执行的时间；
• $n$：表示数据规模的大小；
• $f(n)$：表示每行代码执行的次数总和
• $O$：表示执行时间$T(n)$与$f(n)$成正比。

所以第一个例子的时间复杂度为$T(n)=1+2n$，第二个例子的时间复杂度为$T(n)=1+n+2n^2$，这就是大O时间复杂度表示法。大O时间复杂度表示法实际上并不是具体值代码执行的时间，而是代表代码执行时间随着数据规模增长的变化趋势，所以也叫渐进时间复杂度，简称时间复杂度。

当n很大时，公式中的低阶、常量、系数三部分并不左右增长趋势，所以都可以忽略，只需要记录一个最大量级即可！因此，上例的时间复杂度可以记为：$T(n)=O(n)$、$T(n)=O(n^2)$。

3个时间复杂度分析原则

3个原则：

1. 只关注循环执行次数最多的一段代码：
还是上面第一个例子，关注for循环这段代码就行了，a = 0这类代码都是常量级的执行时间，与$n$无关。

def f(n: int)a = 0  # 1个unit timefor i in range(n):  # n个unit timea += i  # n个unit timereturn a

2. 总复杂度 = 量级最大的那段代码的复杂度：
这个有点像运筹学里关键路径法的思想，只有找到了最关键/量级最大的，你去优化的时候才能发力在刀刃上～

比如下面这段代码，有一层for循环的，有两层for循环，我们去关注两层for循环的这段代码即可。

def g(n: int, m: int)for i in range(n):passa = 0  # 1个unit timefor i in range(n):  # n个unit timefor j in range(n): # n^2个unit timea += i*j  # n^2个unit timereturn a

3. 嵌套代码的复杂度 = 嵌套内外代码复杂度的乘积：
上面的第二个例子，两层for循环嵌套，最后的时间复杂度 = 外层for循环的复杂度乘以里面for循环的复杂度。

def g(n: int, m: int)a = 0  # 1个unit timefor i in range(n):  # n个unit timefor j in range(n): # n^2个unit timea += i*j  # n^2个unit timereturn a

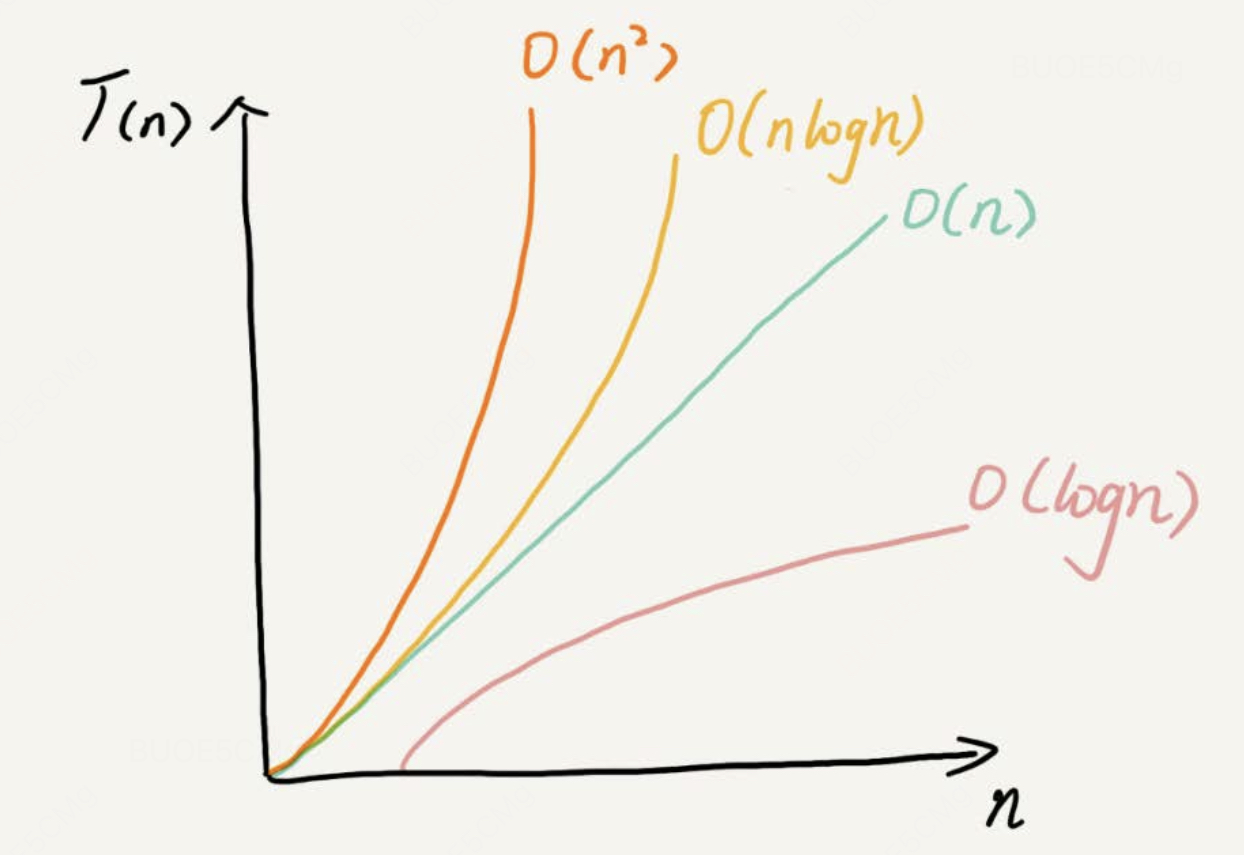
常见的时间复杂度量级

• 多项式量级：下图左侧；
• 非多项式量级：下图右侧波浪线。执行时间会随着数据规模的增大而急剧增大，是非常低效的算法！

空间复杂度

又称为渐进空间复杂度，表示算法的存储空间与数据规模之间的增长关系！

举个栗子🌰，空间复杂度为$O(n)$

def f(n: int):a = 2  # 1个空间存储变量，常量b = [] # 从下面代码可以看出时一个大小为n的数组for i in range(n):b.append(i)return b

参考资料

1. 《数据结构与算法之美》王争

这篇关于算法时空复杂度分析：大O表示法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---