第四章 OpenGL ES 基础-位移、缩放、旋转原理

本文主要是介绍第四章 OpenGL ES 基础-位移、缩放、旋转原理，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

第四章 OpenGL ES 基础-位移、缩放、旋转原理

第一章 OpenGL ES 基础-屏幕、纹理、顶点坐标
第二章 OpenGL ES 基础-GLSL语法简单总结
第三章 OpenGL ES 基础-GLSL渲染纹理
第四章 OpenGL ES 基础-位移、缩放、旋转原理
第五章 OpenGL ES 基础-透视投影矩阵与正交投影矩阵
第六章 OpenGL ES 基础-FBO、VBO理解与运用
第七章 OpenGL ES 基础-输入输出框架思维

矩阵小知识

对应矩阵效果
注意:必须是相同维度矩阵才行,比如23矩阵不能和33矩阵进行加减
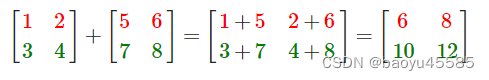
在这里插入图片描述
矩阵与标量数乘和矩阵与标量加减类似, 实际是对矩阵的每个元素和该标量进行相乘,如下图所示
所以值其实就是两个矩阵行列式相乘的和,取出矩阵A的i行下的所有元素与矩阵B的j列下的所有元素进行相乘和
在这里插入图片描述

OpenGL 初始化矩阵原理

并且任何矩阵与单位矩阵相乘都为矩阵本身.如下图所示:
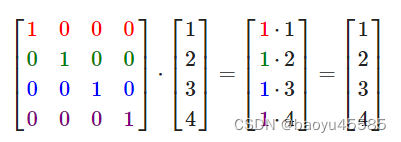
在这里插入图片描述

根据上图的原理你可以4*4的矩阵，可以默认初始化矩阵，如下代码

void m3dLoadIdentity44(M3DMatrix44f m)
{// Don't be fooled, this is still column majorstatic M3DMatrix44f     identity = { 1.0f, 0.0f, 0.0f, 0.0f,0.0f, 1.0f, 0.0f, 0.0f,0.0f, 0.0f, 1.0f, 0.0f,0.0f, 0.0f, 0.0f, 1.0f };memcpy(m, identity, sizeof(M3DMatrix44f));
}

OpenGL的XYZ位移矩阵原理

在4×4矩阵上有几个特别的位置用来执行特定的操作，对于位移来说它们是第四列最上面的3个值。如果我们把位移向量表示为(Tx,Ty,Tz)，我们就能把位移矩阵定义为：
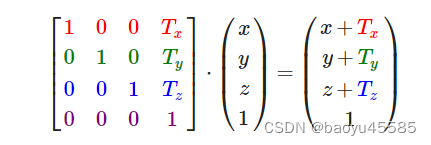
在这里插入图片描述
m3dLoadIdentity44初始化后，对Tx,Ty,Tz进行对应参数补充

void m3dTranslationMatrix44(M3DMatrix44f m, float x, float y, float z)
{// 初始化为单位矩阵m3dLoadIdentity44(m);// 填充位移矩阵的最后一列m[12] = x;m[13] = y;m[14] = z;
}

OpenGL的缩放矩阵原理

矩阵来实现缩放功能, 如果我们把缩放变量表示为(S1,S2,S3)我们可以为任意向量(x,y,z)定义一个缩放矩阵：S1=2,x就放大2倍
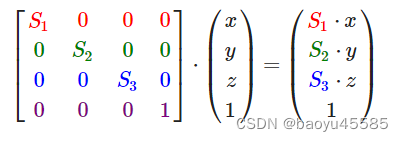
在这里插入图片描述
所以上面图可以推测下标0，5，10的位置进行数据填充

void m3dScaleMatrix44(M3DMatrix44f m, float xScale, float yScale, float zScale)
{// 初始化为单位矩阵m3dLoadIdentity44(m);// 填充缩放矩阵的对角线元素m[0] = xScale;m[5] = yScale;m[10] = zScale;
}

OpenGL的旋转矩阵原理

对向量进行旋转也是通过矩阵实现.

比如对于二维进行旋转,其本质就是将z轴作为旋转轴实现旋转,

比如下图所示,由向量v向右旋转θ角度得到向量k:
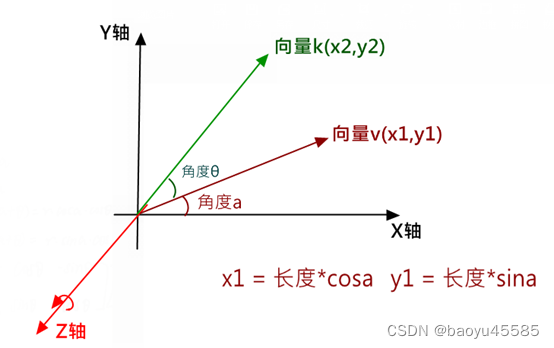
在这里插入图片描述
那么我们如何获取向量k的x2和y2呢?
由于两个向量的长度都是相同的.并且:

x1 = 长度cosa y1 = 长度sina

所以:

x2 = 长度cos(a+θ) = 长度cosacosθ – 长度sinasinθ= x1cosθ – y1*sinθ

y2 =长度sin(a+θ) = 长度sinacosθ + 长度cosasinθ = y1cosθ + x1*sinθ

所以沿Z轴旋转的矩阵等于:
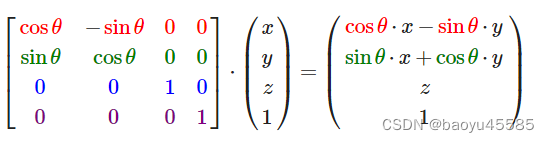
在这里插入图片描述
同理得出沿x轴旋转为:

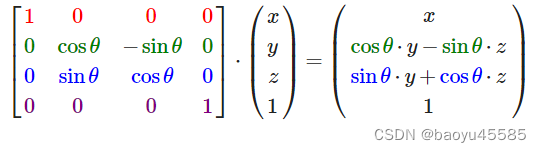
沿y轴旋转为:

利用旋转矩阵我们可以把任意位置向量沿一个单位旋转轴进行旋转。也可以将多个矩阵复合，比如先沿着x轴旋转再沿着y轴旋转。但是这会很快导致一个问题——万向节死锁（Gimbal Lock）。在这里我们不会讨论它的细节，但是对于3D空间中的旋转，一个更好的模型是沿着任意的一个轴，比如单位向量(0.662, 0.2, 0.7222)旋转，而不是对一系列旋转矩阵进行复合。这样的一个（超级麻烦的）矩阵是存在的，见下面这个公式，其中(Rx,Ry,Rz)代表任意旋转轴：
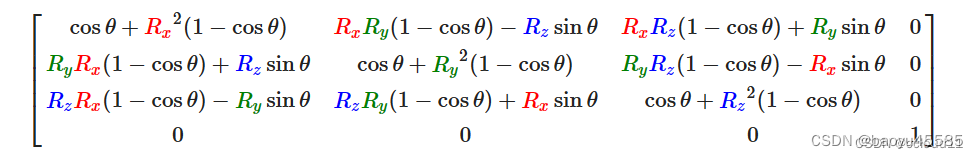
在这里插入图片描述

有上面三个矩阵推测出

void m3dRotationMatrix44(M3DMatrix44f m, float angle, float x, float y, float z)
{float c = cos(angle);float s = sin(angle);float t = 1.0f - c;// 归一化旋转轴float mag = sqrt(x*x + y*y + z*z);if (mag > 0.0f) {x /= mag;y /= mag;z /= mag;} else {// 如果传入的旋转轴为零向量，则返回单位矩阵m3dLoadIdentity44(m);return;}// 填充旋转矩阵m[0] = x*x*t + c;m[1] = y*x*t - z*s;m[2] = z*x*t + y*s;m[3] = 0.0f;m[4] = x*y*t + z*s;m[5] = y*y*t + c;m[6] = z*y*t - x*s;m[7] = 0.0f;m[8] = x*z*t - y*s;m[9] = y*z*t + x*s;m[10] = z*z*t + c;m[11] = 0.0f;m[12] = 0.0f;m[13] = 0.0f;m[14] = 0.0f;m[15] = 1.0f;
}