Wilson威尔逊平滑

2024-03-11 23:36

文章标签 平滑威尔逊 wilson

本文主要是介绍Wilson威尔逊平滑，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1、威尔逊平滑引入的动机

在曝光很少的情况下，计算出的CTR并不真实可靠，而样本数越大，CTR的比例才越准确，更能反应真实情况。

为了衡量样本数对于CTR信区间的影响，我们引入"威尔逊（Wilson）区间"的概念。Wilson区间的含义就是，就是指在一定置信度下，真实的CTR范围是多少。

2、威尔逊平滑公式

p —— 概率，即点击的概率，也就是 CTR

n —— 样本总数，即曝光数

z —— 在正态分布里，均值 + z * 标准差会有一定的置信度。例如 z 取 1.96，就有 95% 的置信度。

Wilson区间的含义就是，就是指在一定置信度下，真实的 CTR 范围是多少。

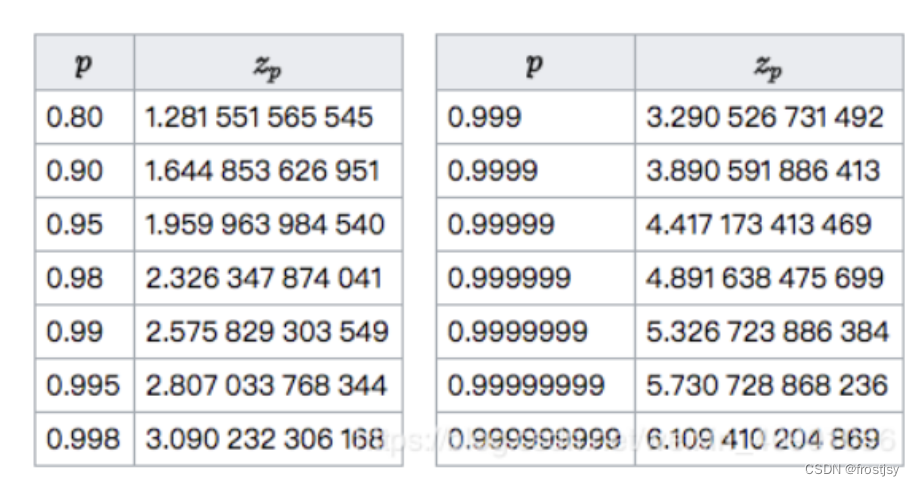
3、置信度区间z参数设置

置信度水平与区间的关系如下

4、威尔逊几种实现代码

设置n小于多少时，认定为小样本，下面默认曝光次数小于10000时为小样本。

class WilsonCorrect(object):def evaluate(self, p, n, z=1.96, threshold=10000):score = pp = min(p, 1)if 0 < n < threshold:try:score = (p + z * z / (2 * n) - z / (2 * n) * math.sqrt(4 * n * (1 - p) * p + z * z)) / (1 + z * z / n)except:passreturn score

当ctr大于某一阈值时，直接归0

import numpy as npdef walson_ctr(num_click, num_pv, z=1.96):p = num_click * 1.0 / num_pvif p > 0.9:return 0.0n = num_pvA = p + z**2 / (2*n)B = np.sqrt(p * (1-p) / n + z**2 / (4*(n**2)))C = z * BD = 1 + z**2 / nctr = (A - C) / Dreturn ctr

全走wilson平滑

double walson_ctr(int num_pv, int num_click) {if (num_pv * num_click == 0 || num_pv < num_click) {return 0.f;}double score = 0.f;double z = 1.96f;int n = num_pv;double p = 1.0f * num_click / num_pv;score = (p + z*z/(2.f*n) - z*sqrt((p*(1.0f - p) + z*z /(4.f*n))/n)) / (1.f + z*z/n);return score;
}