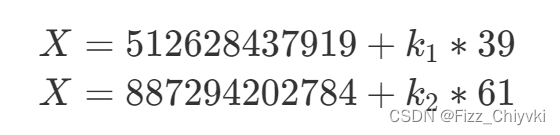原题目： 题目大意：1e12的阶乘，不算末尾的0，后5位数字为多少 解题思路： 暴力运算也能算，就是有点慢，优化过后可能也得算个几十分钟 这里考虑使用威尔逊定理+费马小定理 用这个方法我们就可以得到对于任何一个小于p的数n，p为素数，n！在模p下的结果， 对于本题： 则我们要找的答案应该是512628437919+k*39的最后几位有效数字，当k＞100000时，显然末尾数字就

1、威尔逊平滑引入的动机 在曝光很少的情况下，计算出的CTR并不真实可靠，而样本数越大，CTR的比例才越准确，更能反应真实情况。 为了衡量样本数对于CTR信区间的影响，我们引入"威尔逊（Wilson）区间"的概念。Wilson区间的含义就是，就是指在一定置信度下，真实的CTR范围是多少。 2、威尔逊平滑公式 p —— 概率，即点击的概率，也就是 CTR  n —— 样本总数，即曝光数

https://www.deeplearn.me/2362.html 出，无论得分情况为 得分 = 赞成票 – 反对票 还是 得分 = 赞成票 ／ 全部票 都会出现错误的情况。 有一种计算得分的策略是，通过某事件发生的概率的最低置信区间来对项目进行排序。 所谓”置信区间”，就是说，以某个概率而言，p会落在的那个区间。比如，某个产品的好评率是80%，但是这个值不一定可信。根据统计学，我们只

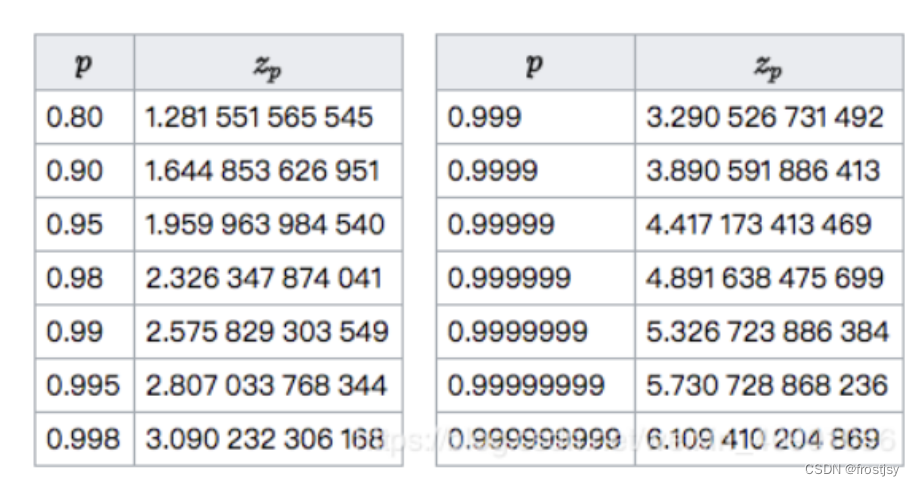
迄今为止，这个系列都在讨论，如何给出"某个时段"的排名，比如"过去24小时最热门的文章"。 但是，很多场合需要的是"所有时段"的排名，比如"最受用户好评的产品"。 这时，时间因素就不需要考虑了。这个系列的最后两篇，就研究不考虑时间因素的情况下，如何给出排名。 一种常见的错误算法是： 　　得分 = 赞成票 - 反对票 假定有两个项目，项目A是60张赞成票，40张反对票，项