（数据结构）如何手搓一棵伸展树（splay tree）

2024-03-11 22:40
文章标签 数据结构 tree splay 伸展 一棵

本文主要是介绍（数据结构）如何手搓一棵伸展树（splay tree），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

伸展树作为BST的又一个派生类

其主要特色是没每插入或查找一个节点，会把该节点通过一次次的旋转伸展至树根，并且减少树高

使得用户经过一段时间的使用后

高访问频率的数据集中在树根位置，查询深度浅，速度快

从而达到提高效率的目的

因此相较而言，AVL树更像是循规蹈矩，如履薄冰。而伸展树则更加潇洒，不羁小节。

例如一颗这样的伸展树

如果你访问001节点，即访问最底的节点

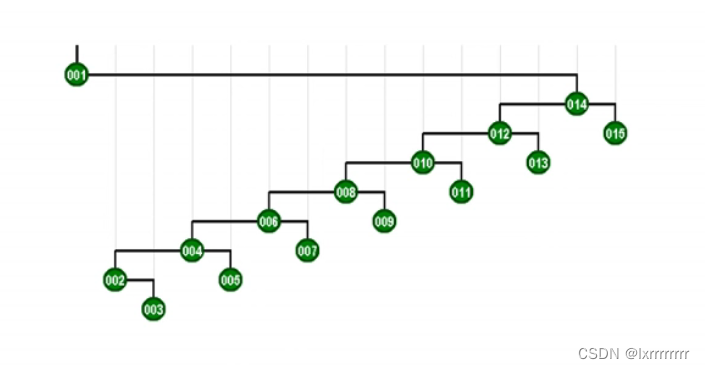
伸展树会把001伸展至根节点，同时缩短书高

在访问一次003节点

树会伸展至如下图结构

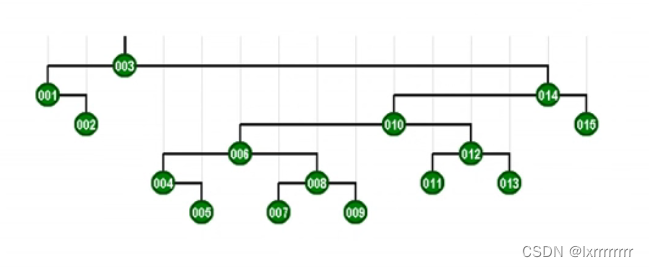
为方便理解，首先介绍几个旋转方式：

zig为顺时针旋转，zag为逆时针旋转，可以看到，经过这种单层旋转

可以将V节点提升一层

而两个单层旋转互相组合，可以有四种双层旋转

分别为zag-zag，zig-zig zig-zag zag-zig四种

其中zig-zig旋转：

zag-zag旋转：

zag-zig旋转

 zig-zag旋转

可以看到以上节点都把V提升了两层

似曾相似对不对

zig-zag和zag-zig就是上篇中平衡AVL树的3+4重构的转法

一会代码也会有所体现

为什么要引入双层旋转：

因为如果全采用单层旋转，那么顺序访问节点后会发现树高没有变，复杂度会飙到n方

类似下图

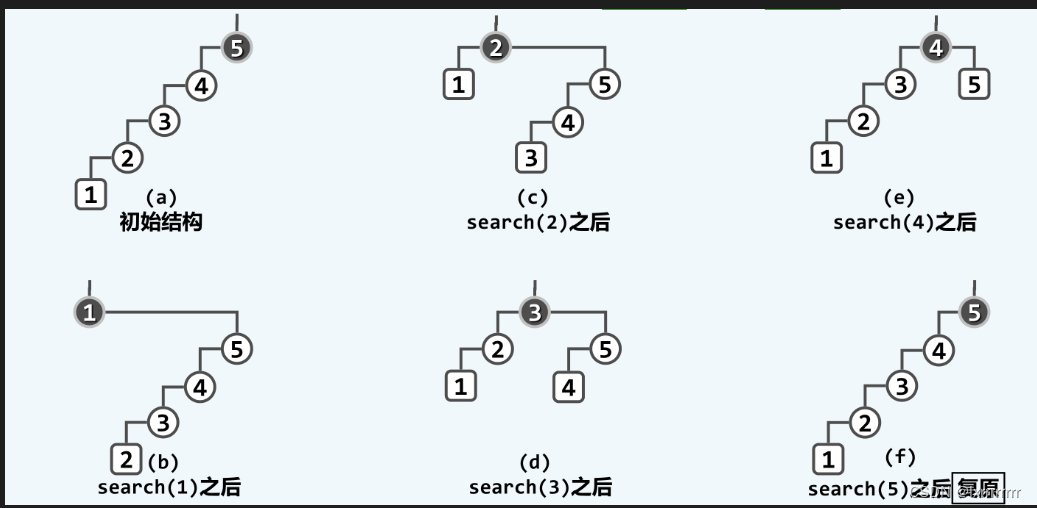
这里就不过多赘述推导过程了，可以去查下相关资料

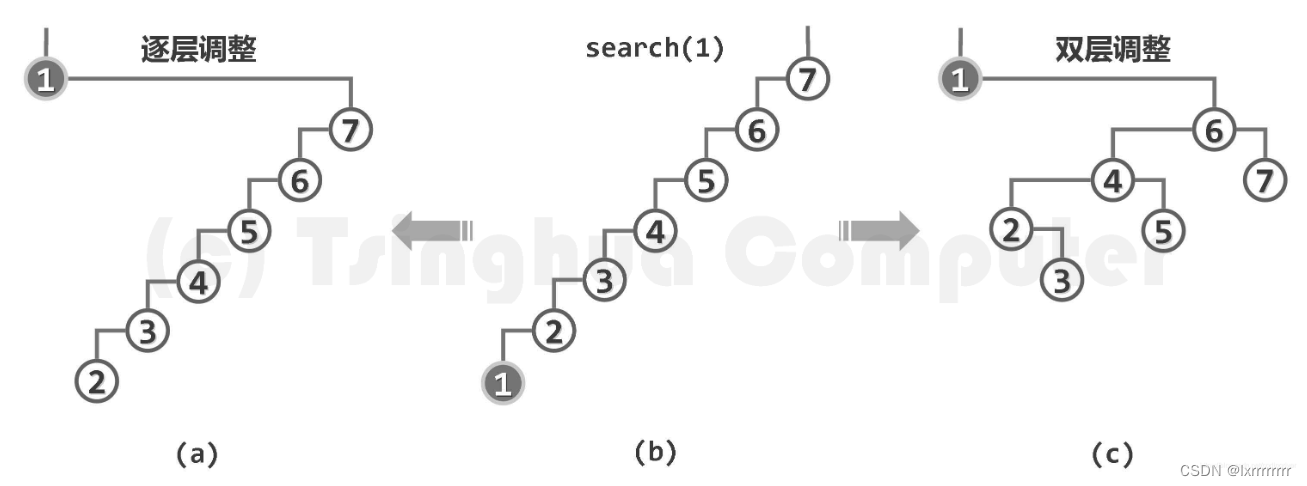
只有双层旋转才可以有效减少树高，提升效率

经过以上分析，我们先把前置的旋转函数写以下

毕竟我们以前的代码是处理不了单旋，zigzig，zagzag这四种情况的

相信对于聪明的你这并不难写

代码如下

旋转

template <typename K,typename V>
lxrbinnodeposi(T) lxrSplayTree<K,V>::zig(lxrbinnodeposi(T) p){lxrbinnodeposi(T) x=p->leftchild;p->leftchild=x->rightchild;if(x->rightchild) x->rightchild->parent=p;x->rightchild=p;p->parent=x;this->updateHeight(p);this->updateHeight(x);return x;
}template <typename K,typename V>
lxrbinnodeposi(T) lxrSplayTree<K,V>::zag(lxrbinnodeposi(T) p){lxrbinnodeposi(T) x=p->rightchild;p->rightchild=x->leftchild;if(x->leftchild) x->leftchild->parent=p;x->leftchild=p;p->parent=x;this->updateHeight(p);this->updateHeight(x);return x;
}template <typename K,typename V>
lxrbinnodeposi(T) lxrSplayTree<K,V>::zigzig(lxrbinnodeposi(T) g){lxrbinnodeposi(T) p=g->leftchild;lxrbinnodeposi(T) x=p->leftchild;p->leftchild=x->rightchild;if(x->rightchild) x->rightchild->parent=p;x->rightchild=p;p->parent=x;g->leftchild=p->rightchild;if(p->rightchild) p->rightchild->parent=g;p->rightchild=g;g->parent=p;this->updateHeight(g);this->updateHeight(p);this->updateHeight(x);return x;
}template <typename K,typename V>
lxrbinnodeposi(T) lxrSplayTree<K,V>::zagzag(lxrbinnodeposi(T) g){lxrbinnodeposi(T) p=g->rightchild;lxrbinnodeposi(T) x=p->rightchild;p->rightchild=x->leftchild;if(x->leftchild) x->leftchild->parent=p;x->leftchild=p;p->parent=x;g->rightchild=p->leftchild;if(p->leftchild) p->leftchild->parent=g;p->leftchild=g;g->parent=p;this->updateHeight(g);this->updateHeight(p);this->updateHeight(x);return x;
}

有了以上基础我们就可以顺理成章写出伸展函数

Spaly

虽然代码看起来有些长，但大多数是分类讨论的内容

如果该节点只有父节点而没有祖父节点，那么只能进行单旋，如果他是左儿子就进行zig旋转

反之进行zag旋转

接下来如果x有祖父节点

那我们看他父节点和祖父节点的关系，他和他父节点的关系

按我们上面分析的关系分成四类

其中双左儿子/双右儿子需要进行我们的zigzig/zagzag旋转

余下两个进行3+4重构

按照此方法一直将x伸展至根节点

别忘了更新根节点和树高

代码如下

template <typename K,typename V>
lxrbinnodeposi(T) lxrSplayTree<K,V>::splay(lxrbinnodeposi(T) x){lxrbinnodeposi(T) p;lxrbinnodeposi(T) g;lxrbinnodeposi(T) hot;while(x!= this->__root){p=x->parent,g=p->parent;if(!g){hot=p->parent;x=(x==p->leftchild ? zig(p) : zag(p));x->parent=hot;if(hot) (p==hot->leftchild) ? hot->leftchild:hot->rightchild=x;}else{if(p==g->leftchild){if(x==p->leftchild){hot     =g->parent;x       =zigzig(g);x->parent=hot;if(hot) (g==hot->leftchild ? hot->leftchild : hot->rightchild)=x;}else{hot     =g->parent;x       =this->connect34(p,x,g,p->leftchild,x->leftchild,x->rightchild,g->rightchild);x->parent=hot;if(hot) g==hot->leftchild ? hot->leftchild : hot->rightchild=x;}}else{if(x==p->leftchild){hot     =g->parent;x       =this->connect34(g,x,p,g->leftchild,x->leftchild,x->rightchild,p->rightchild);x->parent=hot;if(hot) g==hot->leftchild ? hot->leftchild : hot->rightchild=x;}else{hot     =g->parent;x       =zagzag(g);x->parent=hot;if(hot) g==hot->leftchild ? hot->leftchild : hot->rightchild=x;}}}if(!x->parent) this->__root=x;}return x;
}

写完了splay函数，伸展树就已经完成一大半了

剩下只要按照伸展树思想完成查找删除和插入函数即可

search

伸展树的search和BST差不多

只是再经过查找之后

我们要将返回的节点伸展至树根

如果返回的是空节点，那就将他的父节点伸展至树根，即__hot

代码如下

template <typename K,typename V>
lxrbinnodeposi(T)& lxrSplayTree<K,V>::search(K const &key){lxrbinnodeposi(T) x=this->searchIn(this->__root,key,(this->__hot)=nullptr);if(x) splay(x);else if(this->__hot) splay(this->__hot);return this->__root;
}

insert

这里给出一种实现方式

直接调用上面伸展树的搜索算法，这样一次搜索必然会失败，但是此时`__hot`会被移动到根结点。我们可以直接比较待插入value与__hot的value的大小，从而直接将被插入结点插入到根结点。整个过程如下图所示：

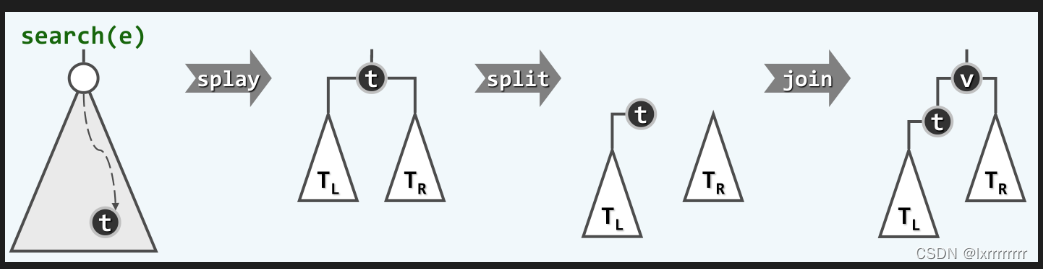
 代码如下：

template <typename K,typename V>
lxrbinnodeposi(T) lxrSplayTree<K,V>::insert(K const &key,V const &value){lxrbinnodeposi(T) x=search(key);if(x&& x->data.key==key) return x;this->__root=new lxrbinnode<T>(entry<K,V>(key,value));++(this->__size);if(!x) return this->__root;if(key < x->data.key){this->__root->leftchild =x->leftchild;this->__root->rightchild=x;x->leftchild            =nullptr;x->parent               =this->__root;}else{this->__root->leftchild  = x;this->__root->rightchild = x->rightchild;x->rightchild            = nullptr;x->parent                = this->__root;}this->updateHeight(x);this->updateHeight((this->__root));return this->__root;
}

 remove

删除函数会比较复杂，这里给出一种实现方式

首先调用伸展树的搜索算法，这样被删除结点就已经被移动到了根结点，因此可以直接将根结点删除。接下来的问题是，应该由哪个结点来作为新的根结点。

在根结点没有左子树或者没有右子树时，可以直接用那棵唯一的子树来替代根结点，从而完成了根结点的删除。但在根结点同时具有左右子树时，根据伸展树的局部性原理，仍可选取被删除结点的直接后继来作为新的根结点，这样数据的局部性仍然可以得到应用。

为了将根结点的直接后继提升为新的根结点，可以在TR中再次查找根结点的关键码，尽管这次查找必然失败，却可以将TR中的最小结点提升为根节点。并且由于它是最小结点，根据BST的局部有序性，新的根节点必然没有左子树，从而可以将TL作为左子树与新的根结点进行连接。这样，就得到了一棵完整的二叉搜索树。整个过程如下图所示：

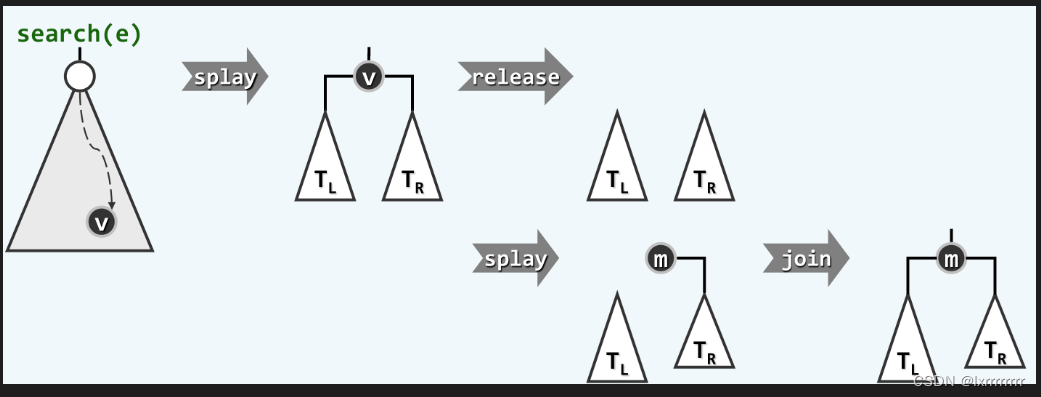
代码如下：

template <typename K,typename V>
bool lxrSplayTree<K,V>::remove(K const &key){lxrbinnodeposi(T) x=search(key);if(!x || x->data.key!=key) return false;if(!(this->__root)->leftchild){this->__root=this->__root->rightchild;if(this->__root) this->__root->parent=nullptr;search(key);}else if(!(this->__root)->rightchild){this->__root=this->__root->leftchild;this->__root->parent=nullptr;search(key);}else{this->__root=x->rightchild;this->__root->parent=nullptr;search(key);                            //move x's succ to root, this->__root->leftchild=x->leftchild;   //and __root has no left child(for succ has the smallest keyx->leftchild->parent=this->__root;this->updateHeight(this->__root);}--(this->__size);delete x;return true;
}

完整代码

#ifndef LXRSPLAYTREE_H_
#define LXRSPLAYTREE_H_#include "../05 BST/lxrBST.h"#define T entry<K,V>
template <typename K,typename V>
class lxrSplayTree:public lxrBST<K,V>{
protected:lxrbinnodeposi(T) splay(lxrbinnodeposi(T) x);lxrbinnodeposi(T) zig(lxrbinnodeposi(T) p);   //right rotationlxrbinnodeposi(T) zag(lxrbinnodeposi(T) p);   //left rotationlxrbinnodeposi(T) zigzig(lxrbinnodeposi(T) g);lxrbinnodeposi(T) zagzag(lxrbinnodeposi(T) g);
public:lxrbinnodeposi(T)& search(K const &key);lxrbinnodeposi(T)  insert(K const &key,V const &value);bool               remove(K const &key);
};//protected methodstemplate <typename K,typename V>
lxrbinnodeposi(T) lxrSplayTree<K,V>::splay(lxrbinnodeposi(T) x){lxrbinnodeposi(T) p;lxrbinnodeposi(T) g;lxrbinnodeposi(T) hot;while(x!= this->__root){p=x->parent,g=p->parent;if(!g){hot=p->parent;x=(x==p->leftchild ? zig(p) : zag(p));x->parent=hot;if(hot) (p==hot->leftchild) ? hot->leftchild:hot->rightchild=x;}else{if(p==g->leftchild){if(x==p->leftchild){hot     =g->parent;x       =zigzig(g);x->parent=hot;if(hot) (g==hot->leftchild ? hot->leftchild : hot->rightchild)=x;}else{hot     =g->parent;x       =this->connect34(p,x,g,p->leftchild,x->leftchild,x->rightchild,g->rightchild);x->parent=hot;if(hot) g==hot->leftchild ? hot->leftchild : hot->rightchild=x;}}else{if(x==p->leftchild){hot     =g->parent;x       =this->connect34(g,x,p,g->leftchild,x->leftchild,x->rightchild,p->rightchild);x->parent=hot;if(hot) g==hot->leftchild ? hot->leftchild : hot->rightchild=x;}else{hot     =g->parent;x       =zagzag(g);x->parent=hot;if(hot) g==hot->leftchild ? hot->leftchild : hot->rightchild=x;}}}if(!x->parent) this->__root=x;}return x;
}template <typename K,typename V>
lxrbinnodeposi(T) lxrSplayTree<K,V>::zig(lxrbinnodeposi(T) p){lxrbinnodeposi(T) x=p->leftchild;p->leftchild=x->rightchild;if(x->rightchild) x->rightchild->parent=p;x->rightchild=p;p->parent=x;this->updateHeight(p);this->updateHeight(x);return x;
}template <typename K,typename V>
lxrbinnodeposi(T) lxrSplayTree<K,V>::zag(lxrbinnodeposi(T) p){lxrbinnodeposi(T) x=p->rightchild;p->rightchild=x->leftchild;if(x->leftchild) x->leftchild->parent=p;x->leftchild=p;p->parent=x;this->updateHeight(p);this->updateHeight(x);return x;
}template <typename K,typename V>
lxrbinnodeposi(T) lxrSplayTree<K,V>::zigzig(lxrbinnodeposi(T) g){lxrbinnodeposi(T) p=g->leftchild;lxrbinnodeposi(T) x=p->leftchild;p->leftchild=x->rightchild;if(x->rightchild) x->rightchild->parent=p;x->rightchild=p;p->parent=x;g->leftchild=p->rightchild;if(p->rightchild) p->rightchild->parent=g;p->rightchild=g;g->parent=p;this->updateHeight(g);this->updateHeight(p);this->updateHeight(x);return x;
}template <typename K,typename V>
lxrbinnodeposi(T) lxrSplayTree<K,V>::zagzag(lxrbinnodeposi(T) g){lxrbinnodeposi(T) p=g->rightchild;lxrbinnodeposi(T) x=p->rightchild;p->rightchild=x->leftchild;if(x->leftchild) x->leftchild->parent=p;x->leftchild=p;p->parent=x;g->rightchild=p->leftchild;if(p->leftchild) p->leftchild->parent=g;p->leftchild=g;g->parent=p;this->updateHeight(g);this->updateHeight(p);this->updateHeight(x);return x;
}//public interfavestemplate <typename K,typename V>
lxrbinnodeposi(T)& lxrSplayTree<K,V>::search(K const &key){lxrbinnodeposi(T) x=this->searchIn(this->__root,key,(this->__hot)=nullptr);if(x) splay(x);else if(this->__hot) splay(this->__hot);return this->__root;
}template <typename K,typename V>
lxrbinnodeposi(T) lxrSplayTree<K,V>::insert(K const &key,V const &value){lxrbinnodeposi(T) x=search(key);if(x&& x->data.key==key) return x;this->__root=new lxrbinnode<T>(entry<K,V>(key,value));++(this->__size);if(!x) return this->__root;if(key < x->data.key){this->__root->leftchild =x->leftchild;this->__root->rightchild=x;x->leftchild            =nullptr;x->parent               =this->__root;}else{this->__root->leftchild  = x;this->__root->rightchild = x->rightchild;x->rightchild            = nullptr;x->parent                = this->__root;}this->updateHeight(x);this->updateHeight((this->__root));return this->__root;
}template <typename K,typename V>
bool lxrSplayTree<K,V>::remove(K const &key){lxrbinnodeposi(T) x=search(key);if(!x || x->data.key!=key) return false;if(!(this->__root)->leftchild){this->__root=this->__root->rightchild;if(this->__root) this->__root->parent=nullptr;search(key);}else if(!(this->__root)->rightchild){this->__root=this->__root->leftchild;this->__root->parent=nullptr;search(key);}else{this->__root=x->rightchild;this->__root->parent=nullptr;search(key);                            //move x's succ to root, this->__root->leftchild=x->leftchild;   //and __root has no left child(for succ has the smallest keyx->leftchild->parent=this->__root;this->updateHeight(this->__root);}--(this->__size);delete x;return true;
}#undef T
#endif

但是伸展树并不能保证单次最坏情况的发生，所以不能适用于对效率非常敏感的场合，例如一些安全装置，应急装置，毕竟谁也不敢当赌怪

这篇关于（数据结构）如何手搓一棵伸展树（splay tree）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/799310。

相关文章

【数据结构】——原来排序算法搞懂这些就行，轻松拿捏

【数据结构】——原来排序算法搞懂这些就行，轻松拿捏

前言：快速排序的实现最重要的是找基准值，下面让我们来了解如何实现找基准值 基准值的注释：在快排的过程中，每一次我们要取一个元素作为枢纽值，以这个数字来将序列划分为两部分。 在此我们采用三数取中法，也就是取左端、中间、右端三个数，然后进行排序，将中间数作为枢纽值。 快速排序实现主框架： //快速排序 void QuickSort(int* arr, int left, int rig
阅读更多...
6.1.数据结构-c/c++堆详解下篇（堆排序，TopK问题）

6.1.数据结构-c/c++堆详解下篇（堆排序，TopK问题）

上篇：6.1.数据结构-c/c++模拟实现堆上篇（向下，上调整算法，建堆，增删数据）-CSDN博客 本章重点 1.使用堆来完成堆排序 2.使用堆解决TopK问题 目录 一.堆排序 1.1 思路 1.2 代码 1.3 简单测试 二.TopK问题 2.1 思路(求最小)： 2.2 C语言代码（手写堆） 2.3 C++代码（使用优先级队列 priority_queue）
阅读更多...
《数据结构（C语言版）第二版》第八章-排序（8.3-交换排序、8.4-选择排序）

《数据结构（C语言版）第二版》第八章-排序（8.3-交换排序、8.4-选择排序）

8.3 交换排序 8.3.1 冒泡排序 【算法特点】 (1) 稳定排序。 (2) 可用于链式存储结构。 (3) 移动记录次数较多，算法平均时间性能比直接插入排序差。当初始记录无序，n较大时， 此算法不宜采用。 #include <stdio.h>#include <stdlib.h>#define MAXSIZE 26typedef int KeyType;typedef char In
阅读更多...
树（Tree）——《啊哈！算法》

树（Tree）——《啊哈！算法》

树 什么是树？树是一种特殊的图，不包含回路的连通无向树。 正因为树有着“不包含回路”这个特点，所以树就被赋予了很多特性。 一棵树中的任意两个结点有且仅有唯一的一条路径连通。一棵树如果有n个结点，那么它一定恰好有n-1条边。在一棵树中加一条边将会构成一个回路。 一棵树有且只有一个根结点。 没有父结点的结点称为根结点（祖先）。没有子结点的结点称为叶结点。如果一个结点既不是根结点也不是叶
阅读更多...
【408数据结构】散列 （哈希）知识点集合复习考点题目

【408数据结构】散列 （哈希）知识点集合复习考点题目

苏泽  “弃工从研”的路上很孤独，于是我记下了些许笔记相伴，希望能够帮助到大家    知识点 1. 散列查找 散列查找是一种高效的查找方法，它通过散列函数将关键字映射到数组的一个位置，从而实现快速查找。这种方法的时间复杂度平均为(
阅读更多...
浙大数据结构：树的定义与操作

浙大数据结构：树的定义与操作

四种遍历 #include<iostream>#include<queue>using namespace std;typedef struct treenode *BinTree;typedef BinTree position;typedef int ElementType;struct treenode{ElementType data;BinTree left;BinTre
阅读更多...
Python 内置的一些数据结构

Python 内置的一些数据结构

文章目录 1. 列表 (List)2. 元组 (Tuple)3. 字典 (Dictionary)4. 集合 (Set)5. 字符串 (String) Python 提供了几种内置的数据结构来存储和操作数据，每种都有其独特的特点和用途。下面是一些常用的数据结构及其简要说明： 1. 列表 (List) 列表是一种可变的有序集合，可以存放任意类型的数据。列表中的元素可以通过索
阅读更多...
浙大数据结构：04-树7 二叉搜索树的操作集

浙大数据结构：04-树7 二叉搜索树的操作集

这道题答案都在PPT上，所以先学会再写的话并不难。 1、BinTree Insert( BinTree BST, ElementType X ) 递归实现，小就进左子树，大就进右子树。 为空就新建结点插入。 BinTree Insert( BinTree BST, ElementType X ){if(!BST){BST=(BinTree)malloc(sizeof(struct TNo
阅读更多...
【数据结构入门】排序算法之交换排序与归并排序

【数据结构入门】排序算法之交换排序与归并排序

前言         在前一篇博客，我们学习了排序算法中的插入排序和选择排序，接下来我们将继续探索交换排序与归并排序，这两个排序都是重头戏，让我们接着往下看。  一、交换排序 1.1 冒泡排序 冒泡排序是一种简单的排序算法。 1.1.1 基本思想 它的基本思想是通过相邻元素的比较和交换，让较大的元素逐渐向右移动，从而将最大的元素移动到最右边。 动画演示： 1.1.2 具体步
阅读更多...
数据结构：线性表的顺序存储

数据结构：线性表的顺序存储

文章目录 🍊自我介绍🍊线性表的顺序存储介绍概述例子 🍊顺序表的存储类型设计设计思路类型设计 你的点赞评论就是对博主最大的鼓励 当然喜欢的小伙伴可以：点赞+关注+评论+收藏（一键四连）哦~ 🍊自我介绍   Hello,大家好，我是小珑也要变强（也是小珑），我是易编程·终身成长社群的一名“创始团队·嘉宾” 和“内容共创官” ,现在我来为大家介绍一下有关物联网-嵌入
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2