吴恩达机器学习-可选实验室：逻辑回归的成本函数（Cost Funtion for Logistic Regression）

本文主要是介绍吴恩达机器学习-可选实验室：逻辑回归的成本函数（Cost Funtion for Logistic Regression），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目标

在本实验中，你将:检查执行情况并利用成本函数进行逻辑回归。

import numpy as np
%matplotlib widget
import matplotlib.pyplot as plt
from lab_utils_common import  plot_data, sigmoid, dlc
plt.style.use('./deeplearning.mplstyle')

数据集

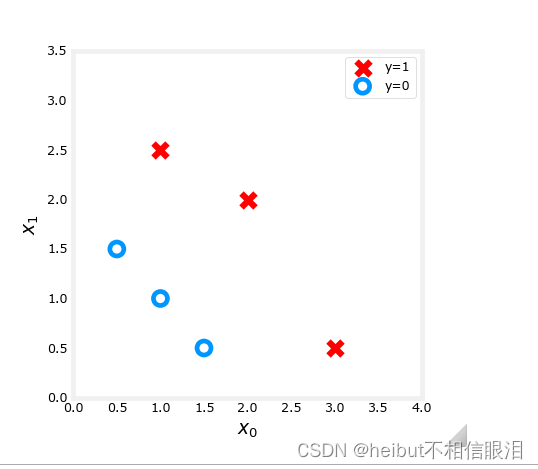
让我们从决策边界实验室中使用的相同数据集开始。

X_train = np.array([[0.5, 1.5], [1,1], [1.5, 0.5], [3, 0.5], [2, 2], [1, 2.5]])  #(m,n)
y_train = np.array([0, 0, 0, 1, 1, 1])                                           #(m,)

我们将使用一个辅助函数来绘制这些数据。标签y = 1的数据点显示为红色标记为y = 0的数据点用蓝色圆圈表示。

成本函数

在之前的实验中，你开发了逻辑损失函数。回想一下，loss被定义为应用于一个示例。在这里，您将损失组合起来形成成本，其中包括所有示例。
回想一下，对于逻辑回归，成本函数是这样的形式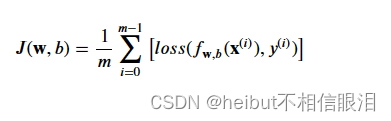

代码描述

compute_cost_logistic循环的算法遍历所有示例，计算每个示例求和的损失。注意变量X和y不是标量值，而是形状分别为(m, n)和(m，)的矩阵，其中n是特征的数量，m是训练样例的数量。

def compute_cost_logistic(X, y, w, b):"""Computes costArgs:X (ndarray (m,n)): Data, m examples with n featuresy (ndarray (m,)) : target valuesw (ndarray (n,)) : model parameters  b (scalar)       : model parameterReturns:cost (scalar): cost"""m = X.shape[0]cost = 0.0for i in range(m):z_i = np.dot(X[i],w) + bf_wb_i = sigmoid(z_i)cost +=  -y[i]*np.log(f_wb_i) - (1-y[i])*np.log(1-f_wb_i)cost = cost / mreturn cost

使用下面的单元格检查成本函数的实现。

w_tmp = np.array([1,1])
b_tmp = -3
print(compute_cost_logistic(X_train, y_train, w_tmp, b_tmp))

例子

现在，让我们看看对于不同的w值，代价函数的输出是什么。

• 在之前的实验中，您绘制了b = -3, w0 = 1, w1 = 1的决策边界。也就是说，w= np.array([- 3,1,1])。

• 假设你想知道b = -4, w0 = 1, w1 = 1，或者w = np.Array([- 4,1,1])提供了一个更好的模型。

让我们首先绘制这两个不同b值的决策边界，看看哪一个更适合数据。

• 对于b=-3, w0 =1, w1=1，我们画出-3+xo +x=0(用蓝色表示)
• 对于b=-4, w0=1,w1=1，我们画出-4+xo+x=0(用洋红色表示)

import matplotlib.pyplot as plt# Choose values between 0 and 6
x0 = np.arange(0,6)# Plot the two decision boundaries
x1 = 3 - x0
x1_other = 4 - x0fig,ax = plt.subplots(1, 1, figsize=(4,4))
# Plot the decision boundary
ax.plot(x0,x1, c=dlc["dlblue"], label="$b$=-3")
ax.plot(x0,x1_other, c=dlc["dlmagenta"], label="$b$=-4")
ax.axis([0, 4, 0, 4])# Plot the original data
plot_data(X_train,y_train,ax)
ax.axis([0, 4, 0, 4])
ax.set_ylabel('$x_1$', fontsize=12)
ax.set_xlabel('$x_0$', fontsize=12)
plt.legend(loc="upper right")
plt.title("Decision Boundary")
plt.show()

你可以从这张图中看到。对于训练数据，Array([- 4,1,1])是一个较差的模型。让我们看看成本函数的实现是否反映了这一点

w_array1 = np.array([1,1])
b_1 = -3
w_array2 = np.array([1,1])
b_2 = -4print("Cost for b = -3 : ", compute_cost_logistic(X_train, y_train, w_array1, b_1))
print("Cost for b = -4 : ", compute_cost_logistic(X_train, y_train, w_array2, b_2))

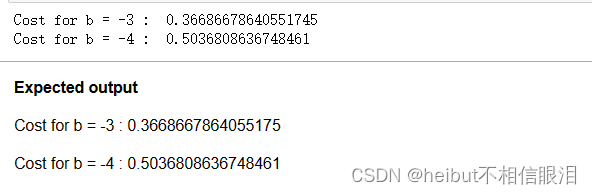
您可以看到成本函数的行为与预期一致，并且成本w = np.array([- 4,1,1])确实比w=np.array[-3,1,1]的代价高

恭喜

在本实验中，您检查并使用了逻辑回归的成本函数。

这篇关于吴恩达机器学习-可选实验室：逻辑回归的成本函数（Cost Funtion for Logistic Regression）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---