代码随想录算法训练营day53|第九章 动态规划part14

体会一下本题和 718. 最长重复子数组 的区别  

视频讲解：动态规划子序列问题经典题目 | LeetCode：1143.最长公共子序列_哔哩哔哩_bilibili

代码随想录

首先这道题肯定是要用二维数组来做的，一维数组倒不清楚从哪里来的结果。dp[i][j]表示长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]，道理同样是便于在text字符串下标为0的时候依然符合递推公式。

主要就是两大情况： text1[i - 1] 与 text2[j - 1]相同，text1[i - 1] 与 text2[j - 1]不相同。

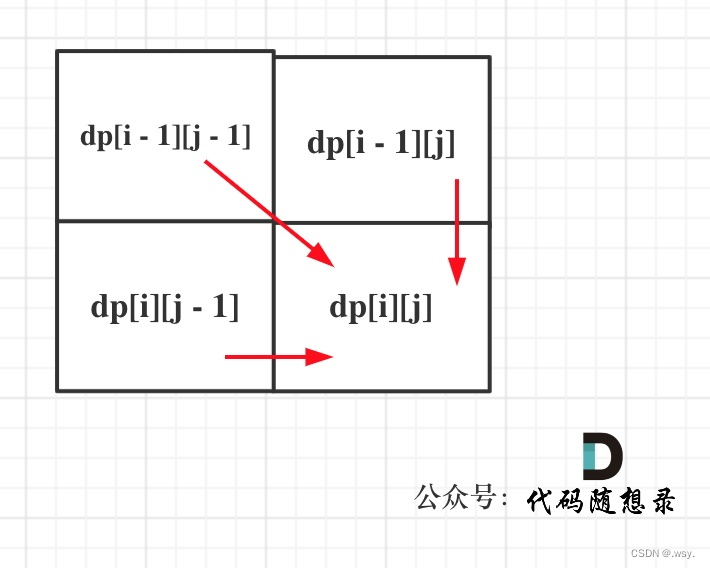
如果text1[i - 1] 与 text2[j - 1]相同，也就是找到了一个公共元素，故而也就要在原来的基础上加一，所谓原来的基础也就是左上角的dp[i-2][j-2]，为什么要让指向两个字符串的指针同时往回退一个就储存着原来的基础呢，这是因为既然text1的（i - 1）处和text2的（j - 1)处所对应的元素相等，那就要往前倒，看[0, i - 2]和[0, j - 2]范围内的情况是怎样的，所以dp[i][j] = dp[i - 1][j - 1] + 1;

如果text1[i - 1] 与 text2[j - 1]不相同，既然不能使得长度加一了，那为了之后的推导也要为这个位置赋一个值，这个值必须表示长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列，那就看看周围的text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，即取最大的：dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])。（e.g. ace 和 acbde 两个字符串在遍历到 i = 2,j = 2的时候遇到了不相等的情况，就考虑ac和acb的情况、ace和ac的情况）

至于初始化，第一行列是和空字符串进行比较的，所以自然为0，而别的值也会被覆盖掉，所以都赋值成0更加省事。

遍历顺序只要知道从哪里得到的dp[i][j]即可，先初始化先推导要用到的值。

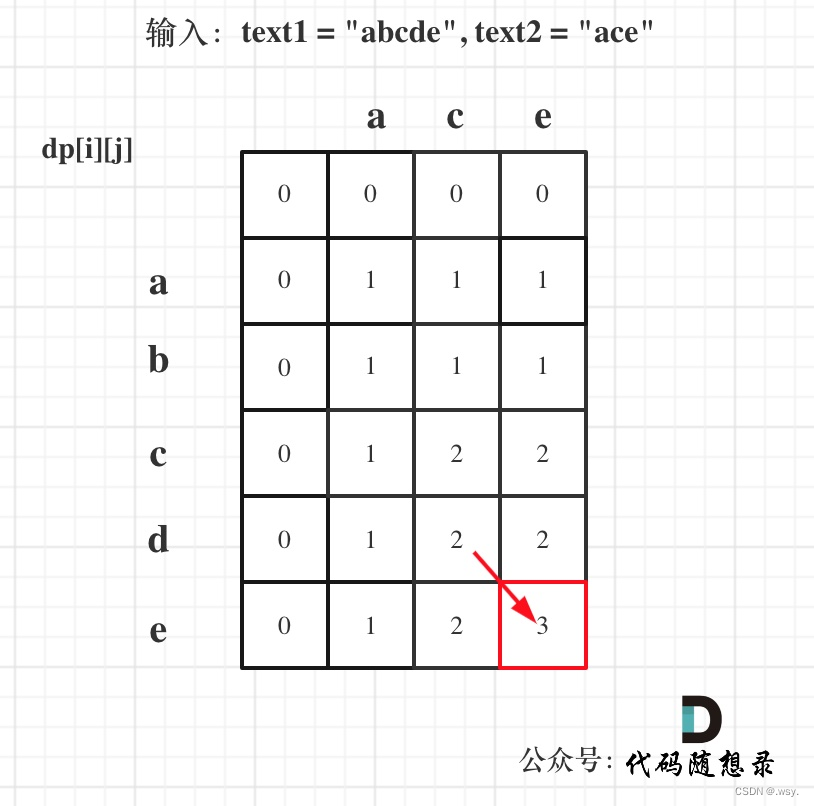
举例推导dp数组——

int longestCommonSubsequence(string text1, string text2) {vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));for (int i = 1; i <= text1.size(); i++) {for (int j = 1; j <= text2.size(); j++) {if (text1[i - 1] == text2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;} else {dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}}return dp[text1.size()][text2.size()];}

1035.不相交的线 

其实本题和 1143.最长公共子序列 是一模一样的，大家尝试自己做一做。

视频讲解：动态规划之子序列问题，换汤不换药 | LeetCode：1035.不相交的线_哔哩哔哩_bilibili

代码随想录

确实是和上面的题目是一毛一样的，稍微改改变量上面的代码就能AC。

53. 最大子序和 

这道题我们用贪心做过，这次 再用dp来做一遍 

视频讲解：看起来复杂，其实是简单动态规划 | LeetCode：53.最大子序和_哔哩哔哩_bilibili

代码随想录

感觉和上面的题真是没有一点关系。推导公式很容易懂：dp[i] = max(dp[i - 1] + nums[i], nums[i])，因为正向推导，所以必须初始化dp[0]，因为最少包含一个元素，所以可以初始化为nums[0]本身。然后注意因为dp数组是要考虑全部的数在内的所以不一定是最大值，虽然确实是包括下标i（以nums[i]为结尾）的最大连续子序列和为dp[i]，但真的最大和的子列不一定包含当前这个数，所以需要实时更新的，然后res也必须初始化为nums[0]，防止nums只有一个元素的情况出现。

int maxSubArray(vector<int>& nums) {if (nums.size() == 0) return 0;vector<int> dp(nums.size());dp[0] = nums[0];int result = dp[0];for (int i = 1; i < nums.size(); i++) {dp[i] = max(dp[i - 1] + nums[i], nums[i]); // 状态转移公式if (dp[i] > result) result = dp[i]; // result 保存dp[i]的最大值}return result;}