RLAIF（0）—— DPO（Direct Preference Optimization） 原理与代码解读

本文主要是介绍RLAIF（0）—— DPO（Direct Preference Optimization） 原理与代码解读，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

之前的系列文章：介绍了 RLHF 里用到 Reward Model、PPO 算法。
但是这种传统的 RLHF 算法存在以下问题：流程复杂，需要多个中间模型对超参数很敏感，导致模型训练的结果不稳定。
斯坦福大学提出了 DPO 算法，尝试解决上面的问题，DPO 算法的思想也被后面 RLAIF（AI反馈强化学习）的算法借鉴，这个系列会从 DPO 开始，介绍 SPIN、self-reward model 算法。
而 DPO 本身是一种不需要强化学习的算法，简化了整个 RLHF 流程，训练起来会更简单。

原理

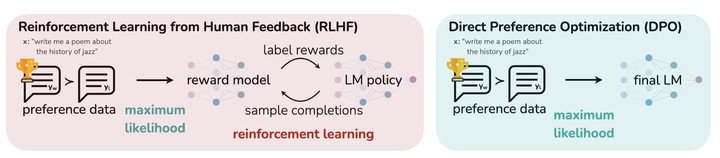
传统的 RLHF 步骤一般是：训练一个 reward model 对 prompt 的 response 进行打分，训练完之后借助 PPO 算法，使得 SFT 的模型和人类偏好对齐，这个过程我们需要初始化四个基本结构一致的 transformer 模型。DPO 算法，提供了一种更为简单的 loss function，而这个就是 DPO 的核心思想：针对奖励函数的 loss 函数被转换成针对策略的 loss 函数，而针对策略的 loss 函数又暗含对奖励的表示，即人类偏好的回答会暗含一个更高的奖励。

$${\mathcal{L}}_{\mathrm{DPO}}\left({\pi }_{\theta };{\pi }_{\mathrm{ref}}\right)=-{\mathbb{E}}_{\left(x,y_w,y_l\right)\sim \mathcal{D}}\left[\log \sigma \left(\beta \log \frac{{\pi }_{\theta }\left(y_w\mid x\right)}{{\pi }_{\mathrm{ref}}\left(y_w\mid x\right)}-\beta \log \frac{{\pi }_{\theta }\left(y_l\mid x\right)}{{\pi }_{\mathrm{ref}}\left(y_l\mid x\right)}\right)\right]$$

这个函数唯一的超参数是 $\beta$，决定了不同策略获得的奖励之间的 margin。
可以看出 DPO 虽然说是没有用强化学习，但是还是有强化学习的影子，相当于 beta 是一个固定的 reward，通过人类偏好数据，可以让这个奖励的期望最大化，本至上来说 dpo 算法也算是一种策略迭代。
对 loss function 求导，可得如下表达式：

$$\begin{array}{rl}& {\nabla }_{\theta }{\mathcal{L}}_{\mathrm{DPO}}\left({\pi }_{\theta };{\pi }_{\mathrm{ref}}\right)=\\ & -\beta {\mathbb{E}}_{\left(x,y_w,y_l\right)\sim \mathcal{D}}[\underset{\text{higher weight when reward estimate is wrong }}{\underbrace{\sigma \left({\hat{r}}_{\theta }\left(x,y_l\right)-{\hat{r}}_{\theta }\left(x,y_w\right)\right)}}[\underset{\text{increase likelihood of }{y}_w}{\underbrace{{\nabla }_{\theta }\log \pi \left(y_w\mid x\right)}}-\underset{\text{decrease likelihood of }{y}_l}{\underbrace{{\nabla }_{\theta }\log \pi \left(y_l\mid x\right)}}]]\end{array}$$

其中 ${\hat{r}}_{\theta }(x,y)=\beta \log \frac{{\pi }_{\theta }(y\mid x)}{{\pi }_{\text{ref }}(y\mid x)}$ 。
不得不佩服作者构思的巧妙，通过求导，作者捕捉到了”暗含“的 reward —— $\sigma \left({\hat{r}}_{\theta }\left(x,y_l\right)-{\hat{r}}_{\theta }\left(x,y_w\right)\right)$，作者在论文里说到，当我们在让 loss 降低的过程中，这个 reward 也会变小（可以用来做 rejected_rewards）。因而在下面的代码实现里，chosen_rewards 和 rejected_rewards 就来自这个想法。

代码实现

我们来看下 trl 是如何实现 dpo loss 的，可以看到 dpo 和 ppo 相比，实现确实更为简单，而且从开源社区的反应来看，dpo 的效果也很不错，现在 dpo 已经成为偏好对齐最主流的算法之一。

def dpo_loss(self,policy_chosen_logps: torch.FloatTensor,policy_rejected_logps: torch.FloatTensor,reference_chosen_logps: torch.FloatTensor,reference_rejected_logps: torch.FloatTensor,
) -> Tuple[torch.FloatTensor, torch.FloatTensor, torch.FloatTensor]:"""Compute the DPO loss for a batch of policy and reference model log probabilities.Args:policy_chosen_logps: Log probabilities of the policy model for the chosen responses. Shape: (batch_size,)policy_rejected_logps: Log probabilities of the policy model for the rejected responses. Shape: (batch_size,)reference_chosen_logps: Log probabilities of the reference model for the chosen responses. Shape: (batch_size,)reference_rejected_logps: Log probabilities of the reference model for the rejected responses. Shape: (batch_size,)Returns:A tuple of three tensors: (losses, chosen_rewards, rejected_rewards).The losses tensor contains the DPO loss for each example in the batch.The chosen_rewards and rejected_rewards tensors contain the rewards for the chosen and rejected responses, respectively."""pi_logratios = policy_chosen_logps - policy_rejected_logpsif self.reference_free:ref_logratios = torch.tensor([0], dtype=pi_logratios.dtype, device=pi_logratios.device)else:ref_logratios = reference_chosen_logps - reference_rejected_logpspi_logratios = pi_logratios.to(self.accelerator.device)ref_logratios = ref_logratios.to(self.accelerator.device)logits = pi_logratios - ref_logratios# The beta is a temperature parameter for the DPO loss, typically something in the range of 0.1 to 0.5.# We ignore the reference model as beta -> 0. The label_smoothing parameter encodes our uncertainty about the labels and# calculates a conservative DPO loss.losses = (-F.logsigmoid(self.beta * logits) * (1 - self.label_smoothing)- F.logsigmoid(-self.beta * logits) * self.label_smoothing)chosen_rewards = (self.beta* (policy_chosen_logps.to(self.accelerator.device) - reference_chosen_logps.to(self.accelerator.device)).detach())rejected_rewards = (self.beta* (policy_rejected_logps.to(self.accelerator.device)- reference_rejected_logps.to(self.accelerator.device)).detach())return losses, chosen_rewards, rejected_rewards

改进

在 Preference Tuning LLMs with Direct Preference Optimization Methods (huggingface.co) 一文中提到，dpo 也存在一些不足：
dpo 算法很容易在数据集上过拟合dpo 训练依赖成对的偏好数据集，这种数据集的构造和标注都很耗费时间。
一些研究者也根据这些问题提出了新的算法：
针对 1，deepmind 提出了 Identity Preference Optimisation (IPO)，给 DPO 的 loss 加了一个正则项，避免训练快速过拟合
针对 2，ContextualAI 提出了 Kahneman-Tversky Optimisation (KTO)，KTO 算法的数据集，不再是成对的偏好数据集，而是给每条数据集 “good” 或者 “bad” 的标签进行偏好对齐。
这些算法的相关内容会在介绍完 SPIN 和 self-reward model 之后进行补充，欢迎关注，感谢阅读。
最后说点题外话，通过 DPO，我们可以看出深度学习还是一门实验的学科，如果光看 DPO 算法本身，很难相信这样一个简单的算法，会这么有效。所以多动手写代码，多实验，也许有一天我们也可以发现很 work 的算法，共勉。

参考

1. Direct Preference Optimization: Your Language Model is Secretly a Reward Model
2. Aligning LLMs with Direct Preference Optimization (youtube.com)
3. huggingface/trl: Train transformer language models with reinforcement learning. (github.com)
4. Preference Tuning LLMs with Direct Preference Optimization Methods (huggingface.co)

这篇关于RLAIF（0）—— DPO（Direct Preference Optimization） 原理与代码解读的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---