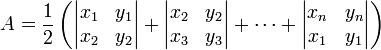多边形质心（centroid）的计算方法

本文主要是介绍多边形质心（centroid）的计算方法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

原文代码

// polygon按顺时针排列顶点
function getCentroid(polygon) {var totalArea = 0var totalX = 0var totalY = 0var points = polygon[0]for (var i = 0; i < points.length; ++i) {// a、b以及原点构成一个三角形var a = points[i + 1]var b = points[i]var area = 0.5 * (a[0] * b[1] - b[0] * a[1])  // 计算面积var x = (a[0] + b[0]) / 3  // 计算x方向质心var y = (a[1] + b[1]) / 3  // 计算y方向质心totalArea += areatotalX += area * xtotalY += area * y}return [totalX / totalArea, totalY/ totalArea]
}

See https://jingsam.github.io/2016/10/05/centroid.html

这篇关于多边形质心（centroid）的计算方法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---