Photometric Stereo 光度立体三维重建（四）—

本文主要是介绍Photometric Stereo 光度立体三维重建（四）——光源标定，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

光源标定是进行光度立体三维重建的第一步，本文将介绍两种光源标定方法——基于金属球反射的标定以及基于“SFM”思想的标定

1.基于金属球反射的标定

标定光源的一种方法是使用金属球，在排到的金属球的照片上面的最亮的点指明了光源的方向

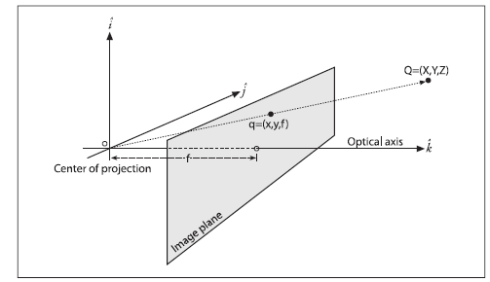
来源于http://pages.cs.wisc.edu/~csverma/CS766_09/Stereo/stereo.html的示意图：
在这里插入图片描述
然而，这幅示意图的几何向量标注具有一定的误导性，我将其换个角度表示以便展开光源方向的推导：

其中，反射方向R是固定的（因为它一直正对着观察者）:
$\ \mathbf{R}=[0,0,1]^T$
我们取 $P_x,P_y$ 为最亮点在图像中的像素坐标位置， $C_x, C_y$ 为金属球在图像中的中心点（可以由mask图像确定）,由此我们可以求出法线向量 $\ \mathbf{N}=[N_x,N_y.N_z]^T$ :
$N_x=P_x-C_x$ $N_y=P_y-C_y$ $\ N_z = \sqrt{(R^2-N_x^2-N_y^2)}$
N_z中的R是球的半径

求得法线向量后，我们可以知道：
$\ \mathbf{R}+\mathbf{L}=\mathbf{N}=2\mathbf{S}$ $\ \mathbf{L}=2\mathbf{S}-\mathbf{R}$
我们现在转移到求S，因为S是R在N上的投影（向量投影计算可参考这里），因此可以得到：
$\ \mathbf{S}=\frac{(\mathbf{R}·\mathbf{N})}{|\mathbf{N}|^2}\mathbf{N}=(\mathbf{R}·\mathbf{N})\mathbf{N}$
带入L的表达式，可得：
$\ \mathbf{L}=2(\mathbf{N·\mathbf{R}})\mathbf{R}-\mathbf{R}$
我们便可以利用上式求解光源方向

2.基于“SFM”的光源标定

论文标题：Light Structure from Pin Motion: Geometric Point Light Source Calibration（ECCV2018 / IJCV2020）

2.0 SFM简单回顾

SFM(structure from motion)目的是从图像特征点的对应同时恢复3D结构（3D点的位置）和姿态（相机的外参数）
设 $P_w$ 是世界坐标系的一个点， $P_c$ 是 $P_w$ 在相机坐标系中的位置，则有 $\ P_c=[R \quad t]P_w$ ，该点在成像平面的齐次坐标为 $\ p=[\mu,v,1]^T$ ，其在归一化平面的坐标为 $x=[X_c/Z_c,Y_c/Z_c,1]$ ，有 $p=Kx，x=K^{-1}p$ ，则通过对极几何约束，我们可以获得同一个特征点在两幅图像（相机在两个姿态）下坐标的对应关系：
对于本质矩阵
$\ E=[t]_\times R$
和基础矩阵
$F=K^{-T}EK^{-1}$
本质矩阵表征了点在两个姿态下归一化平面坐标的对应关系：
$x_2^TEx_1=0$
基础矩阵表征了点在两个姿态下齐次像素坐标的对应关系：
$p_2^TFp_1=0$
考虑 $\ E$ 的尺度等价性，我们可以使用八点法来求解基础矩阵 $\ E$

在求出 $\ E$ 后，可以通过SVD分解求出 $\ R和t$

如果场景中的特征点都落在同一平面上，则可以通过单应矩阵 $\ H$ 来进行运动估计，单应矩阵描述了两个平面间的映射关系，对于图像 $I_1,I_2$ 中匹配好的落在同一个平面上的特征点 $p_1,p_2$ ，其对应关系为：
$\ p_2=K(R-\frac{tn^T}{d})K^{-1}p_1=Hp_1$

单应矩阵可以通过4对匹配特征点算出（特征点不能三点共线）

在估计出相机运动后，可以通过三角测量估计出地图点的深度。

2.1 方法介绍

在第一节所介绍的用金属球进行标定的方法中，存在以下的弊端：
1.需要拥有相对精确的球体
2.需要注释出每个图像的高亮中心
3.需要标出图像中球的轮廓（mask）
4.小的标注误差会导致光源位置大的偏差

因此作者提出一种新的方法来进行光源的标定：作者通过在标定板上插上带有一定大小头部的针，通过在固定相机下改变标定板的姿态，从而获得当前光源的位置信息：

在这里插入图片描述
论文提出方法的流程图：

2.1.1阴影的形成模型

假设阴影接收平面π固定于世界坐标系的x-y平面

一个近点光源在世界坐标系的位置为：
$\ \mathbf{l}=[l_x,l_y,l_z]^T \in \mathbb{R}^3$
假设阴影制造物(caster)，即针头的位置为 $\ \mathbf{c} \in \mathbb{R}^3$ ，它产生的阴影在π平面上位置为 $\ \mathbf{s} \in \mathbb{R}^2$ ，在世界坐标系中位置是 $\ \overline{\mathbf{s}}=[\mathbf{s}^T,0]^T$ ，因为 $\ \mathbf{l},\mathbf{c},\overline{\mathbf{s}}$ 在同一直线上，因此由其中两个点组成的任意两直线是平行的，因此可以得出：
在这里插入图片描述
将

代入（1）式得：

将叉积展开得到：

从中可以求出sx和sy：

我们将s写为齐次坐标，并使用缩放因子 $\ \gamma$ ，得到：

继续整理得：

将等号右边改写为矩阵相乘的形式得：

我们称 $\ \mathbf{L}$ 为光矩阵，我们将其分解可以得到其内参和外参：
在这里插入图片描述
以上是关于近点光源的，对于远点光源，光线是平行的，因此光向量应该指光源的方向，而不是光源点的位置，因此(1)变为：

同理我们可以整理为：

我们发现对于远点光源，光矩阵(3,3)的位置是0，这个光矩阵类似于在相机矩阵中的正交投影

我们希望将近点光源和远点光源的光矩阵统一起来，在齐次坐标中，相差一个常数的缩放是等价的，因此我们把两个光矩阵都除以 $l_z$ ，得到：
在这里插入图片描述
可以发现，当光源无限远时，近点光源光矩阵变为远点光源光矩阵，因此我们使用下式作为统一的阴影投影等式：

这也是为什么论文名为Light Structure from Pin Motion的原因，论文中恢复光源方向的思想是跟SFM类似的，点光源和针孔相机可以被相似的数学模型所描述，其相似的对应关系为：
1.点光源=针孔相机
2.阴影接收面=图像平面（成像面）
3.阴影caster=场景点
4.光矩阵L=相机投影矩阵 $\ P=KT=K[R|t]$

Light Structure from Pin Motion与SFM的对比：
在这里插入图片描述

2.1.2 阴影对应中的对极几何

回顾SFM，相机运动的求解是基于对极几何约束的，那么，在Light Structure from Pin Motion中，也应该找出阴影对应的对极几何约束。

作者移动光源，同时casters和阴影接收面是静止的，在其中分析阴影的对应关系，这类似于SFM中移动的相机与静置的场景点。

阴影的对极几何关系图：
在这里插入图片描述
caster是静置且位置未知的，对于由光源 $l_1$ 投影得到的阴影 $\ s$ ，caster可以在线段 $l_1s$ 上的任意位置，当光源位置移动到 $l_2$ 时，一系列阴影的可能位置形成一条线，这相当于相机对极几何中的极线。

我们现在希望构造出阴影对极几何中的基础矩阵 $\ F$

记 $\ c$ 是caster的位置， $\ l_1 \neq l_2$ 是在标定目标坐标系下的光的位置， $L_i是l_i$ 的光矩阵， $L_1^+=(L_1^TL_1)^{-1}L_1^T是L_1$ 的伪逆， $\ \empty_{L_1} \in null(L_1)$ 是 $L_1$ 一维零空间下的非零向量， $\ \eta$ 是一个缩放常量，我们可以得到：

在这里插入图片描述
对上式左乘 $\ \tilde{s}_2^T[L_2 \empty_{L_1}]_\times$ ，得到：

由此我们得到了表征阴影对应的基础矩阵，对于 $L_i$
我们得到零空间向量 $\ \empty_{L_1}$

将其代入(5)式得到基础矩阵：

这个矩阵是反对称的，对于阴影 $\ \tilde{s_1}=[u,v,1]^T, \tilde{{s_2}=[u',v',1]}$ ，阴影的对极约束为：
在这里插入图片描述
因此我们可以解齐次线性方程组来求解在一个缩放因子下成立的系数f：

这实际上相当于估计只进行纯平移而不进行相对旋转的相机的常规的本质矩阵，由式(2)可以看出，旋转矩阵为单位阵

2.2 模型求解

论文提出的方法中，通过在固定点光源下从固定视点（相机位置固定）对标定目标进行多次观察，同时改变标定目标的姿态，自动实现点光源标定。阴影caster相对于校准目标的3D位置是未知的，这使得它特别容易建立目标，而问题仍然是易于处理的。

2.2.1 通过光束平差法标定光源方向

目标：通过观察投影自未知caster的阴影求出(4)中的 $\ l$ 。一次观察不足以提供充分的信息，因为我们让阴影接收面经历多个姿态 ${[R_i|t_i]\}$

在第i个姿态中，光源在接收面坐标系中的位置 $l_i$ 与在世界坐标系中的位置 $\ l$ 的关系为：
在这里插入图片描述
光矩阵 $L_i$ 为：

作者不仅使用多个姿态，更使用多个casters ${c_j\}$ 来提高校准精度，因此对于姿态i和caster j，我们得到阴影 $s_{ij}$ ，此时(4)变为：

假设目标姿态 ${[R_i|t_i]\}$ 已知，我们目标是估计光源在世界坐标系中的位置 $\ l$ 以及caster在标定目标坐标系中的位置 $c_j$ ，我们通过最小化重投影误差构建一个最小二乘问题：
在这里插入图片描述
可以使用LM算法来求解这个非线性最小二乘问题，为了鲁棒的估计使用随机抽样一致性(RANSAC)算法：我们不断选取一个随机的观测集，估计 $\ (l,c_j,\lambda_{ij})$ ，选择有最小残差的一个

2.2.2 Bundle Adjustment的初始化

（1）近点光源
类似于式(1)，我们可以写出：
在这里插入图片描述
将

代入得到：

其中，

我们可以重写上式为：

扩展叉积得到：

我们将它整理一下，得到：

其矩阵形式为：

这个方程包含一个观测结果，即姿态i和caster j的结合，但是我们需要堆砌多个观测下的方程。为了简化步骤，我们先将(18)分为几个子矩阵:
在这里插入图片描述
让 $N_p,N_c$ 为目标姿态和casters的数量，可以得到整个系统的方程为：

因为所有的观测共享 $l=[l_x,l_y,l_z]^T$ ，每个 $\ \theta_j$ 有12个未知数，因此我们有 $3+12N_c$ 个未知数

为了防止外点的影响，我们通过L1最小化来鲁棒求解:
在这里插入图片描述
为了求解此式，我们要满足:

因此，不管casters有多少，5个姿态下的观测足以求解方程

解出 $\ \theta^*$ 后，我们忽视二阶变量如 $l_xc_{j,x}$ ，使用 $c_j^*,l^*$ 来初始化(17)

（2）远点光源
对于远点光源，矩阵A的秩为 $3+12N_c-1$ ，因此，不幸的是，我们不能使用(18)来处理远光，但我们可以自动检测这种情况，切换到对远光的方程，求解，并切换回(17)的BA。因此，用户不必为他们的场景选择一个光照模型。

我们通过构造近点光源的矩阵A，然后检测A的奇异值，如果最大和最小的奇异值之比大于4e+4，我们转换到远光求解

对于远光，类似于(3)，我们使用 $l_i=R_i^Tl$ 重写为：
在这里插入图片描述
类似得，我们将其整理得：

设置 $l=[l_x,l_y,1]^T$ (2自由度)得到：

整理得：

将其改写为矩阵形式，得：

其子矩阵的形式为：

多次观测的方程堆叠和求解类似于(19)(20)，为了求解这个线性方程组，我们要满足：
在这里插入图片描述
因此只需要4个姿态下的观测，因为对于远光的方程组求解得到的是光的方向(direction)，但光束平差法需要光的位置(position)，因此我们需要它们的一个转换。我们从其中一个casters开始，将光源不断移动到很远的地方：
在这里插入图片描述
c是世界坐标系下任意的caster的位置，k是大常数(10e+10)，hc是caster的高度

2.2.3 阴影对应

在(17)(18)(21)中，我们需要得到在不同图像 $\ \mathbf{I}_i$ 中同一个caster j产生阴影 $s_{ij}$ 的对应。形式上，阴影对应搜索意味着我们需要找到与图像之间对应阴影匹配的置换

设 $\ S$ 为阴影 $\ \{\tilde{s_i}\}$ , $\ S'$ 为阴影 $\ \{\tilde{s'_i}\}$ ，将其水平叠加成矩阵，对于基础矩阵，我们寻找：
在这里插入图片描述
也就是说， $\ S'$ 的每一列都是一个阴影向量，我们将置换矩阵 $\ P'$ 右乘，以对各个阴影向量进行排列，只有 $\ S'和S$ 的每一列对应的阴影向量是在两幅图像中一一对应时，基础矩阵的对极约束等式才为0

不同于传统的图像特征匹配，我们不能使用特征描述符来缩小搜索范围，因为我们希望阴影非常小（为了让阴影的中心可以精确定位），所以不能改变caster的形状以使其阴影与其他caster的阴影有明显区别

作者通过检测多幅图像对应的一致性以获得阴影对应

对应一致性检验
作者建立了两个图像池：已经建立了阴影对应的图像——确定池(established pool) 以及对应未知的图像——未知池(unknown pool)

确定池用一张随机的，未知的图像进行初始化，目的是将尽可能多的图像从未知池移动到确定池中

工作分为两个阶段，在第一个阶段中，在确定池随机选取图像 $I_e$ ，在未知池选取k张图像 $I_{i_1},...I_{i_k}$

假设
在这里插入图片描述
是一个二值函数，其为真的条件是：当且仅当对于图像 $I_a,I_b$ ， $I_a$ 中的阴影 $s_i$ 和 $I_b$ 中的阴影 $s_j$ 获得匹配，使得式（22）最小化

然后，如果：
在这里插入图片描述
成立（即，从确定池抽取的图像开始，与未知池的第一张图像匹配，然后未知池的第一张与第二张图像进行匹配，以此类推，通过第一张（确定池图像）到最后一张（未知池的最后一张图像）能沿着图像链一直对应下去），我们就将未知池的图像 $I_{i_1},...I_{i_k}$ 移动到确定池，为了使约束严格，作者在文章中选择k=3，一旦有一半的图像转移到了确定池，我们就转到第二个阶段

在第二个阶段中，假设确定池中所有的图像都是一致对应的。因此，如果我们考虑一个未知图像和一个caster，那么所有已确定的图像中对应于那个特定caster的所有阴影都应该匹配未知图像中的相同阴影，这适用于所有的阴影caster。我们随机选取一幅未知图像，验证这一准则，如果超过一半的已确定图像与未知图像的对应关系一致，将其移动到确定池，否则将其丢弃，当未知池为空时，第二阶段结束

阴影检测
作者使用模板匹配方法进行阴影检测

作者生成了由一条线和一个圆组成的阴影合成图像作为模板。为了处理变化的射影变换，生成的模板具有12个旋转角度，每个角度都有3个大小的模板（也就是有36个模板）。作者将输入图像二值化后再进行模板匹配。进一步，作者使用针头头部的颜色（红色）来区分头部和头部阴影

2.3 实际操作（代码）

论文的github仓库：https://github.com/hiroaki-santo/light-structure-from-pin-motion

（1）相机标定
论文的代码中是使用Arcuo码进行标记的，因此我们首先要制作Arcuo标定板：

import cv2
from cv2 import aruco
import numpy as npdic = aruco.getPredefinedDictionary(aruco.DICT_6X6_1000)
board = aruco.GridBoard_create(5, 7, 100, 10, dic)
img = np.zeros((600, 800))
img = aruco.drawPlanarBoard(board, (600, 800), img, 10, 1)
cv2.imshow("board", img)
cv2.waitKey(0)