Photometric Stereo 光度立体三维重建（三）——由法向量恢复深度

本文主要是介绍Photometric Stereo 光度立体三维重建（三）——由法向量恢复深度，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

本文分为三部分，第一部分是使用最小二乘法求解物体表面法向量，第二部分是利用求解得到的法向量求出物体表面的深度（物体表面的高度场），第三部分是将求出的高度场写成obj文件后使用MeshLab显示

1. 最小二乘求解物体表面法向量

Python代码
代码所使用的数据来自https://github.com/yasumat/RobustPhotometricStereo

import numpy as np
import cv2
import glob
from sklearn.preprocessing import normalize# 光源位置数据路径以及物体各帧图像的路径
lights_path = r'.\RobustPhotometricStereo\data\bunny\lights.npy'
bunny_path = r'.\RobustPhotometricStereo\data\bunny\bunny_lambert\*.npy'# 读取光源方向
# 读取到的是 L.T
Lt = np.load(lights_path) # 读取图像
M = []
for fname in sorted(glob.glob(bunny_path)):im = np.load(fname).astype(np.float32)im = cv2.cvtColor(im, cv2.COLOR_RGB2GRAY)if M == []:height, width = im.shapeM = im.reshape((-1, 1))else:M = np.append(M, im.reshape((-1, 1)), axis=1)
M = np.asarray(M)# 光度立体计算 使用最小二乘法
# M = NL <-> M.T = L.T N.T
N = np.linalg.lstsq(Lt, M.T)[0].T
N = normalize(N, axis=1)# 可视化
N = np.reshape(N, (height, width, 3))
N[:,:,0], N[:,:,2] = N[:,:,2], N[:,:,0].copy()
N = (N + 1.0) / 2.0
cv2.imshow('normal map', N)
cv2.waitKey()
cv2.destroyAllWindows()

生成的法向量图：

在以上提到的github项目里，有更多求解法向量的方法

2. 恢复物体表面深度（恢复高度场）

2.1 基本原理

参考：1.http://pages.cs.wisc.edu/~csverma/CS766_09/Stereo/stereo.html
2.https://www.zhihu.com/question/388447602/answer/1200616778

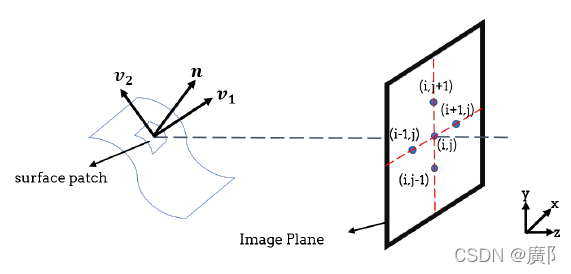
由图可知，物体surface patch的法向量n一定与v1和v2正交，该patch与图像平面(i,j)处的像素相对应，可以获得以下关系：

整理可得：

我们将物体区域内所有像素对应的深度排列成k维列向量z，k是物体区域像素总数，可以得到：

其中A的每一行只有两个非零元素1和-1，以其中一组方程组为例，上式的构造为：

求解这个稀疏线性方程组，便可以得到物体的深度，稀疏方程组的求解可以使用共轭梯度下降，Cholesky分解，LU分解等方法。

2.2 代码实现

这一节是基于上面所提到的github项目的，代码也是添加在其中

要在这个项目上基础上实现该功能，首先要对项目里demo.py中一段代码进行修改：

# Evaluate the estimate
N_gt = psutil.load_normalmap_from_npy(filename=GT_NORMAL_FILENAME)    # read out the ground truth surface normal
N_gt = np.reshape(N_gt, (rps.height*rps.width, 3))    # reshape as a normal array (p \times 3)
angular_err = psutil.evaluate_angular_error(N_gt, rps.N, rps.background_ind)    # compute angular error
print("Mean angular error [deg]: ", np.mean(angular_err[:]))
# 这里原代码有坑，他传入rps.N时，在函数里面转换了通道，因此如果用rps.N来恢复深度图，会出现错误，现在改为copy，就没问题了
psutil.disp_normalmap(normal=rps.N.copy(), height=rps.height, width=rps.width)
print("done.")

然后在demo.py的后面添加：

# 计算出深度图
rps.compute_depth()
rps.save_depthmap(filename="./est_depth")
psutil.disp_depthmap(depth=rps.depth, mask=rps.mask)

其中计算深度图的函数为

2.2.1 compute_depth()

我们前面提到过，numpixels的数量是mask里面非0像素数量，即物体的掩膜像素。

def compute_depth(self):"""计算出深度图原理参考: Mz = vM shape(2*numpixel, numpixel)z shape(numpixel, 1)v shape(2*numpixel, 1)1.http://pages.cs.wisc.edu/~csverma/CS766_09/Stereo/stereo.html2.https://www.zhihu.com/question/388447602/answer/1200616778"""im_h, im_w = self.mask.shapeN = np.reshape(self.N, (self.height, self.width, 3))# 得到掩膜图像非零值索引（即物体区域的索引）obj_h, obj_w = np.where(self.mask != 0)# 得到非零元素的数量no_pix = np.size(obj_h)# 构建一个矩阵 里面的元素值是掩膜图像索引的值full2obj = np.zeros((im_h, im_w))for idx in range(np.size(obj_h)):full2obj[obj_h[idx], obj_w[idx]] = idx# Mz = vM = scipy.sparse.lil_matrix((2*no_pix, no_pix))v = np.zeros((2*no_pix, 1))#--------- 填充M和v -----------## failed_rows = []for idx in range(no_pix):# 获取2D图像上的坐标h = obj_h[idx]w = obj_w[idx]# 获取表面法线n_x = N[h, w, 0]n_y = N[h, w, 1]n_z = N[h, w, 2]# z_(x+1, y) - z(x, y) = -nx / nzrow_idx = idx * 2if self.mask[h, w+1]:idx_horiz = full2obj[h, w+1]M[row_idx, idx] = -1M[row_idx, idx_horiz] = 1v[row_idx] = -n_x / n_zelif self.mask[h, w-1]:idx_horiz = full2obj[h, w-1]M[row_idx, idx_horiz] = -1M[row_idx, idx] = 1v[row_idx] = -n_x / n_z# else:#     failed_rows.append(row_idx)# z_(x, y+1) - z(x, y) = -ny / nzrow_idx = idx * 2 + 1if self.mask[h+1, w]:idx_vert = full2obj[h+1, w]M[row_idx, idx] = 1M[row_idx, idx_vert] = -1v[row_idx] = -n_y / n_zelif self.mask[h-1, w]:idx_vert = full2obj[h-1, w]M[row_idx, idx_vert] = 1M[row_idx, idx] = -1v[row_idx] = -n_y / n_z# else:#     failed_rows.append(row_idx)# # 将全零的行删除 对于稀疏矩阵M，要先将其恢复成稠密矩阵进行行删除再转为稀疏矩阵# M = M.todense()# M = np.delete(M, failed_rows, 0)# M = scipy.sparse.lil_matrix(M)# v = np.delete(v, failed_rows, 0)# 求解线性方程组 Mz = v  <<-->> M.T M z= M.T vMtM = M.T @ MMtv = M.T @ vz = scipy.sparse.linalg.spsolve(MtM, Mtv)std_z = np.std(z, ddof=1)mean_z = np.mean(z)z_zscore = (z - mean_z) / std_z# 因奇异值造成的异常outlier_ind = np.abs(z_zscore) > 10z_min = np.min(z[~outlier_ind])z_max = np.max(z[~outlier_ind])# 将z填充回正常的2D形状Z = self.mask.astype('float')for idx in range(no_pix):# 2D图像中的位置h = obj_h[idx]w = obj_w[idx]Z[h, w] = (z[idx] - z_min) / (z_max - z_min) * 255self.depth = Z

2.2.2 辅助函数

保存深度图：

def save_depthmap(self, filename=None):"""将深度图保存为npy格式:param filename: filename of a depth map:retur: None"""psutil.save_depthmap_as_npy(filename=filename, depth=self.depth)

def save_depthmap_as_npy(filename=None, depth=None):"""将深度图保存为npy:param filename: filename of the depth array:param normal: surface depth array:return: None"""if filename is None:raise ValueError("filename is None")np.save(filename, depth)

显示深度图

def disp_depthmap(depth=None, mask=None, delay=0, name=None):"""显示深度图:param depth: array of surface depth :param delay: duration (ms) for visualizing normal map. 0 for displaying infinitely until a key is pressed.:param name: display name:return: None"""if depth is None:raise ValueError("Surface depth `depth` is None")if mask is not None:depth = depth * maskdepth = np.uint8(depth)if name is None:name = 'depth map'cv2.imshow(name, depth)cv2.waitKey(delay)cv2.destroyAllWindows(name)cv2.waitKey(1)

生成的深度图：

3. 写入obj文件用MeshLab进行可视化

import scipy.io as sio
import cv2
import numpy as npdepth = np.load('est_depth.npy')
r, c = depth.shapef = open('bunny.obj', 'w')for i in range(r):for j in range(c):if depth[i, j] > 0:seq = 'v' + ' ' + str(float(i)) + ' ' + str(float(j)) + ' ' + str(depth[i, j]) + '\n'f.writelines(seq)f.close()

点云图：

我组建了一个光度立体技术的交流群，有兴趣的朋友可以一起来讨论一下！

这篇关于Photometric Stereo 光度立体三维重建（三）——由法向量恢复深度的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---