本文主要是介绍【计算机视觉】图像变换方法(边缘检测算子、霍夫变换、重映射、放射变换与直方图均衡化),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
来源:《OpenCV3编程入门》,怀念毛星云大佬🕯️
说明:本系列重点关注各种图像变换方法的原理、作用和对比
图像变换
图像变换(imagetransfrom),即将一幅图像转变成图像数据的另一种表现形式。变换最常见的例子就是傅里叶变换(Fouriertransform),即将图像转换成源图像数据的另一种表示形式。这类操作的结果仍然保存为OpenCV图像结构的形式,但是新图像的每个单独像素表示原始输出图像的频谱分量,而不是通常所考虑的空间分量。
基于OpenCV的边缘检测
边缘检测的一般步骤
- 【第一步】滤波
边缘检测的算法主要是基于图像强度的一阶和二阶异数,但导数通常对噪声很敏感,因此必须采用滤波器來改善与噪声有关的边缘检测器的性能。常见的滤波方法主要有高斯滤波,即采用离散化的高斯函数产生一组归一化的高斯核,然后基于高斯核函数对图像灰度矩阵的每一点进行加权求和。 - 【第二步】増强
增强边缘的基础是确定图像各点邻域强度的变化值。增强算法可以将图像灰度点邻域强度值有显著变化的点凸显出来。在具体编程实现时,可通过计算梯度幅值来确定。
-【第三步】检测
经过增强的图像,往往邻域中有很多点的梯度值比较大,而在特定的应用中,这些点并不是要找的边缘点,所以应该采用某种方法来对这些点进行取舍。实际工程中,常用的方法是通过阈值化方法来检测。
需要注意,算子都是带方向的,所以,示例中我们分别写了X方向、Y方向和最终合成的的效果图。
Canny算子
Canny边缘检测算法被很多人推崇为当今最优的边缘检测的算法。其中,Canny的目标是找到一个最优的边缘检测算法,让我们看一下最优边缘检测的三个主要评价标准。
- 低错误率:标识出尽可能多的实际边缘,同时尽可能地减少噪声产生的误报。
- 高定位性:标识出的边缘要与图像中的实际边缘尽可能接近。
- 最小响应:图像中的边缘只能标识一次,并且可能存在的图像噪声不应标识为边缘。
为了满足这些要求,Canny使用了变分法,这是一种寻找满足特定功能的函数的方法。最优检测用4个指数函数项的和表示.但是它非常近似于高斯函数的一阶导数。
Canny边缘检测的步骤:
- 【第一步】消除噪声
一般情况下, 使用高斯平滑滤波器卷积降噪。 以下显示了一个 size = 5 的高 斯内核示例:
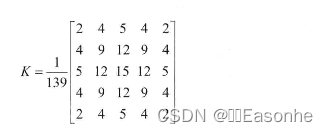
- 【第二步】计算梯度幅值和方向
此处,按照Sobel滤波器的步骤來操作。
①运用•对卷积阵列(分别作用于x和y方向)
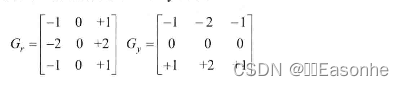
②使用下列公式计算梯度幅值和方向
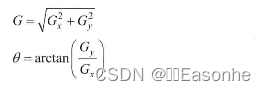
而梯度方向一般取这4个可能的角度之一——0度,45度,90度,135度。 - 【第三步】非极大值抑制
这一步排除非边缘像素,仅仅保留了一些细线条(候选边缘)。 - 【第四步】滞后阈值
这是最后一步,Canny使用了滞后阈值,滞后阈值需要两个阈值(高阈值和低阈值):
①若某一像素位置的幅值超过高阈值,该像素被保留为边缘像素。
②若某一像素位置的幅值小于低阈值,该像素被排除。
③若某…像素位置的幅值在两个阈值之间,该像紊仅仅在连接到一个高于高阈值的像素吋被保留。
sobel算子
Sobel算子是一个主要用于边缘检测的离散微分算子(discrete differentiation operator),它结合了高斯平滑和微分求导,用来计算图像灰度函数的近似梯度。在图像的任何一点使用此算子,都将会产生对应的梯度矢量或是其法矢量。
sobel算子的计算过程
我们假设被作用图像为I然后进行如下操作。
- 分别在X和y两个方向求导。
①水平变化:将丨与一个奇数大小的内核Gx进行卷积。比如,当内核大小为3时,Gx的计算结果为:
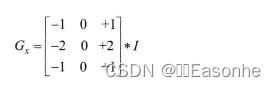
②垂直变化:将:丨与一个奇数大小的内核进行卷积。比如,当内核大小为3时,计算结果为:
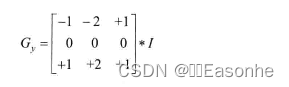
- 在图像的每一点,结合以上两个结果求出近似梯度:

另外有时,也可用下面更简单的公式代替:

Laplacian 算子
Laplacian 算子是n维欧几里德空叫中的-个二阶微分算子,定义为梯度grad的散度div。因此如果f是二阶可微的实函数,则f的拉普拉斯算子
定义如下。
(1) f的拉普拉斯算子也是笛卡儿平标系xi中的所有非混合二阶偏导数求和。
(2)作为一个二阶微分算子,拉普拉斯算子把C函数映射到C函数。对于k>=2,表达式(1)(或(2))定义了一个算子A:C®->C®;或更一般地,对于任何开集a,定义了一个算子△:C(Q)->C(Q)。
根据图像处理的原理可知,二阶导数可以用来进行检测边缘。因为图像是“二维”,需要在两个方向进行求导。使用Laplacian算子将会使求导过程变得简单。
Laplacian算子的定义:
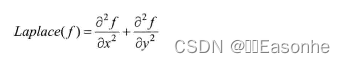
需要说明的是,由于Laplacian使用了图像梯度,它内部的代码其实是调用了Sobel算子的。让一幅图像减去它的Laplacian算子可以增强对比度。
scharr 滤波器
我们一般直接称scharr为滤波器,而不是算子。上文己经讲到,它在OpenCV 中主要是配合Sobel算子的运算而存在的。使用Scharr滤波器运算符计算x或y方向的图像差分
霍夫变换
在图像处理和计算机视觉领域中,如何从当前的图像中提取所需要的特征信息是图像识別的关键所在。在许多应用场景中需要快速准确地检测出直线或者圆。其中一种非常有效的解决问题的方法是霍夫(Hough)变换,其为图像处理中从图像中识别几何形状的基本方法之一,应用很广泛,也有很多改进算法。最基本的霍夫变换是从黑白图像中检测直线(线段)。
概述
霍夫变换(HoughTransform)是图像处理中的一种特征提取技术,该过程在一个参数空间中通过计算累计结果的局部最大值得到一个符合该特定形状的集合。作为霍夫变换结果。最初的Hough变换是设计用来检测直线和曲线的。起初的方法要求知道物体边界线的解析方程,
但不需要有关区域位置的先验知识。这种方法的一个突出优点是分割结果的Robustness,即对数据的不完全或噪声不是非常敏感。然而,要获得描述边界的解析表达常常是不可能的。经典霍夫变换用来检测图像中的直线,后来霍夫变换扩展到任意形状物体的识别,多为圆和椭圆。霍夫变换运用两个坐标空间之间的变换将在一个空间中具有相同形状的曲线或直线映射到另一个坐标空间的一个点上形成峰值,从而把检测任意形状的问题转化为统计峰值问题。翟夫变换在OpenCV中分为霍夫线变换和霍夫圆变换两种,下面将分别进行
介绍。
OpenCV中的霍夫线变换
我们知道,霍夫线变换是一种用来寻找直线的方法.在使用霍夫线变换之前,首先要对图像进行边缘检测的处理,即霍夫线变换的直接输入只能是边缘二值图像。OpenCV支持三种不同的霍夫线变换,它们分别是:标准霍夫变换(Standard Hough Transform.SHT),多尺度霍夫变换(Multi-Scale Hough Transform.MSHT)和累计概率霍夫变换(ProgressiveProbabilisticHoughTransform,PPHT)。其中,多尺度霍夫变换(MSHT)为经典霍夫变换(SHT)在多尺度下的一个变种。而累计概率霍夫变换(PPHT〉算法是标准霍夫变换(SHT)算法的一个改进,它在一定的范围内进行霍夫变换,计算单独线段的方向以及范围,从而减少计算量,缩短计算时间。之所以称PPHT为“概率”的,是因为并不将累加器平面内的所有可能的点累加,而只是累加其中的一部分,该想法是如果峰值如果足够髙,只用一小部分吋间去寻找它就够了。按照猜想,可以实质性地减少计算时间。而HoughLinesP函数用于调用累计概率霍夫变换PPHT。累计概率霍夫变换执行效率很高,所有相比于HoughLines函数,我们更倾向于使用HoughLinesP函数。
总结一下,OpenCV中的霍夫线变换有如下三种:
- 标准®夫变换(Standard Hough Transform,SHT),由HoughLines函数调用。
- 多尺度霍夫变换(Multi-Scale Hough Transform.MSHT),由HoughLines函数调用。
- 累计概率霍夫变换(Progressive Probabilistic Hough Transform,PPHT),由HoughLinesP函数调用。
原理
众所周知,一条直线在图像二维空间可由两个变量表示,有以下两种情况。如图所示。
① 在笛卡尔坐标系:可由参数斜率和截距(m,b)表示。
② 在极坐标系:可由参数极径和极角(r,表示。
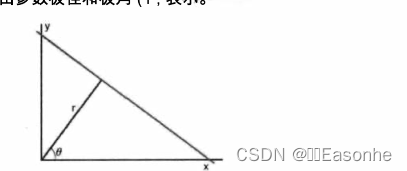
对于霍夫变换.我们将采用第二种方式极坐标系来表示直线.因此,直线的表达式可为:
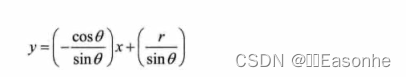
化简得
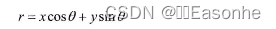
一般来说对于点(X0,Y0),可以将通过这个点的一族直线统一定义为:

这就意味着每一对(r„,0)代表一条通过点(x0,y0)的直线。
如果对于一个给定点我们在极坐标对极径极角平面绘出所有通过它的直线,将得到一条正弦曲线.例如,对于给定点x0=8和y0=6可以绘出所示平面图:
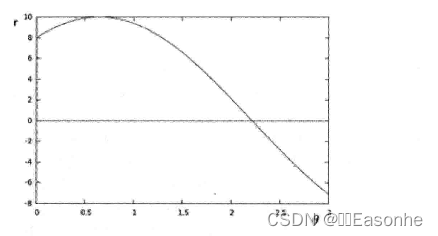
只绘出满足下列条件的点r>0和.0<0<2派
(4)我们可以对图像中所有的点进行上述操作.如果两个不同点进行上述操作后得到的曲线在平面0一r相交,这就意味着它们通过同一条直线。例如,接上面的例子继续对点x1=9,y1=4和点x2=12,y2=3绘图,得到图示:
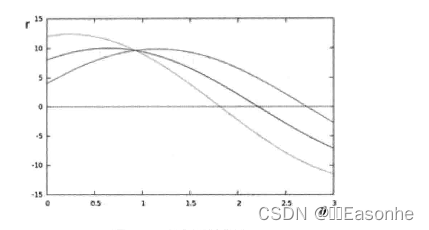
这三条曲线在平面相交于点(0.925,9.6),坐标表示的是参数对0_r或者是说点(x0,y0),点(x1,y1)和点(x2,y2)组成的平面内的的直线。
以上的说明表明,一般来说,一条直线能够通过在平面0一r寻找交于一点的曲线数量来检测。而越多曲线交于一点也就意味着这个交点表示的直线由更多的点组成。一般來说我们可以通过设置直线上点的阈值来定义多少条曲线交于一点,这样才认为检测到了一条直线。
这就是霍夫线变换要做的。它追踪图像中每个点对应曲线间的交点.如果交于一点的曲线的数量超过了阈值,那么可以认为这个交点所代表的参数对(0,r)在原图像中为一条直线。
霍夫圆变换
霍夫圆变换的基本原理和上曲讲的霍夫线变化大体上是很类似的,只是点对应的二维极径极角空间被三维的圆心点x、y和半径r空问取代。说“大体上类似”的原因是,如果完全用相同的方法的话,累加平面会被三维的累加容器所代替一在这三维中,一维是x,一维是y,另外一维是圆的半径r。这就意味着需要大量的内存而且执行效率会很低,速度会很慢。对直线來说,一条直线能由参数极径极角(r,/O)表示.而对圆来说,我们需要三个参数来表示一个圆,也就是x,y是圆心位置,r是半径
霍夫梯度法的原理
霍夫梯度法的原理是这样的:
(1)首先对图像应用边缘检测,比如用canny边缘检测。
(2)然后,对边缘图像中的每一个非零点,考虑其局部梯度,即用Sobel()函数计算x和y方向的Sobel一阶导数得到梯度。
(3)利用得到的梯度,由斜率指定的直线上的每一个点都在累加器中被累加,这里的斜率是从一个指定的最小值到指定的最大值的距离。
(4)同时,标记边缘图像中每一个非0像素的位置。
(5)然后从二维累加器中这些点中选择候选的中心,这些中心都大于给定阈值并且大于其所有近邻。这些候选的中心按照累加值降序排列,以便于最支持像素的中心首先出现。
(6)接下來对每一个中心,考虑所有的非0像素。
(7)这些像索按照其与中心的距离棑序。从到最大半径的最小距离算起,选择非0像素最支持的一条半径。
(8)如果一个中心收到边缘阁像非0像素最充分的支持,并且到前期被选择的中心有足够的距离,那么它就会被保留下来。
这个实现可以使算法执行起来更卨效,或许更加重要的是,能够帮助解决三维累加器中会产生许多噪声并且使得结果不稳定的稀疏分布问题。
霍夫梯度法的缺点
(1)在霍夫梯度法中,我们使用Sobel导数来计算局部梯度,那么随之而来的假设是,它可以视作等同于一条局部切线,这并不是一个数值稳定的做法。在大多数情况下,这样做会得到正确的结果,但或许会在输出中产生一些噪声。
(2)在边缘图像中的整个非0像素集被看做毎个中心的候选部分。因此,如果把累加器的阈值设置偏低,算法将要消耗比较长的时间。此外,因为每一个中心只选择一个圆,如果有同心圆,就只能选择其中的一个。
(3)因为中心是按照其关联的累加器值的升序排列的,并且如果新的中心过于接近之前已经接受的中心的话,就不会被保留下来。且当有许多同心圆或者是近似的同心圆时,霍夫梯度法的倾向是保留最大的一个圆。可以说这是一种比较极端的做法,因为在这里默认Sobel导数会产生噪声,若是对于无穷分辨率的平滑图像而言的话,这才是必须的。
重映射
概念
重映射,就是把一幅图像中某位置的像素放置到另一个图片指定位位置的过程。为了完成映射过程,需要获得一些插值为非整数像素的坐标,因为源图像与目标图像的像素坐标不是一一对应的。一般惜况下,我们通过重映射来表达每个像素的位置(x,y),像这样:

在这里,g()是目标图像,们是源图像.而h(x,y)是作用f(x,y)的映射方法函数。
来看个例子。若有一幅图像1,对其按照下面的条件作重映射:
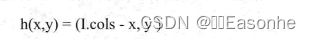
图像会按照x轴方向发生翻转。那么,源图像和效果图分别如图所示:

仿射变换
认识仿射变换
仿射变换(AffineTransformation或AffineMap),又称仿射映射,是指在几何中,一个向量空间进行一次线性变换并接上一个平移,变换为另一个向量空间的过程。它保持了二维图形的“平直性”(直线经过变换之后依然是直线)和“平行性”(二维图形之间的相对位置关系保持不变,平行线依然是平行线,且直线上点的位置顺序不变)。
一个任意的仿射变换都能表示为乘以一个矩阵(线性变换)接着再加上一个向量(平移)的形式。
那么,我们能够用仿射变换来表示如下三种常见的变换形式:
- 旋转,rotation(线性变换)
- 平移,translation(向量加)
- 缩放,scale(线性变换)
进行更深层次的理解,仿射变换代表的是两幅图之间的一种映射关系。而我们通常使用2x3的矩阵来表示仿射变换。

仿射变换的求法
我们知道,仿射变换表示的就是两幅图片之间的一种联系,关于这种联系的信息大致可从以下两种场景获得。
- 己知X和T,而且已知它们是有联系的。接下来的工作就是求出矩阵M。
- 已知M和X,想求得T。只要应用算式T=M-X即可。对于这种联系的信息可以用矩阵M清晰地表达(即给出明确的2x3矩阵),也可以用两幅图片点之间几何关系來表达。
形象地说明一下,因为矩阵M联系着两幅图片,就以其表示两图中各三点直接的联系为例。如图:
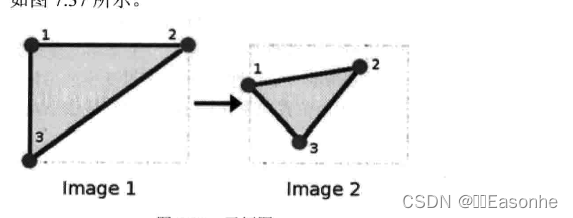
图中,点1、2和3(在Imagel中形成一个三角形)与Image2中的三个点是一一映射的关系,且它们仍然形成三角形,但形状已经和之前不一样了。我们能通过这样两组三点求出仿射变换(可以选择自己喜欢的点),接着就可以把仿射变换应用到图像中去。
直方图均衡化
很多时候,我们用相机拍摄的照片的效果往往会不尽人意。这时,可以对这些图像进行一些处理,来扩大图像的动态范围。这种情况下最常用到的技术就是直方图均衡化。未经均衡化的图片范例如图:
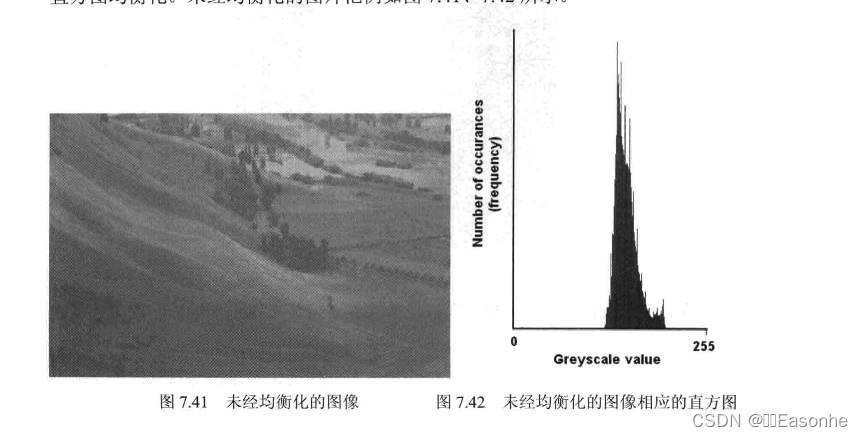
在图、中,我们可以看到,左边的图像比较淡,M为其数值范围变化比较小,可以在这幅图的直方图(图7.42)中明显地看到。因为处理的是8位图像,其亮度值是从0到255,但直方图值显示的实际亮度却集中在亮度范围的中问区域。为了解决这个问题,就可以用到直方图均衡化技术,先来看看其概念。
概念
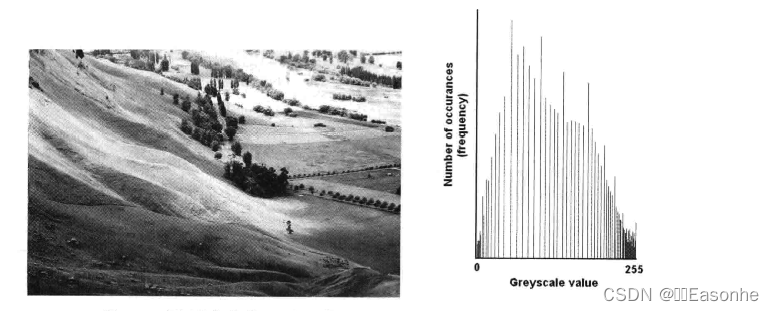
直方图均衡化是灰度变换的一个重要应用,它高效且易于实现,广泛应用于图像増强处理中。图像的像素灰度变化是随机的,直方图的图形高低不齐,直方图均衡化就是用一定的算法使直方图大致平和的方法。均衡化效果示例如图

简而言之,直方图均衡化是通过拉伸像素强度分布范围来增强图像对比度的一种方法。均衡化处理后的图像只能是近似均匀分布。均衡化图像的动态范围扩大了,似其本质是扩大了量化间隔,而量化级别反而减少了,因此,原来灰度不同的象素经处理后可能变的相同,形成了一片相同灰度的区域,各区域之间有明显的边界,从而出现了伪轮廓。在原始图像对比度本来就很高的情况卜,如果再均衡化则灰度调和,对比度会降低。在泛白缓和的图像中,均衡化会合并一些象素灰度,从而增大对比度。均衡化后的图片如果再对其均衡化,则图像不会有任何变化
end
这篇关于【计算机视觉】图像变换方法(边缘检测算子、霍夫变换、重映射、放射变换与直方图均衡化)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







