动态规划（算法竞赛、蓝桥杯）--状态压缩DP蒙德里安的梦想

本文主要是介绍动态规划（算法竞赛、蓝桥杯）--状态压缩DP蒙德里安的梦想，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1、B站视频链接：E31 状态压缩DP 蒙德里安的梦想_哔哩哔哩_bilibili

#include <bits/stdc++.h> 
using namespace std;
const int N=12,M=1<<N;
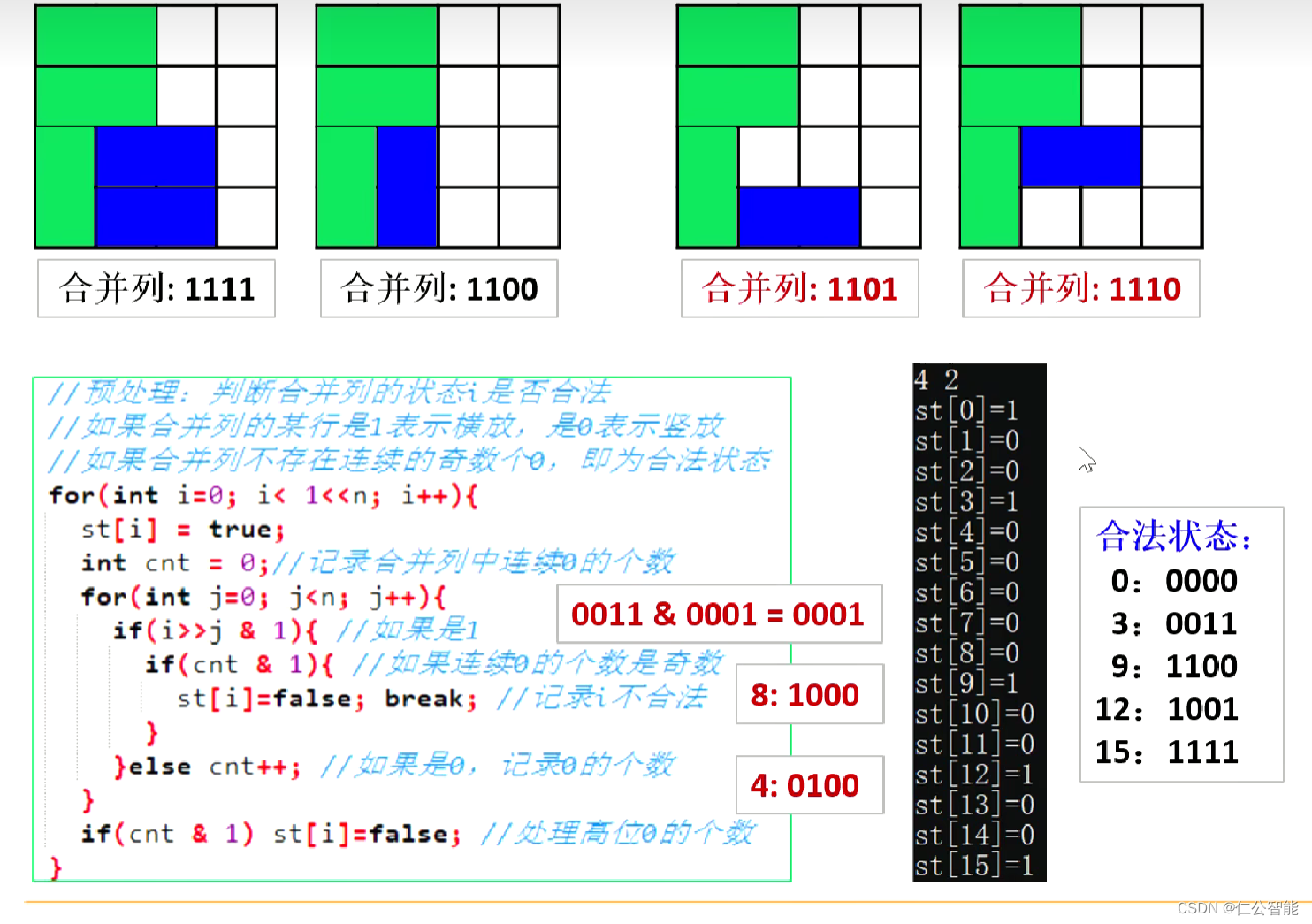
bool st[N];//st[i]存储合并列的状态i是否合法  
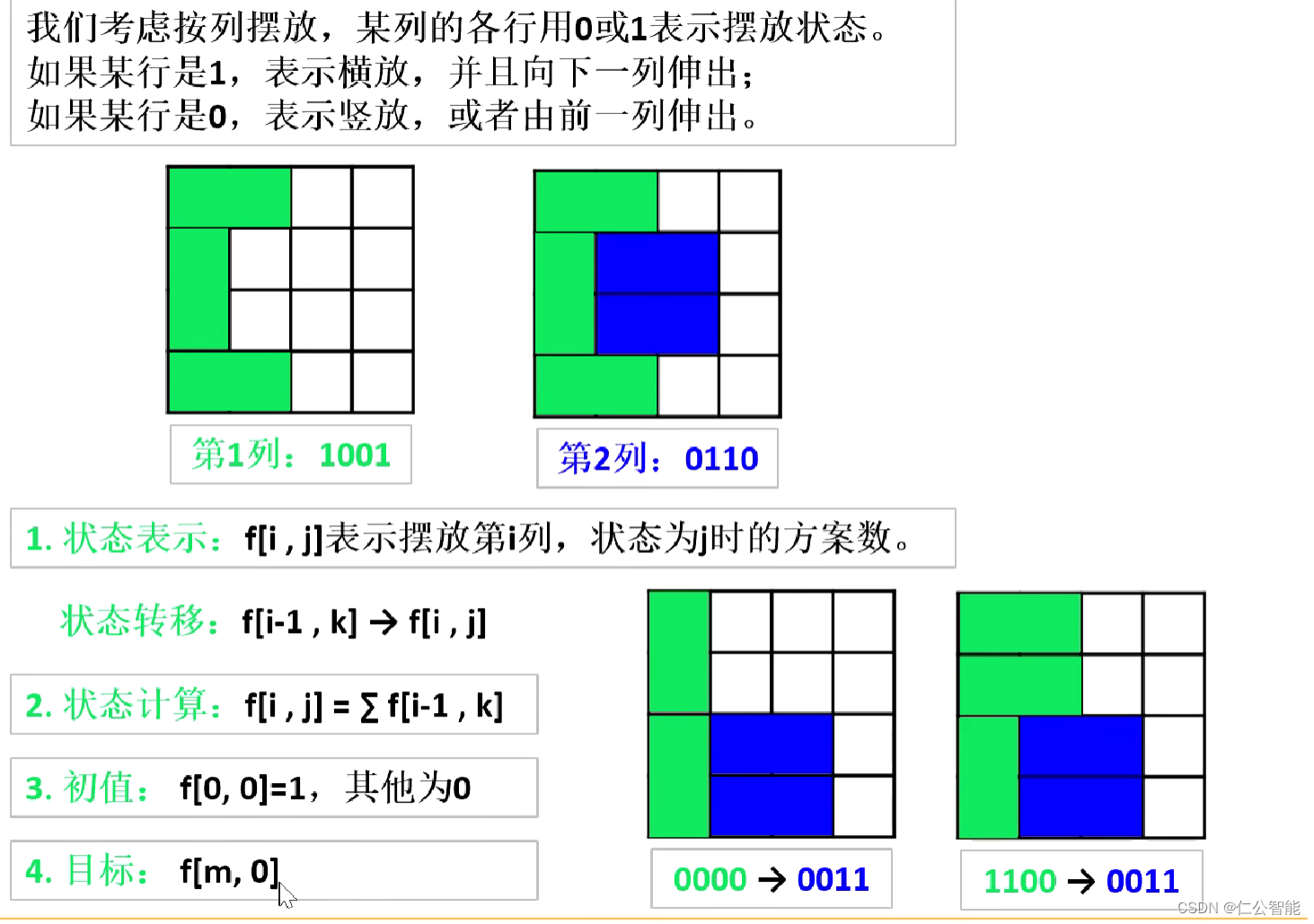
long long f[N][M];//f[i][j]表示摆放第i列，状态为j时的方案数 int main(){int n,m;while(cin>>n>>m,n||m){//预处理：判断合并列的状态i是否合法 //合并列即两列状态合并之意，对应后面的st[j|k]      //如果合并列的某行是1表示横放，是0表示竖放 //如果合并列不存在连续的奇数个0，即为合法状态 for(int i=0;i<1<<n;i++){//枚举状态 st[i]=true;int cnt=0; //记录合并列中连续0的个数 for(int j=0;j<n;j++){//n为行数，即状态的位数 if(i>>j&1){//如果i是1 if(cnt&1){//如果连续0的个数是奇数  st[i]=false;break;}}else{cnt++;//如果是0，记录0的个数 }}if(cnt&1)st[i]=false;//处理高位0的个数 }memset(f,0,sizeof f);f[0][0]=1;for(int i=1;i<=m;i++){//阶段：枚举列 for(int j=0;j<1<<n;j++){//状态：枚举第i列的状态 for(int k=0;k<1<<n;k++){//状态：枚举第i-1列的状态 if((j&k)==0&&st[j|k]){//两列状态兼容：不出现重叠的1，不出现连续的奇数个0 f[i][j]+=f[i-1][k];}}}}    printf("%lld\n",f[m][0]);//第m列不横放即答案}return 0;}