[OpenGL] 水面波动场景模拟 - 基于Gerstnder波实现

【更新】我的新博客：www.ryuzhihao.cc，当然这个csdn博客也会更新

              本文在新博客中的链接：点击打开链接

1. 时间：2017/3/19、大三下学期

2. 参考文献：

[1] John Hany的博客：http://johnhany.net/2014/02/water-rendering-with-gerstner-wave/

[2] 论文：基于Gerstner波模型的海洋卷浪实时仿真(作者：黄威 同济大学)  

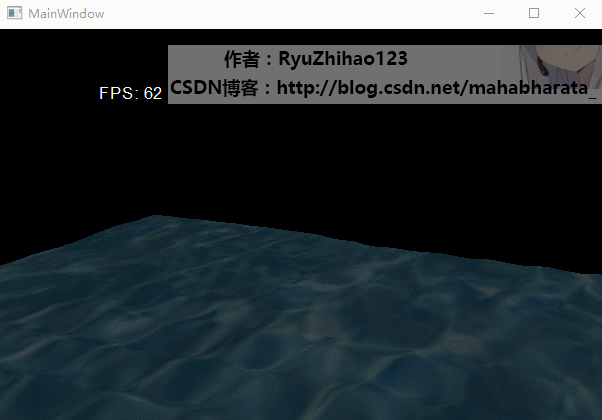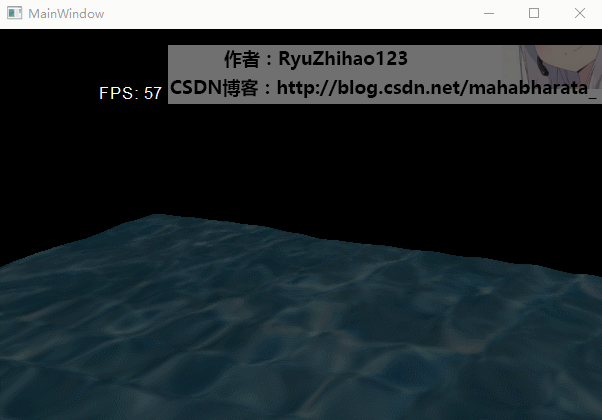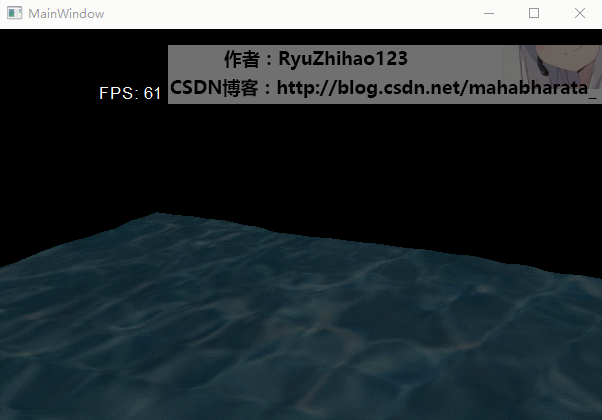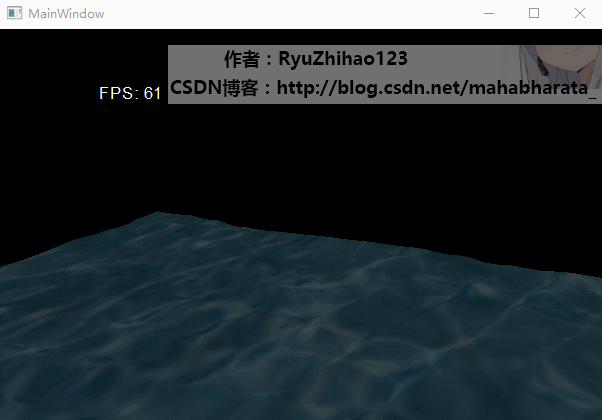
3. 首先给出我实现的效果：

4. 关于Gerstner波的基本原理：

        经典的Gerstner模型从动力学的角度描述了海浪各质点的运动.Gerstner波是最早的用于计算机图形学海浪仿真的方法,于1986年被Fournier首次引入计算机图形图像领域.

4.1 单个Gerstner波的数学模型：

                     
      上式为只考虑时刻t时单个波的情况。即：原质点为(x0,y0)，随着时间t，该点做波幅 r、波数k 、角频率w 的周期运动。

4.2 多个Gerstner叠加波的数学模型

而线性海浪理论认为,海浪是由多个不同波幅和不同角频率的波线性迭加而成.因此, 我们采用由上式得出的多个波的三维离散形式（不明白原理的，可以直接拿去用:-D）:
                          
       式中 ,定义xoz平面为水面静止时的平面,x轴正向朝右,z轴正向朝外,y轴为垂直方向,正向朝上,海面上的每一个点(x,y,z)都绕其静止时的位置(x0,y0,z0)作圆周运动.aij是组成波的波幅;ki是波数; ω i 是角频率,并在xoz水平面上沿x轴成θj角方向传播;n为频率的划分个数;m为方向的划分个数。

        令k=(ω×ω)/g （其中g=9.8为重力加速度）

5. 相关代码：

存储方式：使用顶点数组存储，并用三角网格绘制出来。

我设定的一组比较好用的参数：

    n = 3;  // 频率划分个数m = 2; // 方向的划分个数double _thetas[m] = {0.38,1.42};  // 传播方向double _amplitudes[n][m] ={  //波幅0.2,0.2,0.3,0.50,0.2,0.6,};double _omegas[n] = {3.27,3.31,3.42};     //  角频率double _ks[n] = {1.091,1.118,1.1935};  // 波数

定义一个方便计算的三维点类

class Point3
{
public:double x,y,z;Point3():x(0),y(0),z(0){}Point3(double x,double y,double z):x(x),y(y),z(z){}
};

Point3 Water::Gerstner(double x, double y, double z)
{for(int i=0; i<n; i++){for(int j=0; j<m; j++){x-= cos(thetas[j])*amplitudes[i][j]*sin(waveNums[i]*(x*cos(thetas[j])+z*sin(thetas[j]))-omegas[i]*time);y+= amplitudes[i][j]*cos(waveNums[i]*(x*cos(thetas[j])+z*sin(thetas[j]))-omegas[i]*time);z-= sin(thetas[j])*amplitudes[i][j]*sin(waveNums[i]*(x*cos(thetas[j])+z*sin(thetas[j]))-omegas[i]*time);}}return Point3(x,y,z);
}