week3-线性数据结构

P3613 【深基15.例2】寄包柜 

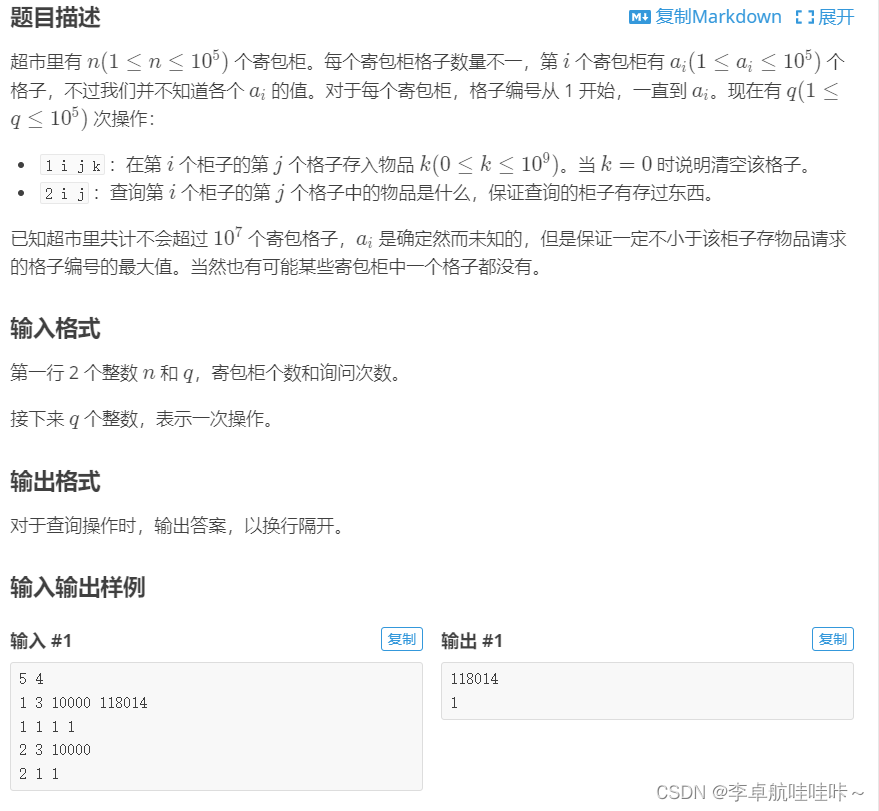
#include<iostream>
#include<map>
using namespace std;
int main() {int n,q;cin>>n>>q;map<pair<int,int>,int>mp;while(q--){int w;cin>>w;if(w==1){int i,j,k;cin>>i>>j>>k;mp[{i,j}]=k;}else if(w==2){int i,j;cin>>i>>j;cout<<mp[{i,j}]<<endl;}} return 0;
}

 map容器和pair容器的结合

P1241 括号序列

#include<iostream>
using namespace std;int a[10005];
char cha(char a){if(a==')')return '(';if(a==']')return '[';if(a=='(')return ')';if(a=='[')return ']';
}
int main()
{string s;cin>>s;for(int i=0;i<s.length();i++){if(s[i]==')'){for(int j=i-1;j>=0;j--){if(s[j]=='('&&a[j]!=1){a[i]=a[j]=1;break;}else if(s[j]=='['&&a[j]!=1)break;}}if(s[i]==']'){for(int j=i-1;j>=0;j--){if(s[j]=='['&&a[j]!=1){a[i]=a[j]=1;break;}else if(s[j]=='('&&a[j]!=1)break;}}}for(int i=0;i<s.length();i++){if(a[i]==0){if(s[i]==')')cout<<"()";if(s[i]==']')cout<<"[]";if(s[i]=='(')cout<<"()";if(s[i]=='[')cout<<"[]";}else cout<<s[i];}return 0;
}

题目理解：扫描一遍原序列，当找到一个右括号（即找到一个 ' ) ' 或者 ' ] ' 时），以它为起点向左找，找到一个没被标记成功匹配的左括号（即找到一个 ' ( ' 或者 ' [ ' ），如果两者匹配的话，标记它们成功匹配，如果不匹配，或者找不到左括号的话，不做任何标记。

P1449 后缀表达式

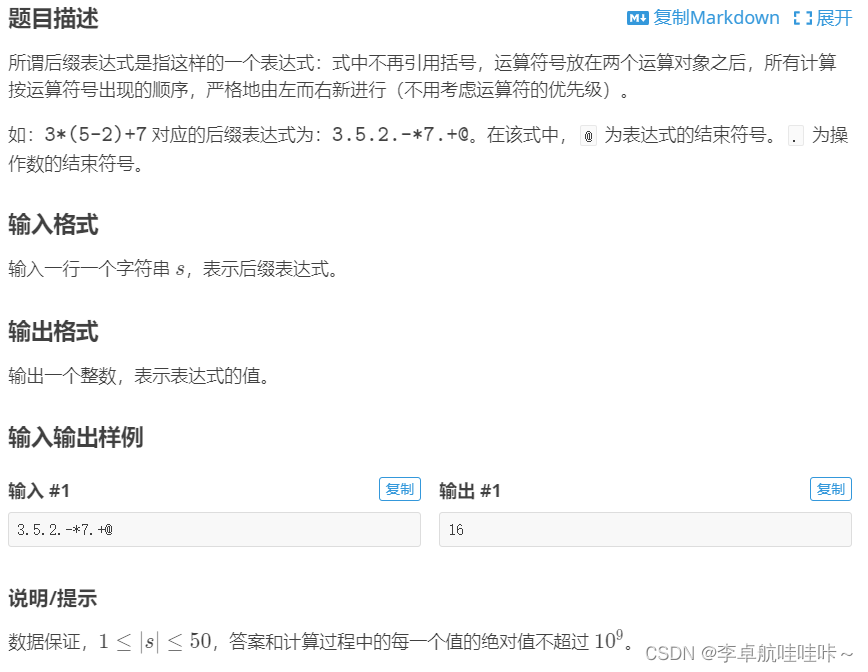
#include<iostream>
using namespace std;
const int maxn=55;
int arr[maxn],top=0;
int main(){char c;int n=0;int a=0,b=0;while((c=getchar())&&c!='@'){switch(c){case '*':a=arr[top];b=arr[top-1];top--;arr[top]=a*b;break;case '/':a=arr[top];b=arr[top-1];top--;arr[top]=b/a;break;case '+':a=arr[top];b=arr[top-1];top--;arr[top]=a+b;break;case '-':a=arr[top];b=arr[top-1];top--;arr[top]=b-a;break;case '.':arr[++top]=n;n=0;break;default:n=n*10+(c-'0');break;}}cout<<arr[top];return 0;
}

栈：（Stack）：是只允许在一端进行插入或删除的线性表。
栈顶（Top）：线性表允许进行插入删除的那一端。
栈底（Bottom）：固定的，不允许进行插入和删除的另一端。
空栈：不含任何元素的空表。 

主要使用语句：

P1160 队列安排 

#include <iostream>
using namespace std;
const int mx=1e5+5;
int m,n;
struct T{int past;int next;int d;
}a[mx]={0};
void charu(int i,int j,int f){if(f==1){//将j加入i的右边 a[j].next=a[i].next;//j右手牵i右手牵的同学 a[j].past=i;//j的左手牵i a[i].next=j;//i的右手牵j a[a[j].next].past=j;//j右手牵的同学的左手牵j }else if(f==0){//将j加入i的左边同理 a[j].next=i;a[j].past=a[i].past;a[i].past=j;a[a[j].past].next=j;}
}
int main() {cin>>n;int j,f;a[0].past=0;a[0].next=0;charu(0,1,1);for(int x=2;x<=n;x++){cin>>j>>f;charu(j,x,f);}cin>>m;while(m--){cin>>j;a[j].d=1;}for(int i=a[0].next;i;i=a[i].next){if(a[i].d==0)cout<<i<<" ";}return 0;
}

题解 P1160 【队列安排】 - BT狸——Frozen 的博客 - 洛谷博客

双向链表的使用