474 一零和

本文主要是介绍474 一零和，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目

给你一个二进制字符串数组 strs 和两个整数 m 和 n 。请你找出并返回 strs 的最大子集的长度，该子集中 最多 有 m 个 0 和 n 个 1 。如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集 。示例 1：输入：strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出：4
解释：最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ，因此答案是 4 。
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3 。
示例 2：输入：strs = ["10", "0", "1"], m = 1, n = 1
输出：2
解释：最大的子集是 {"0", "1"} ，所以答案是 2 。提示：1 <= strs.length <= 600
1 <= strs[i].length <= 100
strs[i] 仅由 '0' 和 '1' 组成
1 <= m, n <= 100

分析

此问题可以抽象成0-1背包问题，将每个字符串看做要放入背包中的物品即可，只不过比较特殊的是这个题目中的物品的重量有两个方向的考量，即0的个数和1的个数。以下为动规五部曲：

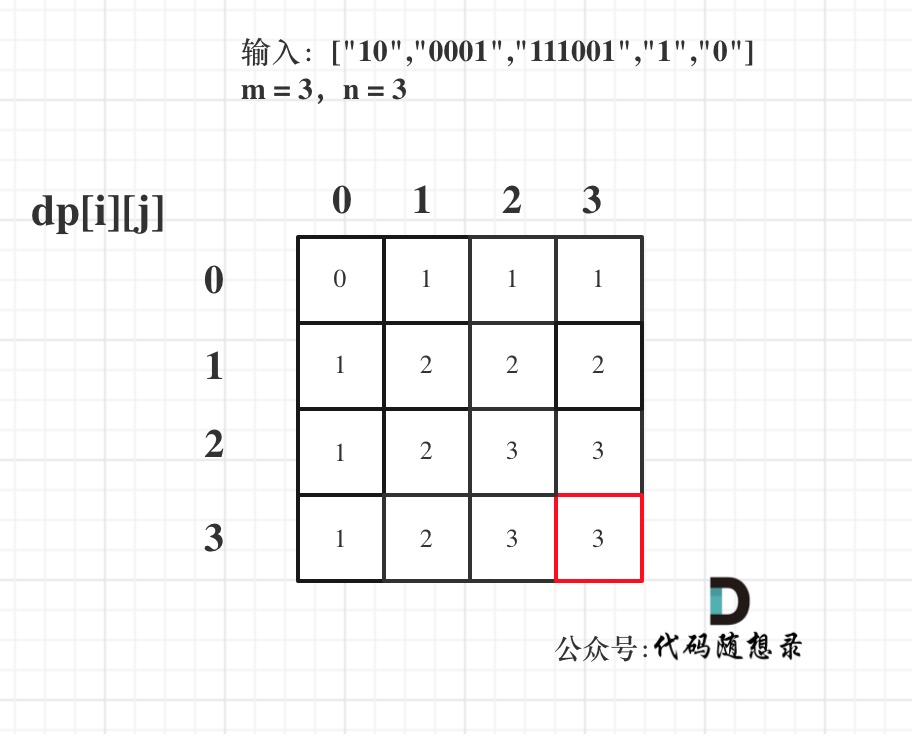
1、确定dp数组和下标含义：dp[i][j]当背包容量为i和j时，所能装入的字符串的最大个数
2、确定递推公式：dp[i][j] = max(dp[i][j],dp[i-zeroNum][j-oneNum]+1)，zeroNum表示0的个数，oneNum表示1的个数
3、dp数组初始化：初始化为0即可，这样可以避免正确的数值被初始化的数值覆盖
4、确定遍历顺序：先遍历物品，即字符串，再遍历背包
5、打印dp数组：出错或者不理解的话可以将dp数组打印出来看看

题解

题解一：

class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {vector<vector<int>> dp(m+1,vector<int>(n+1,0));for(string s:strs){//物品int oneNum = 0,zeroNum = 0;for(char c:s){//计算每个物品的重量if(c=='0')++zeroNum;else ++oneNum;}//背包for(int i = m;i>=zeroNum;--i){for(int j = n;j>=oneNum;--j){dp[i][j] = max(dp[i][j],dp[i-zeroNum][j-oneNum]+1);}}}return dp[m][n];}
};

题解二：

#include<iostream> 
#include<string>
#include<vector>
#include<algorithm>
using namespace std;int findMaxForm(vector<string>& strs, int m, int n) {vector<vector<int>> dp(m+1,vector<int>(n+1,0));for(string s:strs){int oneNum = 0,zeroNum = 0;for(char c:s){if(c=='0')++zeroNum;else ++oneNum;}for(int i = m;i>=zeroNum;--i){for(int j = n;j>=oneNum;--j){dp[i][j] = max(dp[i][j],dp[i-zeroNum][j-oneNum]+1);}}}return dp[m][n];
}int main(){ int num;cin>>num;vector<string> strs(num+1);for(int i = 0;i<num;++i){cin>>strs[i];}int m,n;cin>>m>>n;    int result = findMaxForm(strs, m, n);cout << result << endl;return 0;
}

这篇关于474 一零和的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---