474.一和零

2024-09-03 11:52

文章标签 474

本文主要是介绍474.一和零，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

474.一和零

给你一个二进制字符串数组 strs 和两个整数 m 和 n 。

请你找出并返回 strs 的最大子集的长度，该子集中最多有 m 个 0 和 n 个 1 。

如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的子集。

示例 1：

输入：strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出：4
解释：最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ，因此答案是 4 。
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3 。

示例 2：

输入：strs = ["10", "0", "1"], m = 1, n = 1
输出：2
解释：最大的子集是 {"0", "1"} ，所以答案是 2 。

思路

动态规划的题完全没思路。

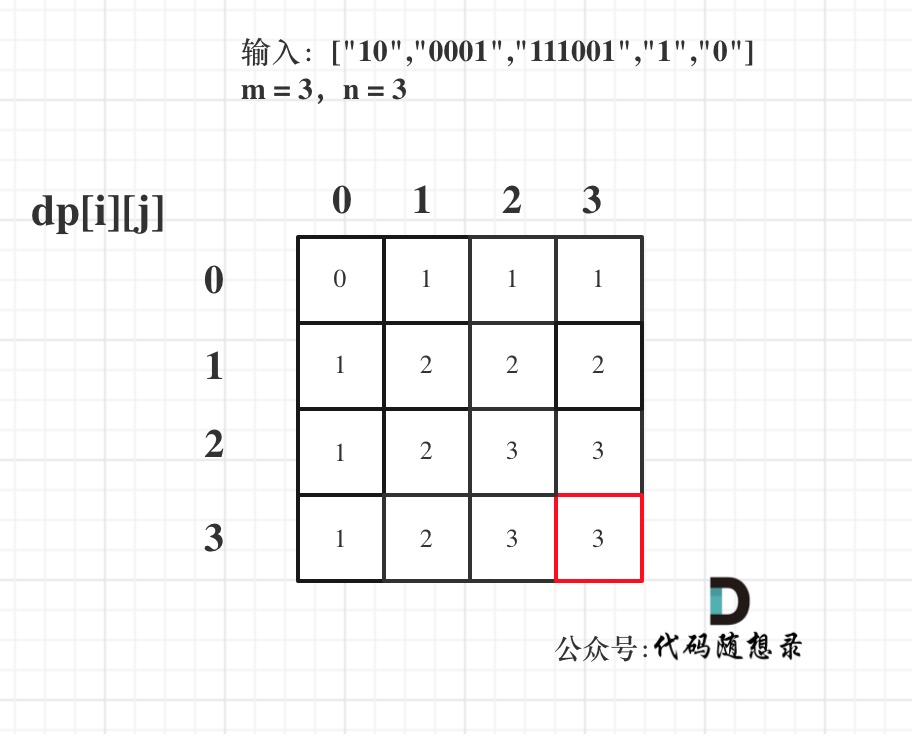
题解，将dp设为一个二维数组代表1和0两个容量下最大子串数量。初始化为0.遍历顺序上，顺序遍历子串（物品），逆序遍历背包容量，递推公式就是dp[i][j]=Math.max(dp[i][j],dp[i-zeroNum][j-oneNum]+1);这里类似于01背包问题，若当前子串（物品）的重量超过背包容量，无法进入循环，进入循环后递推公式有两种情况：1.不装当前子串能去最大2.装入当前子串能取最大。

这么理解下来题目还算透彻。

代码

  public int findMaxForm(String[] strs, int m, int n) {int[][] dp=new int[m+1][n+1];int oneNum,zeroNum;for (String str:strs){oneNum=0;zeroNum=0;for (int i=0;i<str.length();i++){if (str.charAt(i)=='0') oneNum++;else zeroNum++;}for (int i=m;i>=zeroNum;i--){for (int j=n;j>=oneNum;j--){dp[i][j]=Math.max(dp[i][j],dp[i-zeroNum][j-oneNum]+1);}}}return dp[m][n];}