由黑塞(Hessian)矩阵引发的关于正定矩阵的思考

最近看论文，发现论文中有通过黑塞(Hessian)矩阵提高电驱系统稳定性的应用。所以本篇主要从Hessian矩阵的性质出发，对其中正定矩阵的判定所引发的想法进行记录。

(其实看论文出现黑塞很惊奇，因为前不久刚读了作家黑塞的《德米安：彷徨少年时》，所以在这一领域的黑塞也做个记录吧。。)

首先，我理解的Hessian矩阵是对一个多元函数求最优的方法，百度百科上这样记载的：

图1 百度百科上关于Hessian矩阵的表述图

我们最关注的是求极小值求最优的问题，所以，对正定矩阵的判定是一个重点。

我们已知的“如何判定一个矩阵为正定矩阵？”有以下几点：

1. 矩阵特征值均大于0；

2. 各阶行列主子式均大于0；

3. 主元(pivots)均大于0，其中主元的乘积就是行列式的值；

4. 二次型恒大于0。

前三点都比较容易理解，问题就是计算量大。我们重点关注第四点，举个例子：(来源MIT 18.06 linear algebra)

矩阵A表示为：

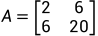
其二次型表示为：

现在问题转化成了，“如何判定这个二次型恒为正呢？”有以下几点：

1. 一阶导数=0，二阶导数>0；

2. 配方，>0；

3. 矩阵A正定，其二次型恒为正(这。。世界是一个圆嘛。。)

联系起来，其实质就是：

1. 特征向量表明主轴的方向，特征值表明轴的长度，>0正方向走，<0反方向走；

2. 求二阶导数大于0就等价于在求行列式的值大于0；

3. 配方就是在消元，即求A的LU分解，配方项前的系数2、2，就是主元大于0。

最后总结一下：用空间力来想，看下图，在一个xyz的三维空间内，令z=1即上述二次型式子=1。如果横切后得到的是椭圆，即函数在空间上为一个开口向上的碗状，则证明二次型存在极小值且矩阵正定；如果横切后得到的是双曲线，即函数在空间上为马鞍形，则证明二次型存在鞍点但不存在极小值点且矩阵不是正定的。这也就是为什么说：

椭圆与正定相关，双曲线与正定无关。

同样的，扩展到四维，切出来的三次型就是一个三维橄榄球了。。

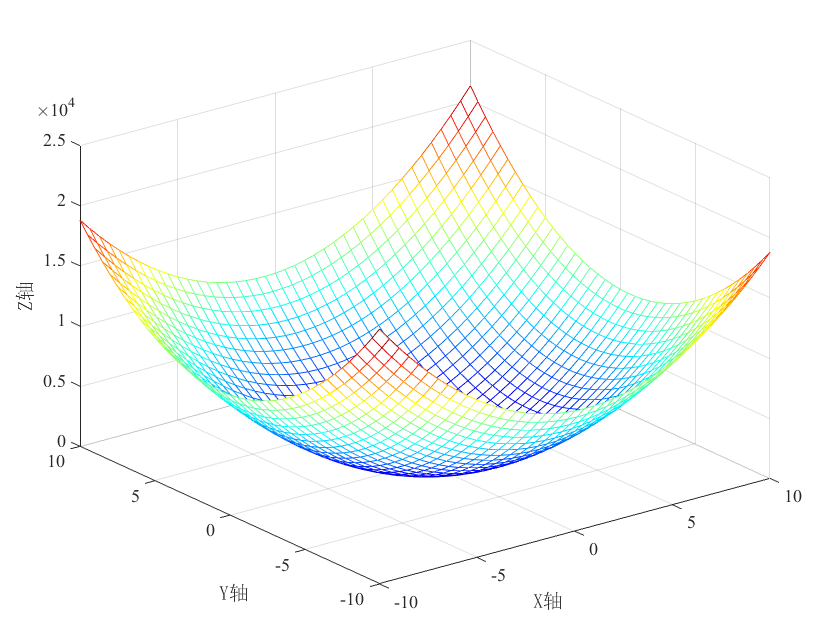为了便于观察，所绘制三维图与例子里的非同一函数

如果此篇文章对您有帮助，记得评论区告诉我: )

您的点赞和收藏是对写作者最大的鼓励！