数据结构之霍夫曼树

计算机里每个字符在没有压缩的文本文件中都由一个字节（如ASCII码）或两个字节（如Unicode码）表示。这些方案中，每个字符需要相同的位数

下表列出了字母对应的ASCII码

字母            十进制                二进制

A                  65                 01000001

B                  66                 01000010

C                  67                 01000011

……

X                  88                 01011000

Y                  89                 01011001

Z                  90                 01011010

在英文中，字母E的使用频率最高，而字母Z的使用频率最低，但是，无论使用频率高低，我们一律使用相同位数的编码来存储，是不是有些浪费空间呢？试想，如果我们对使用频率高的字母用较少的位数来存储，而对使用频率低的字母用较多的位数来存储，会大大提升存储效率

霍夫曼编码就是根据以上的设想来处理数据压缩的

例如，我们要发送一句消息：

SUSIE SAYS IT IS EASY

统计所有符号出现的频率：

换行符        1次

T                  1次

U                  1次

A                  2次

E                  2次

Y                  2次

I                   3次

空格            4次

S                  6次

S出现的频率最多，我们可以将它的编码设为10，其次是空格，我们将它设置为00，接下来的编码必须增加位数了。三位码我们有八种选择：000,001,010,011,100,101,110,111。但是，以10或00开头的是不能使用的，只能从010,011,110,111中选择。因为如果我们用101表示I，用010表示Y，101010既可以分解为101,010两个有意义的编码，也能分解为10,10,10三个有意义的编码，这显然是不允许的。我们必须保证，任何信息编码之后，解码时都不会出现歧义。借助霍夫曼树就能便捷的实现编码

霍夫曼树是最优二叉树。树的带权路径长度规定为所有叶子结点的带权路径长度之和，带权路径长度最短的树，即为最优二叉树。在最优二叉树中，权值较大的结点离根较近。

首先就需要构建一个霍夫曼树，一般利用优先级队列来构建霍夫曼树

以上面的消息为例，我们先来分析一下构建霍夫曼树的过程，下图中，if代表换行符，sp代表空格

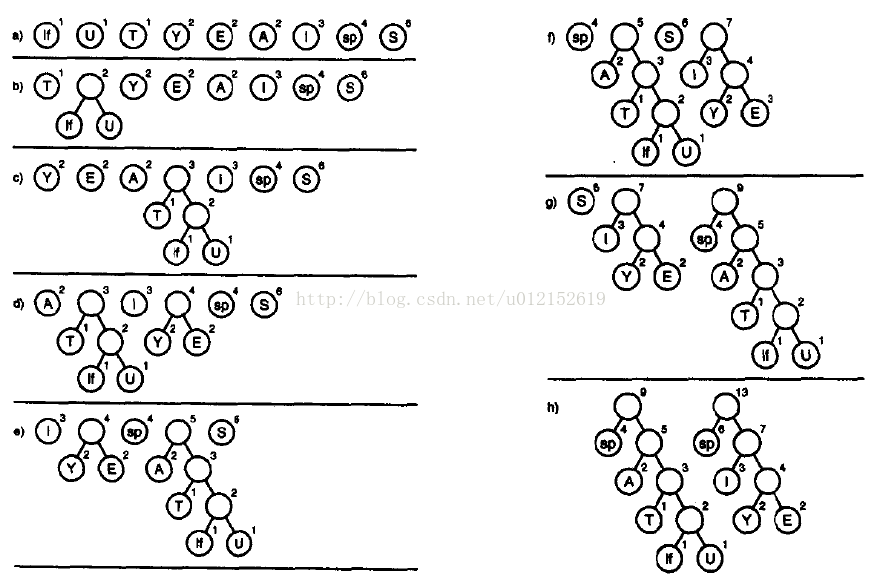
首先，将字符按照频率插入一个优先级队列，频率越低越靠近队头，然后循环执行下面的操作：

1、取出队头的两个树

2、以它们为左右子节点构建一棵新树，新树的权值是两者之和

3、将这棵新树插入队列

直到队列中只有一棵树时，这棵树就是我们需要的霍夫曼树

接下来我们用Java来实现上面的过程，代码如下：

[java]  view plain copy

print ?

1. //节点类  
2. public class Node{  
3.       private String key;           //树节点存储的关键字，如果是非叶子节点为空  
4.       private int frequency;        //关键字词频  
5.       private Node left;            //左子节点  
6.       private Node right;           //右子节点  
7.       private Node next;            //优先级队列中指向下一个节点的引用  
8.        
9.       public Node(int fre,String str){  //构造方法1  
10.              frequency = fre;  
11.              key = str;  
12.       }  
13.       public Node(int fre){  //构造方法2  
14.              frequency = fre;  
15.       }  
16.        
17.       public String getKey() {  
18.              return key;  
19.       }  
20.       public void setKey(String key) {  
21.              this.key = key;  
22.       }  
23.       public Node getLeft() {  
24.              return left;  
25.       }  
26.       public void setLeft(Node left) {  
27.              this.left = left;  
28.       }  
29.       public Node getRight() {  
30.              return right;  
31.       }  
32.       public void setRight(Node right) {  
33.              this.right = right;  
34.       }  
35.       public Node getNext() {  
36.              return next;  
37.       }  
38.       public void setNext(Node next) {  
39.              this.next = next;  
40.       }  
41.       public int getFrequency() {  
42.              return frequency;  
43.       }  
44.       public void setFrequency(int frequency) {  
45.              this.frequency = frequency;  
46.       }  
47. }  

[java]  view plain copy

print ?

1. //用于辅助创建霍夫曼树的优先级队列  
2. public class PriorityQueue{  
3.       private Node first;  
4.       private int length;  
5.        
6.       public PriorityQueue(){  
7.              length = 0;  
8.              first = null;  
9.       }  
10.        
11.       //插入节点  
12.       public void insert(Node node){  
13.              if(first == null){  //队列为空  
14.                     first = node;  
15.              }else{  
16.                     Node cur = first;  
17.                     Node previous = null;  
18.                     while(cur.getFrequency()< node.getFrequency()){  //定位要插入位置的前一个节点和后一个节点  
19.                            previous = cur;  
20.                            if(cur.getNext() ==null){  //已到达队尾  
21.                                   cur = null;  
22.                                   break;  
23.                            }else{  
24.                                   cur =cur.getNext();  
25.                            }  
26.                             
27.                     }  
28.                     if(previous == null){  //要插入第一个节点之前  
29.                            node.setNext(first);  
30.                            first = node;  
31.                     }else if(cur == null){  //要插入最后一个节点之后  
32.                            previous.setNext(node);  
33.                     }else{  //插入到两个节点之间  
34.                            previous.setNext(node);  
35.                            node.setNext(cur);  
36.                     }  
37.              }  
38.              length++;  
39.       }  
40.        
41.       //删除队头元素  
42.       public Node delete(){  
43.              Node temp = first;  
44.              first = first.getNext();  
45.              length--;  
46.              return temp;  
47.       }  
48.        
49.       //获取队列长度  
50.       public int getLength(){  
51.              return length;  
52.       }  
53.        
54.       //按顺序打印队列  
55.       public void display(){  
56.              Node cur = first;  
57.              System.out.print("优先级队列：\t");  
58.              while(cur != null){  
59.                     System.out.print(cur.getKey()+":"+cur.getFrequency()+"\t");  
60.                     cur = cur.getNext();  
61.              }  
62.              System.out.println();  
63.       }  
64.        
65.       //构造霍夫曼树  
66.       public HuffmanTree buildHuffmanTree(){  
67.              while(length > 1){  
68.                     Node hLeft = delete();  //取出队列的第一个节点作为新节点的左子节点  
69.                     Node hRight = delete(); //取出队列的第二个节点作为新节点的右子节点  
70.                     //新节点的权值等于左右子节点的权值之和  
71.                     Node hRoot = new Node(hLeft.getFrequency()+hRight.getFrequency());  
72.                     hRoot.setLeft(hLeft);  
73.                     hRoot.setRight(hRight);  
74.                     insert(hRoot);  
75.              }  
76.              //最后队列中只剩一个节点，即为霍夫曼树的根节点  
77.              return new HuffmanTree(first);  
78.       }  
79.        
80. }  

 

[java]  view plain copy

print ?

1. import java.util.HashMap;  
2. import java.util.Map;  
3. //霍夫曼树类  
4. public class HuffmanTree {  
5.       private Node root;  
6.       private Map codeSet = new HashMap();  //该霍夫曼树对应的字符编码集  
7.        
8.       public HuffmanTree(Node root){  
9.              this.root = root;  
10.              buildCodeSet(root,"");  //初始化编码集  
11.       }  
12.        
13.       //生成编码集的私有方法，运用了迭代的思想  
14.       //参数currentNode表示当前节点，参数currentCode代表当前节点对应的代码  
15.       private void buildCodeSet(NodecurrentNode,String currentCode){  
16.              if(currentNode.getKey() != null){  
17.                     //霍夫曼树中，如果当前节点包含关键字，则该节点肯定是叶子节点，将该关键字和代码放入代码集  
18.                     codeSet.put(currentNode.getKey(),currentCode);  
19.              }else{//如果不是叶子节点，必定同时包含左右子节点，这种节点没有对应关键字  
20.                     //转向左子节点需要将当前代码追加0  
21.                     buildCodeSet(currentNode.getLeft(),currentCode+"0");  
22.                     //转向右子节点需要将当前代码追加1  
23.                     buildCodeSet(currentNode.getRight(),currentCode+"1");  
24.              }  
25.       }  
26.        
27.       //获取编码集  
28.       public Map getCodeSet(){  
29.              return codeSet;  
30.       }  
31.        
32. }  

 

[java]  view plain copy

print ?

1. //测试类  
2. public static void main(String[] args) throws Exception{  
3.              PriorityQueue queue = new PriorityQueue();  
4.              Node n1 = new Node(1,"if");  
5.              Node n2 = new Node(1,"U");  
6.              Node n3 = new Node(1,"T");  
7.              Node n4 = new Node(2,"Y");  
8.              Node n5 = new Node(2,"E");  
9.              Node n6 = new Node(2,"A");  
10.              Node n7 = new Node(3,"I");  
11.              Node n8 = new Node(4,"sp");  
12.              Node n9 = new Node(5,"S");  
13.              queue.insert(n3);  
14.              queue.insert(n2);  
15.              queue.insert(n1);  
16.              queue.insert(n6);  
17.              queue.insert(n5);  
18.              queue.insert(n4);  
19.              queue.insert(n7);  
20.              queue.insert(n8);  
21.              queue.insert(n9);  
22.              queue.display();  
23.               
24.              HuffmanTree tree =queue.buildHuffmanTree();  
25.              Map map = tree.getCodeSet();  
26.              Iterator it =map.entrySet().iterator();  
27.              System.out.println("霍夫曼编码结果：");  
28.              while(it.hasNext()){  
29.                     Entry<String,String>entry = (Entry)it.next();  
30.                     System.out.println(entry.getKey()+"——>"+entry.getValue());  
31.              }  
32.       }  

控制台打印结果如下图所示：

可见，达到了预期的效果

秉承没有最好，只有更好的精神，我们不应该就此止步。现在我们做到的只是得到某个字符对应的霍夫曼编码，但是这个字符的词频仍然需要我们手工去统计、输入，更深入的思考一下，能不能更智能化一点，只要我们输入完整的一段消息，就能给出对应的霍夫曼编码，而且能对编码进行解码呢？

显然是可以的，先面就让我们用神奇的java语言来对上面的底层操作进行更高级的封装，来达到预期的功能

就是说，我们要利用上面已经写出的代码来封装一个编码类，这个类的一个方法接受一个字符串消息，返回霍夫曼编码，此外，还有一个解码类，接受一段完整的霍夫曼编码，返回解码后的消息内容。这实际上就是压缩与解压的模拟过程

[java]  view plain copy

print ?

1. import java.util.HashMap;  
2. import java.util.Iterator;  
3. import java.util.Map;  
4. import java.util.Map.Entry;  
5.    
6. //霍夫曼编码器  
7. public class HuffmanEncoder {  
8.       private PriorityQueue queue;       //辅助建立霍夫曼树的优先级队列  
9.       private HuffmanTree tree;         //霍夫曼树  
10.       private String [] message;            //以数组的形式存储消息文本  
11.       private Map keyMap;                            //存储字符以及词频的对应关系  
12.       private Map codeSet;                     //存储字符以及代码的对应关系  
13.        
14.       public HuffmanEncoder(){  
15.              queue = new PriorityQueue();  
16.              keyMap = new HashMap<String,Integer>();  
17.       }  
18.        
19.       //获取指定字符串的霍夫曼编码  
20.       public String encode(String msg){  
21.              resolveMassage(msg);  
22.              buildCodeSet();  
23.              String code = "";  
24.              for(inti=0;i<message.length;i++){//将消息文本的逐个字符翻译成霍夫曼编码  
25.                     code =code+codeSet.get(message[i]);  
26.              }  
27.              return code;  
28.       }  
29.        
30.       //将一段字符串消息解析成单个字符与该字符词频的对应关系，存入Map  
31.       private void resolveMassage(String msg){  
32.               
33.              char [] chars =msg.toCharArray();  //将消息转换成字符数组  
34.              message = new String[chars.length];  
35.              for(int i =0;i<chars.length;i++){  
36.                     String key = "";  
37.                     key =chars[i]+"";  //将当前字符转换成字符串  
38.                      
39.                     message [i] =  key;  
40.                     if(keyMap.containsKey(key)){//如果Map中已存在该字符，则词频加一  
41.                            keyMap.put(key,(Integer)keyMap.get(key)+1);  
42.                     }else{//如果Map中没有该字符，加入Map  
43.                            keyMap.put(key,1);  
44.                     }  
45.              }  
46.       }  
47.        
48.       //建立对应某段消息的代码集  
49.       private void buildCodeSet(){  
50.              Iterator it =keyMap.entrySet().iterator();  
51.              while(it.hasNext()){  
52.                     Entry entry =(Entry)it.next();  
53.                     //用该字符和该字符的词频为参数，建立一个新的节点，插入优先级队列  
54.                     queue.insert(new Node((Integer)entry.getValue(),(String)entry.getKey()));  
55.              }  
56.              queue.display();  
57.              tree =queue.buildHuffmanTree();  //利用优先级队列生成霍夫曼树  
58.              codeSet = tree.getCodeSet();   //获取霍夫曼树对应的代码集  
59.       }  
60.        
61.       //打印该段消息的代码集  
62.       public void printCodeSet(){  
63.              Iterator it =codeSet.entrySet().iterator();  
64.              System.out.println("代码集：");  
65.              while(it.hasNext()){  
66.                     Entry entry =(Entry)it.next();  
67.                     System.out.println(entry.getKey()+"——>"+entry.getValue());  
68.              }  
69.              System.out.println();  
70.       }  
71.        
72.       //获取该段消息的代码集  
73.       public Map getCodeSet(){  
74.              return codeSet;  
75.       }  
76. }  

 

[java]  view plain copy

print ?

1. import java.util.Iterator;  
2. import java.util.Map;  
3. import java.util.Map.Entry;  
4.    
5. //霍夫曼解码器  
6. public class HuffmanDecoder {  
7.       private Map codeSet;  //代码段对应的代码集  
8.        
9.       public HuffmanDecoder(Map map){  
10.              codeSet = map;  
11.       }  
12.        
13.       //将代码段解析成消息文本  
14.       public String decode(String code){  
15.              String message = "";  
16.              String key = "";  
17.              char [] chars = code.toCharArray();  
18.              for(int i=0;i<chars.length;i++){  
19.                     key += chars[i];  
20.                     if(codeSet.containsValue(key)){  //代码集中存在该段代码  
21.                            Iterator it =codeSet.entrySet().iterator();  
22.                            while(it.hasNext()){  
23.                                   Entry entry = (Entry)it.next();  
24.                                   if(entry.getValue().equals(key)){  
25.                                          message+= entry.getKey();  //获取该段代码对应的键值，即消息字符  
26.                                   }  
27.                            }  
28.                            key ="";  //代码段变量置为0  
29.                     }else{  
30.                            continue;  //该段代码不能解析为文本消息，继续循环  
31.                     }  
32.              }  
33.              return message;  
34.       }  
35. }  

 

[java]  view plain copy

print ?

1. //测试类  
2. public static void main(String[] args){  
3.               
4.              String message = "chen long fei is hero !";  
5.              HuffmanEncoder encoder = new HuffmanEncoder();  
6.              String code =encoder.encode(message);  
7.               
8.              encoder.printCodeSet();  
9.              System.out.print("编码结果：");  
10.              System.out.println(code);  
11.               
12.              HuffmanDecoder decoder = new HuffmanDecoder(encoder.getCodeSet());  
13.              String message2 =decoder.decode(code);  
14.              System.out.print("解码结果：");  
15.              System.out.println(message);  
16.       }  

运行结果如下图所示：