本文主要是介绍手推支持向量机01-硬间隔SVM-模型定义(最大间隔分类器),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
1.写在前面
2.硬间隔SVM(hard-margin SVM)
1.写在前面
支持向量机SVM是机器学习中非常流行的分类算法,最近朋友推荐了机器学习-白板推导系列(六)-支持向量机SVM(Support Vector Machine)视频,感觉这个大佬讲的非常棒,之前写的关于svm的东西太浅显了,于是重新整理,方便以后复习。我们主要是从理论推导SVM是怎么一步一步演化到一个优化问题。从核心概念上讲,有一个口头禅:SVM有三宝,间隔、对偶、核技巧。
首先核技巧和svm没有一个具体的绑定关系,在svm之前核函数已经有一套单独的理论体系了,只不过是核技巧能够让svm从普通特征空间映射到高维空间,可以实现一定的非线性分类。
从类别上我们可以分为硬间隔SVM(hard-margin SVM)、软间隔SVM(soft-margin SVM)、kernel SVM。根据不同的情况我们使用不同的SVM算法。我们首先讲一下最基础的硬间隔SVM(hard-margin SVM)。
2.硬间隔SVM(hard-margin SVM)
我们先从几何角度上看待SVM算法,首先SVM首次提出是为了解决二分类问题的,比如我们可以画一个平面,横纵坐标为x1,x2。我们在图中表示两个类别,一般情况下,我们需要找到一个线,让这两个类别正确的分割开。我们定义这个线是一个超平面,那么我们模型可以表示为
,sign是一个符号函数,当后面大于0时,属于+1;当后面小于等于0时,属于-1。所以SVM本质上是一个纯粹的判别模型,跟概率没有关系。
我们可以知道能够正确把+1和-1分开的线是有好多条,可以说是有无数条的。我们在感知机学习算法PLA(Percetron Learning Algorithm)中根据初始值不同可以找到对应的超平面,从而将分类问题解决掉。这个SVM到底有什么特别之处呢?我们知道有那么多条可以分类的直线,哪一条才是最好的呢?SVM从几何意义上讲就是从这么多可以正确分类的超平面之中找到最好的一个。因为我们机器学习算法不仅仅要关注训练误差,我们更要关注期望损失,或者说测试误差。

假设我们找到上面这样一条线,它的鲁棒性是非常差的,也就是说这条直线对于噪声是非常的敏感。加入有一个样本在直线附近,很大概率出现误判,所以其泛化误差是非常差的。这个就是我们的出发点,找到最中间的一条超平面,让它离样本点都足够的大。
硬间隔SVM,别称是最大间隔分类器。我们从这几个字出发,用数学语言将刚才几何意义表达出来。最大我们用max表示,间隔我们用margin表示,w,t都是相关的,样本点用这样表示: ,约束条件st满足:

对于上面这个公式,我们可以进一步写做下面形式,同时我们最大间隔分类器通过数学语言表达出来了:
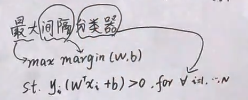
下面我们看一下我们自己定义的间隔margin函数,我们把margin定义为样本点到超平面的最小距离distance。从N个样本distance里面,找到最小的那个distance。点到直线距离,我们重新复习一下:
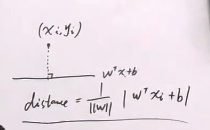
这样的话,margin和max margin就可以表示为:

因为>0,所以上面
中绝对值可以去掉。变成了下面形式:

我们继续观察上面的式子,我们知道min是和Xi相关,和w是没有关系的。所以我们可以把w往前提,得到下面的式子:

我们继续观察我们的约束st:>0,可以讲一定存在一个 r>0,使得最小的
=r。并且把上面公式中替换成r。
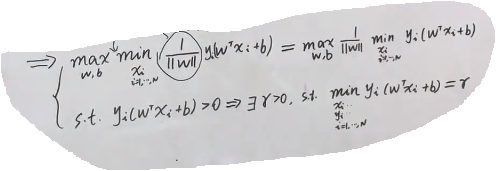
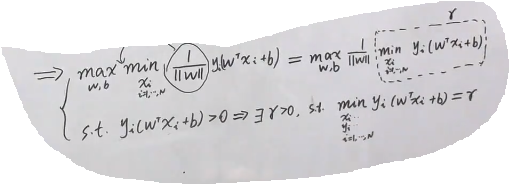
而且,这个 r 我们可以定义为1,其实是为了简化运算。为什么是可行的呢?这个是函数间隔和几何间隔的问题,是那个超平面,如果同时将w和b放大2倍,
,它们指的是同一个超平面。比如我们规定x的范数
=1,2或者100,就是将它固定下来,这样我们指定一个超平面
的时候,值是能够确定下来的。不然这个值是有无穷多的,因为可以随意缩放。r是一个大于0的数子,我们可以以任意比例缩放为1,对整个等式是没有影响的,仅仅为了简化运算。而且最大化可以转化为最小化。
我们整个式子可以简化为:
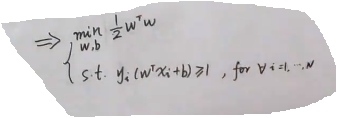
所以硬间隔SVM最后转化为了上面一个优化问题,并且是一个凸优化的问题。一共有N个约束,目标函数是二次的。整个几何意义转化为了凸优化问题,关于求解整个公式,我们会单独分析。如果样本数目不多,维数不多,就是一个简单的QP问题(二次规划问题),直接利用套件求解,如果复杂的话,需要引入对偶和kernel方法,用来求解该优化问题。
这篇关于手推支持向量机01-硬间隔SVM-模型定义(最大间隔分类器)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






